初中數學教學中培養學生探究性學習初探

王振國

《數學課程標準》指出：“動手實踐、自主探索與合作交流是學生學習數學的重要方式”。學生的創新意識是在主動探索知識的過程中得到培養的，學生的實踐能力是在運用知識解決問題的實踐活動中得以形成和發展的，課堂是培養學生創新意識和實踐能力的主陣地。因此，進行初中數學探究性學習的課堂教學實踐，尋找與時代發展相適應的教學方式方法十分重要。所謂探究性學習，是指在教師的組織和指導下，學生在數學學習情境中，主動觀察事物，發現問題，提出假設或猜想，又經過調查、實驗、搜集資料、建立模型，然后進行分析、思考、表達與交流的過程。下面結合本人在初中數學教學中引導培養學生進行探究性學習的幾點做法和思考總結如下：

一、在概念的形成過程中進行探究性學習

概念的形成是一個從具體到抽象的過程，學生獲得概念的過程，是一個抽象概括的過程。對抽象數學概念的教學，更要關注概念的實際背景，從形象出發，讓學生切實參與概念的形成過程，讓學生通過體驗一些熟知的實例進一步得到思考，得出結論，形成概念。例如在函數概念教學中，一開始學生難理解課本中給出的概念，在教學中，教師不能停留于只讓學生關注對其表達式和取值范圍的討論，而應先選取具體事例，讓學生主動探討體會函數能夠反映客觀事物的變化規律。如可先讓學生指出下列問題中哪些是變量，它們之間的關系可以用什么方式表達：①汽車的速度是每小時50千米，在t小時內行駛的路程是s千米；②圓的面積s與圓的半徑r；③由某一天氣溫變化的曲線所提示的氣溫和時間。學生思考后還要讓他們反復比較，通過探究性學習得出各例中兩個變量的本質屬性：一個變量每取一個確定的值，另一個變量也相應地唯一確定一個值。然后讓學生自己舉出函數的實例，辨別真假例子，水到渠成地概括出函數定義。至此學生就能體會到函數“變”的屬性，至于變化規律如何?教師要繼續引導探究實際事例，從而達到對概念的鞏固。

二、在問題情境中進行探究性學習

學習應是一個再發現、再創造的過程，教師要引導學生置身于問題情境中，提示知識背景，讓學生體驗研究一個新問題的過程，展示思維過程，體驗探究的真諦。如在“三角形三邊關系”的教學中，教師可以先要求學生將事先準備好的長度為3cm、4cm、5cm、6cm、10cm、12cm的六根小木棒拿出來進行動手操作，任取三根將其首尾相接，拼成三角形。讓學生細致觀察后提出問題，教師把問題篩選后提供給學生，為他們創設問題情境，以便進一步探究學。

問題1：任意三根小棒能否拼成一個三角形?

問題2：有幾組三根小棒能拼成一個三角形?

問題3：有幾組三根小棒不能拼成一個三角形?

問題4：通過上述的動手操作，請猜想三角形中任意兩邊的長度之和(或差)與第三邊的長度之間存在什么關系?

問題5：試用簡潔的文字歸納你的猜想?又如何證明你的猜想?

這些問題形成一個思維鏈，學生既有興趣探究，又發展了思維，在探究中還可能培養創新精神。

三、在例題和習題的引伸拓展中進行探究性學習

教材中例題和習題都具有很高的數學價值。例題講解后，教師應對例題或習題進行多角度，多層次地改變題中的條件與結論并作適當的引伸，讓學生求解或用多種方法求解，通過這樣探究性學習，不僅加深學生對問題結構和特征的理解，而且有利手培養學生發散性的思維，提高他們分析問題和解決問題的能力。這樣，讓學生在探究中發現，在探究中創造就能實現了。

例如華師大版數學教材七年級下冊習題9.1第4小題：如圖1，在△ABC中，∠ABC=80°，∠ACB=50°,BP平分∠ABC，CP平分∠ACB，求∠BPC的度數。對于這個題目的求解，學生不難證明，但教學不能到此為止，應以原題的條件為基礎，引導學生進行多方面的探索。

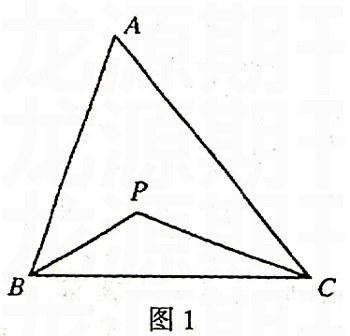
探索1：改變題目中的已知角的度數，如“∠ACB=50°”改為“∠ACB=60°”；

探索2：改變題目中的已知條件，如“∠ABC=80°，∠ACB=50°”改為“∠A=60°”或“∠A=70°”：

探索3：在探索2的研究下，條件改為“∠A=α”，用含x的代數式表示∠BPC。

這樣，學生在例題或習題的引伸拓展中進行探究性學習，思維活躍，能力逐漸形成。

四、在概括數量關系、變化規律中進行探究性學習

有效的數學學習過程不能單純地依賴模仿與記憶，教師引導學生主動地從事觀察、實驗、猜測、驗證、推理與交流等活動，從而使學生加深對數學知識的理解，形成有效的學習策略。在代數式、方程、函數、不等式教學中，擁有不少用來表達各種數學規律的模型的內容，教師在數學中要引導學生進行觀察、實驗、猜測、驗證、推理與交流等活動，尋找探索事物的數量關系和變化規律，從而提高數學能力。

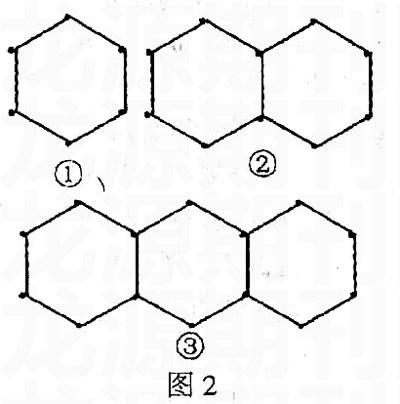
如：用火柴棒按圖2所示的方式擺圖形，按照這樣的規律繼續擺下去，第4個圖形需要____________根火柴棒，第n個圖形需要——根火柴棒(用含n的代數式表示)。

學生經過動手參與，可以得到搭一個六邊形需6根，搭兩個六邊形需11根，……讓學生感受在圖形的變化過程中火柴棒數的數量變化，然后引導學生探究n個三角形所需火柴棒數，充分肯定學生用不同的角度觀察、思考，得出相同結果。

思路1：每個六邊形要6根，n個需6n根，其中(n-1)個六邊形有一根共用，所以需要6n-(n-1)=5n+1根。

思路2：從第二個六邊形開始需要5根，共要5(n-1)根，加上第一個三角形的6根，共6+5(n-1)=5n+1根。

思路3：每個六邊形都要5根，n個要5n根，其中第一個多一根，故需要5n+1根。

學生在探究的過程中，經歷了一個從具體到抽象的數學化的過程，加深對數學的理解，在與他人交流的過程中，逐漸完善自己的想法。

五、注重在初中性內容中進行探究性學習

教師應盡可能多地提供一些現實生活中學生感興趣的事例進行探究，如市場銷售問題、股票風險投資、

_貸款利息計算、道路交通狀況、環境資源調查、有獎銷售討論、體育比賽研究等。通過對實踐性內容的探究學習，學生的實踐能力大大提高了。

測量建筑物或樹的高度，是一個典型的實踐性探究內容。學習了“解直角三角形”后，教師應注重相關的實踐性內容，可以提出這樣的問題：怎樣測量學校旗桿的高度?針對各種不同的實際情況，設計不同的測量方法。教師組織學生到實地考察，記錄所看到的實際情形，每人設計測量的具體方案，然后分四人小組討論交流，把本小組的各種設想進行匯總和整理，再選擇幾種典形的方案在全班介紹。這樣學生積極性很高，又體驗到解決問題策略的多樣性。又如學校建新校舍，要在長100米，寬80米的矩形空地上建造一個花園，要求綠化面積是空地面積的一半，請為學校展示你的設計方案。這些例子很多，不同水平的學生都可以參與探索，在探究學習中，充分發揮學生的想象力，展示學生的思維方式，真正做到自主探索，提高創新精神和實踐能力。

總之，在初中數學教學中開展探究性學習，培養學生探究學習的習慣和能力，是新世紀數學改革的一個重大舉措，是時代發展的需要，是我們數學教師必須實施的課題。學生探究性學習活動能否順利實施，關鍵在于教師能否創造適宜的教學情境和進行合理的引導，在新課程實施過程中，教師要運用一切可能的手段，不斷優化教學設計，創設有效的探究時間和空間，營造良好的探究氛圍，激發學生的學習興趣，讓每個學生都有主動探究的機會，從而真正實現“不同的人在數學上得到不同的發展”的新理念。