以《幾何畫板》為載體,開展數學實驗教學
數學實驗教學是指根據教學目標,充分利用實驗手段尤其是運用現代教育技術,創設問題情境,引導學生參與實踐、自主探索、合作交流,從而發現問題、提出猜想進而驗證猜想和創造性解決問題的一種教學。數學實驗是保證學生主體參與的重要途徑,它能揭示數學知識的發生和發展過程。
改變了學生的學習
1.學生由“聽數學”變為“做數學”。通過做數學實驗,學生的地位從被動接受轉為主動參與。
【案例】勾股定理
(1)教師用《幾何畫板》畫出直角三角形,借軟件自帶的測量功能,測出斜邊的長。并適時啟迪、誘導學生思考直角三角形三邊的關系。
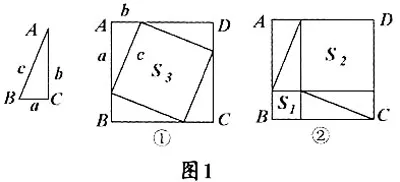
(2)根據圖形面積的性質,運用“面積分割、移補,拼湊”的實驗操作,讓學生“拖動”鼠標把四個直角邊長為a和b、斜邊長為c的全等直角三角形放到邊長為a+b的正方形ABCD中。學生發現有以下兩種放法(如圖1),并從理論上得出了a2+b2=c2的結論。
2.學生由“看演示”變為“動手操作”。數學實驗使單一的媒體呈現轉變為學生的認知工具。通過即時功能和動畫功能有效地揭示數學思維的過程和實質。學生通過動手操作,去探索發現、猜測和驗證,成為實踐的主體。
【案例】勾股定理(如圖2)
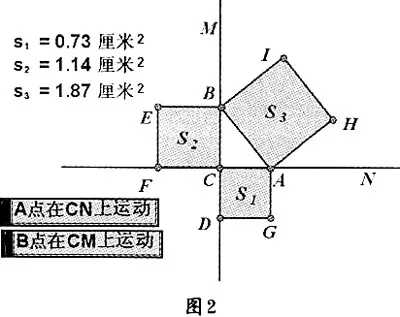
(1)分別以直角三角形ABC的三邊長為邊長作三個正方形,利用《幾何畫板》自帶的“面積”功能測算以AB為邊長的正方形的面積S3,以及以BC和AC為邊長的正方形的面積S2和S1。
(2)通過點擊“A點在CN上運動”、“B點在CM上運動”動畫(三個正方形的大小在不斷地變化),讓學生經過觀察動態圖形和數據變化,發現其中不變的數量關系:S1+S2=S3,即AC2+BC2=AB2(勾股定理),從而想到用面積的方法來說明直角三角形的三邊關系。
3.學生由“機械學習”變為“主動探索”。數學實驗的教學使以講授說明為主的單一化教學過程轉變為通過情境創設、問題探索、協作學習、意義建構等以學生為主體的教學過程。
【案例】正弦和余弦(如圖3)
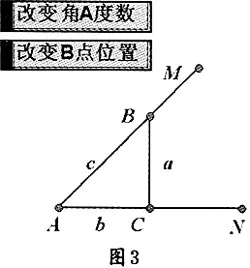
(1)在直角三角形BAC中,保持∠A不變,拖動點B在AM上運動,發現—、—的值始終保持不變。
(2)當∠A變化時,由測量功能可知:—隨∠A的增大而增大,—隨∠A的增大而減小,學生在操作中發現0<—<1、0<—<1,并試圖建立一種表示形式來反映隨著∠A的變化,—和—有一個怎樣的與之相對應的關系,從而自然地引出正弦和余弦的概念。
給了學生發現問題的機會
【案例】三角形的中位線
(1)教師給出一個漂亮的荷花池塘后提問:如何測量它的寬?
(2)提供一個測量的方法:用電腦把池塘抽象化(如圖4)后只需測量BC的長度。即,在池塘一側的平地上選一點A,再分別找出線段AB、AC的中點D、E,測得DE=18米,從而求得池塘寬BC=36米。
9h7V+BVhQljJcaTrTGGiew== (3)據此問學生:此人的方法有道理嗎?究竟有什么奧妙呢?
(4)通過《幾何畫板》度量三邊長度及DE長度,并將結果顯示在屏幕上。請學生拖動三角形的任意一個頂點,通過觀察回答下列問題,讓學生自己探索、實驗:①中位線DE與三角形各邊有怎樣的位置關系?②中位線DE與三角形各邊的長度有怎樣的相等關系?③猜想:三角形的中位線有什么性質?④你能證明這一猜想嗎?
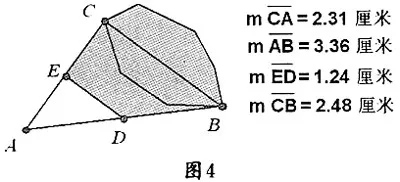
隨著學生拖動三角形的任意一個頂點,中位線的位置相應地動態改變,且三角形三條邊以及中位線的長度也隨之改變。從而充分體現了三角形的任意性,并引導學生關注變化過程中的不變關系、不變量,讓學生通過觀察發現規律。
促進學生對知識的理解和記憶
【案例】二次函數y=ax2+bx+c的圖像
(1)教師用《幾何畫板》畫好二次函數y=ax2+bx+c的圖像(如圖5),然后拖動鼠標,分別調整a、b、c 的大小,觀察圖像的變化,根據不同的變

