長方體上均勻分布的密度函數
陳光曙
(江蘇財經職業技術學院,江蘇淮安 223003)
長方體上均勻分布的密度函數
陳光曙
(江蘇財經職業技術學院,江蘇淮安 223003)
討論了長方體上均勻分布密度函數問題,得到了長方體體積的估計量、估計量的點估計及估計量的密度函數.
估計量;均勻分布;密度函數;長方體
1 引言
均勻分布上概率統計中的重要分布,具有廣泛的應用價值.由于隨機取的點集被廣泛應用于許多概率模型中,如:流行病學、遺傳學及交通理論等.因此,均勻分布及其相關統計量的研究也引起了眾多學者的關注.如X~U(a,b)(a<b,a,b均為未知參數),設X1,X2,···,Xn是X的簡單隨機樣本,關于參數a,b的估計量,人們更為關注的是它們的極大似然估計量文[1-2]曾研究過參數a,b的估計量的有關性質,并給出許多重要結論,給出了實數a,b的區間估計.文[3-4]進一步研究了一維均勻分布U(a,b)的區間長度L=b?a的估計問題.文[5]在文[3]的基礎上,研究了矩形區域上均勻分布的面積估計問題.本文在文[1-5]的基礎上,著重研究空間長方體G上服從均勻分布的體積V的估計量?V的概率密度函數以及V的點估計問題.
2 有關記號及引理
為敘述方便,引入以下記號和引理:
設G為空間的長方體,G={(x,y,z)|a<x<b,c<y<d,e<z<f},其中a,b,c,d,e,f均為未知參數,V=(b?a)·(d?c)·(f?e)表示G的體積.
設(X,Y,Z)在G上服從均勻分布,記為(X,Y,Z)~U(G),其聯合密度為


3 體積V的統計量及其密度函數


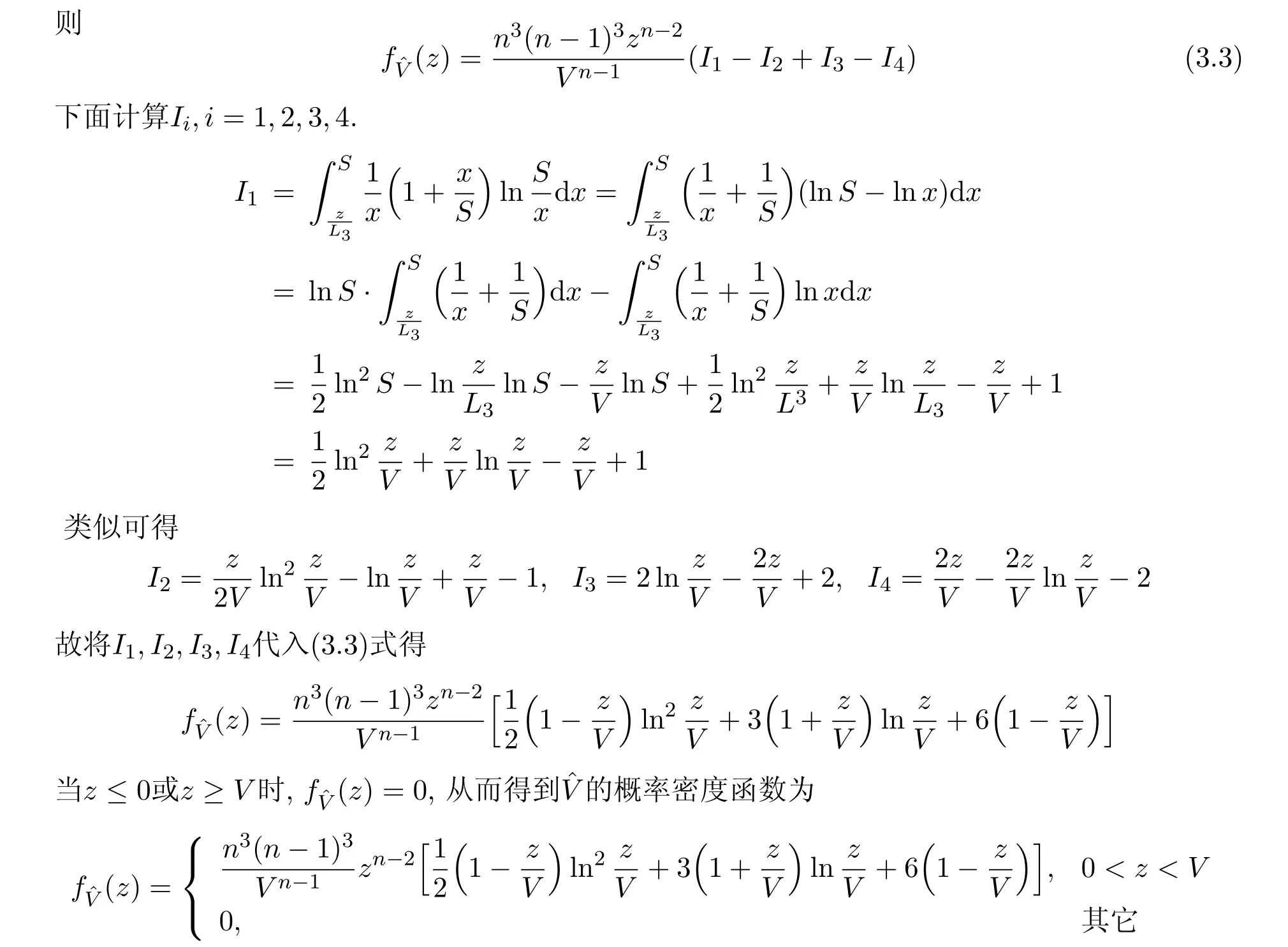
關于體積V的密度函數的性質以及V的區間估計問題,我們將另文討論.
[1]潘高田,胡軍峰.小樣本的均勻分布參數的區間估計和假設檢驗[J].數學的實踐與認識,2002,32(4):629-631.
[2]顏貴興.均勻分布參數的矩估計與最大似然估計[J].廣西師院學報:自然科學版,2001,18(2):76-79.
[3]陳光曙.均勻分布區間長度的估計[J].大學數學,2005,21(4):120-124.
[4]陳光曙.均勻分布區間長度估計量的漸近分布及其性質[J].山東師范大學學報,2005,20(3):8-10.
[5]劉兆君.二維均勻分布矩形區域面積的估計[J].大學數學,2007,23(4):155-159.
Density function of uniform distribution on the cuboid
CHEN Guang-shu
(Jiangsu Vocational and Technical College of Finance and Economics,Huaian223003,China)
In this paper,the problem of density function which is in the uniform distribution on the cuboids is discussed.From that,the volume estimator,as well as its point estimate and density function on the cuboids have been given.
estimation,uniform distribution,density function,cuboid
O211.1
A
1008-5513(2009)04-0721-04
2008-02-10.
江蘇省高校自然科學基金(05KJD110034).
陳光曙(1961-),教授,研究方向:概率論與數理統計.
2000MSC:60D05

