一種新廣義凸多目標分式規劃的最優性充分條件
李動鋒,邱根勝
(南昌航空大學應用數學系,江西南昌 330063)
一種新廣義凸多目標分式規劃的最優性充分條件
李動鋒,邱根勝
(南昌航空大學應用數學系,江西南昌 330063)
提出了(F,α,ρ,θ)-b-凸函數的概念,它是一類新的廣義凸函數,并給出了這類廣義凸函數的性質.在此基礎上,討論了目標函數和約束函數均為(F,α,ρ,θ)-b-凸函數的多目標分式規劃,利用廣義K-T條件,得到了這類多目標規劃有效解和弱有效解的幾個充分條件,推廣了已有文獻的相關結果.
多目標分式規劃;廣義凸函數;最優性條件
眾所周知,凸性概念在優化理論中起著關鍵性的作用,因此各種凸性概念的拓廣以及相應廣義凸性下目標規劃解的最優性條件的研究受到了廣泛關注.2001年,Liang[1]提出(F,α,ρ,d)-凸函數的概念,并就單目標分式規劃問題給出了一些最優性充分條件.本文在文[1]的基礎上,給出一類新的廣義凸函數-(F,α,ρ,θ)-b-凸函數,并在此假設下討論了多目標分式規劃的最優性充分條件.
本文考慮如下的多目標分式規劃問題
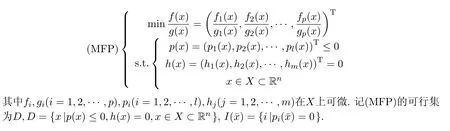
1 定義與引理
定義1.1給定一個非空開集X?Rn,函數F:X×X×Rn→R稱為次線性的,如果對任意的x1,x2∈X
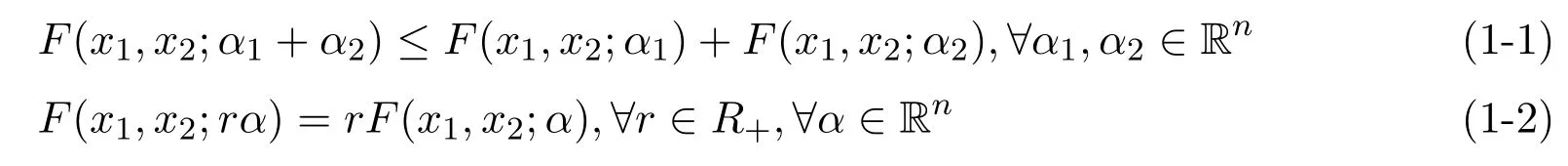
顯然,對于次線性函數F,由(1-2)式可得F(x1,x2;0)=F(x1,x2;0α)=0F(x1,x2;α)=0.
定義1.2設X?Rn,X為非空開集,函數F:X×X×Rn→R為次線性的,f:X→R在ˉx處可微,α:X×X→R++,b:X×X→R+,θ:X×X→Rn,ρ∈R


2 最優性條件






[1]Liang Z A,Huang H X,Pardalos P M.Optimality conditions and duality for a nolinear fractional programming problems[J].Opti.Theo.Appl.,2001,110:611-619.
[2]Liang Z A,Huang H X,Pardalos P M.Efficiency conditions and duality for a class of multiobjective fractional programming problems[J].Global Optim.,2003,27:447-471.
[3]林銼云,董加禮.多目標優化的方法與理論[M].遼寧:吉林教育出版社,1992.
[4]邱根勝.廣義凸多目標分式規劃解的充分條件及其對偶定理[J].南昌航空工業學院學報,2001,15(1):68-73.
[5]劉三明,馮恩民.具有凸的分式規劃問題的最優性條件和對偶性[J].數學的實踐與認識,2005,35(12):174-182.
[6]馮芙葉,賈繼紅,聶成.一類非光滑規劃問題的最優性和對偶[J].純粹數學與應用數學,2005,3:246-249.
Optimality conditions for multi-objective fractional programming with a new formulation of generalized convexity
LI Dong-feng,QIU Gen-sheng
(Department of Applied Mathematics,Nanchang Hangkong University,Nanchang330063,China)
In this paper,we present a new formulation of generalized convex function(F,α,ρ,θ)-b-convex function,obtain some properties;and a class of the multi-objective fractional programming is studied,where the involved functions are(F,α,ρ,θ)-b-convex function,using the generalized K-T condition,some sufficient conditions for a efficient solution and a weak efficient solution for the multi-objective fractional programming are obtained,and these results generalize some current results.
multi-objective fractional programming,generalized convex function,optimality condition
O221.6
A
1008-5513(2009)04-0807-09
2007-09-18.
李動鋒(1980-),碩士,研究方向:最優化理論與算法.
2000MSC:49K99

