一類分類數據列聯表中基于檢驗功效的樣本量研究

王順芳,王學仁

(1.云南大學信息學院,云南昆明 650091;2.云南大學統計系,云南昆明 650091)

一類分類數據列聯表中基于檢驗功效的樣本量研究

王順芳1,王學仁2

(1.云南大學信息學院,云南昆明 650091;2.云南大學統計系,云南昆明 650091)

對不完全2×2列聯表中關于風險比(RR)的假設檢驗問題,使用基于約束性極大似然估計下的Wald檢驗統計量和對數變換檢驗統計量,導出了滿足預先給定功效的樣本量公式.模擬結果驗證了所給檢驗和樣本量公式的合理性,實例分析解釋了上述方法的應用.

約束性極大似然估計;功效;樣本量

1 引言

在流行病學、生物學以及各種臨床研究中經常需處理大量的分類數據問題,其中一類較常見的分類數據可概括為不完全2×2列聯表的形式,這類列聯表中某一格(一般位于非對角元素上)的頻數始終為零,這是結構本身所固有的,稱為”結構零”.一般情況下,此類列聯表的結構可概括為表1.表1中的結構零位于第(2,1)格,其中0＜πij＜1((i,j)=(1,1),(1,2)和(2,2))代表相應

表1 不完全2×2列聯表

事件發生的概率,π1+=π11+π12,π1++π22=1.a,b,d是相應事件發生的頻數,a+b+d=n. 當n一定時,(a,b,d)服從三項分布,其概率分布記為

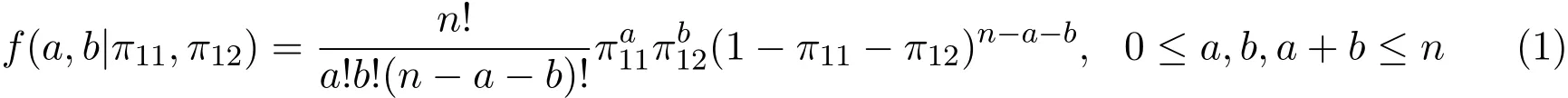
研究不完全2×2列聯表時,生物醫學上一個常用的統計量是風險比(Risk Ratio,簡記為RR),其定義為RR=(π11/π1+)/π1+=π11/.

關于不完全2×2列聯表中的風險比(RR),已有的研究工作如下:文[1]討論了大樣本下RR的置信區間估計問題,其中分別使用了基于樣本估計的Wald統計量、基于樣本估計的對數變換統計量以及基于Fieller定理的統計量;文[2]使用Wald統計量和對數變換統計量從小樣本的角度研究了RR的精確非條件推斷,提出了檢驗RR等于某一固定值?0的精確非條件檢驗和近似非條件檢驗;文[3]提出了檢驗風險比的Score統計量,研究了基于Score方法的置信區間并和文[1]討論過統計量進行比較.以上文獻中,總的來說是Score方法的統計性能較好,在Score方法中,比較重要的一點就是對參數的約束性極大似然估計,文[4]的討論也表明了在其所研究的情況下基于約束性極大似然估計優于基于樣本的估計,于是文[5]使用了基于約束性極大似然估計的Wald統計量和對數變換統計量,對不完全2×2列聯表中的風險比進行置信區間構造,導出在一定置信水平下控制置信區間寬度的樣本量公式.本文繼續使用基于約束性極大似然估計的Wald統計量和對數變換統計量,研究RR的大樣本假設檢驗問題,給出了基于檢驗功效的漸近樣本量公式.

2 兩種基于約束性極大似然估計的漸進檢驗

它漸近服從標準正態分布;給定顯著性水平α,當|T1|≥zα/2時,可拒絕原假設H0,這里zα/2表示標準正態分布的上α/2分位點.

漸近服從標準正態分布.

3 功效和樣本量計算

定理1若使用檢驗統計量T1對假設(2)進行檢驗,在給定的顯著性水平α下,為達到功效1?β所需的近似樣本量為

定理2若使用檢驗統計量T2對假設(2)進行檢驗,在給定的顯著性水平α下,為達到功效1?β所需的近似樣本量為

可得檢驗的漸近樣本量公式為(6)式.

4 模擬研究

在很多實際問題中,由于似然函數和極大似然估計的復雜性,統計上常需一些研究技巧(例如文[8]).本節為評價兩種基于約束性極大似然估計的漸近檢驗的樣本量公式(5)和(6)的精確性(即控制功效的準確程度),擬在各種參數設置下進行模擬計算.

首先應用公式(5)和(6)計算了顯著性水平為5%、功效為80%(即β=0.2)下的漸近樣本量.為評價這些近似樣本量對功效控制的精確程度,本節類似于文[6]的模擬方法,使用如下公式計算了和這些樣本量對應的經驗功效和經驗第一類錯誤率

其中M是試驗重復次數,(a,b)(i)是第i次試驗的觀察值,R={(a,b)(i):|Tj|≥zα/2,j= 1或2}是拒絕域,I(·)是示性函數(當(a,b)(i)∈R時其取值為1,否則其取值為0);且當各(a,b)(i)(i =1,…,M)是在H0下產生的隨機觀察值時,(7)式表示經驗第一類錯誤率,當各(a,b)(i)(i= 1,…,M)是在H1下產生的隨機觀察值時,(7)式表示經驗功效.模擬研究中,試驗重復次數根據收斂情況設置為10000(即M=10000),當某次試驗產生的觀察值(a,b)使得統計量T1或T2沒有定義時,就用a+0.5,b+0.5,n+1.5分別替換a,b,n后再做計算.整個結果歸納為表2.

表2 統計假設(2)在控制檢驗功效為80%下的近似樣本量(α=5%),及相應的經驗功效(EP)和經驗第一類錯誤率(ETI)

表2 (續)

分析表2,總的來說,檢驗T1和T2得到的樣本量比較接近,其經驗功效一般都能保證80%的水平,經驗第一類錯誤率也都非常接近5%,說明樣本量公式(5)和(6)都比較精確.進一步比較發現,當?＜?0時,同樣的參數設置下,檢驗T1得到的樣本量比T2的大;而當?＞?0時,檢驗T1得到的樣本量比T2的小.因此在實際應用中,當?＜?0時,可使用基于約束性極大似然估計的對數變換檢驗統計量;當?＞?0時,可使用基于約束性極大似然估計的Wald檢驗統計量.

5 實例分析

本節將前面所得方法和結論應用于文[7]中提到的一實例:小牛的二次感染數據.這一實例考慮了出生于佛羅里達州奧基喬比的156頭小牛組成的一個樣本,先根據它們在出生60天后是否感染了肺炎分成兩類,并對感染了肺炎的小牛進行治療,等到初次感染治愈后再過兩周又根據它們是否感染肺炎再分類,從理論上來說,小牛若沒有初次感染,就不存在二次感染,這樣在2×2列聯表中就引入了一個“結構零”,它對應于初次無感染而二次被感染的情況.此例的數據結構見表3.根據表3的數據,風險比(RR)的樣本估計為??=0.5411.考慮假設問題(2),取?0=1.0,經計算,T1=?3.2563,T2=?4.3579,它們相應的p值分別為0.0011和0.00001,若顯著性水平為0.05,則可拒絕H0,說明初次感染和二次感染的概率不等.

對這個問題作進一步的拓展,假定研究者想做一個類似于文[7]工作的另一種流行病學研究,同樣考慮檢驗假設(2),其中?0=1.0,顯著性水平給定為α=0.05.當備擇假設成立時,例如?=0.9,π1+=0.7,一個感興趣的問題是需要多大的樣本量才能達到80%的功效.通過計算就可以得到,對應于統計量T1,T2分別需要911和873個個體.

表3 小牛二次感染問題的統計數據

[1]Lui K J.Interval estimation of risk ratio between the secondary infection given the primary infection and the primary infection[J].Biometrics,1998,54(2):706-711.

[2]Tang N S,Tang M L.Exact unconditional inference for risk ratio in a correlated 2×2 table with structural zero[J].Biometrics,2002,58(4):972-980.

[3]Tang M L,Tang N S,Carey V J.Confidence interval for rate ratio in a 2×2 tables with structural zero:an application in assessing false-negative rate ratio when combining two diagnostic tests[J].Biometrics,2004,60(2): 550-555.

[4]Wang S F,Tang N S,Wang X R.Analysis of risk difference of marginal and conditional probabilities in an incomplete correlated 2×2 table[J].Computational statistics and data analysis,2006,50(6):1597-1614.

[5]王順芳,王學仁.不完全2×2列聯表中基于置信區間的樣本量研究[J].云南大學學報:自然科學版,2007,29(2):109-113.

[6]Wang S F,Wang X R.Homogeneity test of risk differences of marginal and conditional probabilities in several incomplete correlated 2×2 tables[J].Communications in Statistics-Theory and Methods,2007,36(16),2877-2890.

[7]Agresti A.Categorical Data Analysis[M].New York:Wiley,1990.

[8]任麗梅,師義民.多重II型刪失數據場合Logistic分布參數的近似似然函數[J].純粹數學與應用數學,2007,23(3):341-346.

Sample size determination for power in a sort of contingency table

WANG Shun-fang1,WANG Xue-ren2
(1.School of Information Science and Engineering,Yunnan University,Kunming650091,China; 2.Department of Statistics,Yunnan University,Kunming650091,China)

To test the hypothesis about risk ratio(RR)in an incomplete correlated 2×2 table,a Wald-type test statistic and a logarithmic transformation test statistic on the basis of the constrained maximum likelihood estimation(CMLE)method are proposed.Sample size formulae are derived to guarantee a prespecified power. Simulation results show that the above tests and formulae are valid.An example is used to illustrate the method.

constrained maximum likelihood estimation,power,sample size

O212.1

A

1008-5513(2009)03-0425-06

2008-03-12.

國家自然科學基金(10901135,10626048,10761011),云南省社發計劃應用基礎研究面上項目(2008CD081),云南大學中青年骨干教師培養計劃專項經費.

王順芳(1974-),副教授,博士,研究方向：數理統計.

2000MSC:62F03,62P10