多點收縮混沌優化方法及全局收斂性證明

劉勇,陸軍,徐裕生,李陽

(1.西安建筑科技大學理學院,陜西西安 710055;2.鄭州師范高等專科學校,河南鄭州 450044)

多點收縮混沌優化方法及全局收斂性證明

劉勇1,陸軍2,徐裕生1,李陽1

(1.西安建筑科技大學理學院,陜西西安 710055;2.鄭州師范高等專科學校,河南鄭州 450044)

針對目前混沌優化算法在選取局部搜索空間時的盲目性,提出一種具有自適應調節局部搜索空間能力的多點收縮混沌優化方法.該方法在當前搜索空間搜索時保留多個較好搜索點,之后利用這些點來確定之后的局部搜索空間,以達到對不同的函數和當前搜索空間內已進行搜索次數的自適應效果.給出了該算法以概率1收斂的證明.仿真結果表明該算法有效的提高了混沌優化算法的性能,改善了混沌算法的實用性.

混沌優化;多點收縮混沌優化算法;全局收斂性;概率1收斂

1 引言

混沌是一種普遍的非線性現象,具有隨機性、遍歷性和內在的規律性的特點.基于混沌遍歷性的混沌優化一經出現,其直觀、易實現的特點就引起了廣泛關注[13].但目前混沌優化發展歷史較短,因此許多問題還有待進一步研究和討論.現有的研究表明,當直接利用混沌變量進行搜索時:1)單純的提高迭代步數不能顯著的提高算法搜索的遍歷程度;2)多軌道并行搜索不能顯著提高混沌搜索的遍歷程度;3)在粗略搜索的最優點附近進行細搜索,可能導致當前最優點偏離全局最優點[4],影響算法的搜索速度.由此可見,在大范圍的搜索后對有較大概率出現全局最優點的局部空間進行再搜索是提高混沌優化算法性能的一種較為理想的改進方法.但易知不同的函數在進行局部搜索前需要進行的搜索次數是不同的,需要進行局部搜索的區域也是不同的,故對局部搜索的控制策略和局部搜索策略的選取是至關重要的.而以往的混沌算法都是在進行一定次數的混沌搜索的基礎上,以固定的比例縮小搜索空間[23],顯然這種局部搜索空間的選取是較為盲目的.本文提出利用多個較好搜索點來確定局部搜索空間的策略,這種策略能針對不同的函數和針對在當前搜索空間內已進行搜索的次數自適應的調節之后的局部搜索空間.通過這種改進,既保證了算法的收斂速度又可對算法的全局收斂效果進行控制,從而大大提高了混沌算法的實用性.

2 算法的初步介紹

2.1 局部搜索空間的選取策略

多點收縮混沌優化方法局部搜索空間選取策略如圖1所示.其中A為當前搜索空間, “·”表示在空間A內已得到的所有搜索點,“*”表示在空間A內通過比較得出的前個較好搜索點.本文選取包含所有“*”在內的最小超長方體B為相對空間A的局部搜索空間,同樣在B空間上可繼續按上述過程再進行搜索并重新確定相對B空間的局部搜索空間,直到達到算法終止條件.

圖1 局部搜索空間選取策略示意圖

2.2 算法自適應控制能力的分析

對于性態較好的函數和在空間A內搜索點數iter相對較多時,搜索空間宜快速收縮以提高搜索效率;而在相反情況時,搜索空間則不宜縮小過快以避免搜索陷入局部最優.當按照上述方法確定局部搜索空間時,由于混沌變量具有隨機性、遍歷性的特點,故函數性態的好壞和iter的大小將直接決定搜索得到的num個較好點的集中和分散程度,從而決定了之后局部搜索空間的大小,而多個較好點的使用又可以極大概率的保證全局最優點落在由其決定的局部搜索空間之中,由此就實現了算法對上述不同情況的自適應控制.

3 多點收縮混沌優化算法

對于連續的全局優化模型

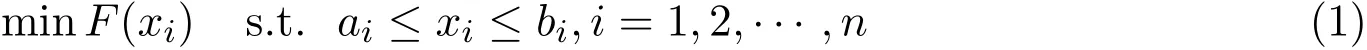
4 算法全局收斂性的證明

4.1預備知識

4.2 全局收斂性證明

5 數值方真

5.1 算法對隨機參數自適應性測試

為了檢驗算法對不同函數和參數的自適應性.我們選取了兩個經常被用來測試混沌化算法有效性的兩個函數進行了仿真測試.

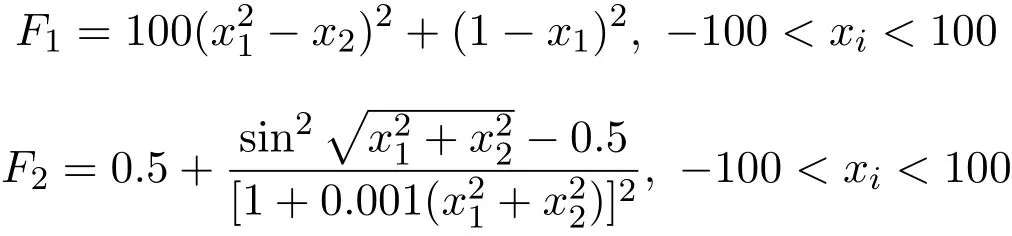
設計隨機操作如下:

1)混沌變量在區間(0,1)上隨機取定;

2)參數iter在100～1000之間隨機取定;

3)參數num在10～20之間隨機取定.

F1和F2理論最小值皆為0.表1為在以上的隨機操作和ε=0.01的規定下我在P4(1.4G) 的PC機上連續對F1和F2進行了10次運算的結果.

圖1 算法隨機參數仿真結果

由表1可見對F1和F2的10次隨機仿真運算均能很好的收斂到各自的理論值,并且所耗費的時間基本是相同的,而當進行隨機參數實驗時文[1-3]的算法均很難在短時間內收斂,這充分證明了本文算法的有效性和對不同的參數和函數的自適應性.

5.2 算法對于不同維數的自適應性

一個好的優化算法最終是為解決實際問題服務的,而實際問題一般為高維函數,為了測試本算法對高維函數的適應性,我們進行如下數值仿真.

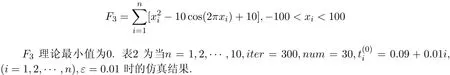
由表可見當n=1,2,…,10時算法均能全局收斂,雖然隨著函數維數的增長計算精度有所降低,且計算時間快速增長,但是由于所有計算結果都是在相同參數下計算得出的,所以整體的計算結果還是十分令人滿意的.

6 結語

本文提出的多點收縮混沌優化算法,對混沌算法應如何縮小搜索空間,如何設計算法終止條件,如何選取初始控制參數和控制策略給出了一種較為理想的解決方案.由證明過程可見只要每次保留的較好搜索點數num足夠大,本算法可以以概率1收斂于全局最優解.而在實際應用中可以通過控制num的取值,快速的得出滿足實際需求的最優解.

圖2 算法對不同維函數仿真結果

[1]李兵,蔣慰孫.混沌優化方法及其應用[J].控制理論與應用,1997,14(4):613-615.

[2]張彤,王宏偉,王子才.變尺度混沌優化方法及其應用[J].控制與決策,1999,14(3):285-288.

[3]修春波,劉向東,張寧河.雙混沌機制優化方法及其應用[J].控制與決策,2003,18(6):724-726.

[4]杜守強,陳元媛.推廣線搜索下一類共軛梯度法的全局收斂性[J].純粹數學與應用數學,2004,20(3):209-212

[5]李宏,王宇平,焦永昌.解非線性兩層規劃問題的新的遺傳算法及全局收斂性[J].系統工程理論與實踐,2005, 26(3):62-71

Multipoint shrinking chaos optimization algorithm and its global convergence

LIU Yong1,LU Jun2,XU Yu-sheng1,LI Yang1
(1.School of Science,Xi’an University of Architecture and Technology,Xi’an710055,China; 2.Department of Mathematics,Zhengzhou Teachers College,Zhengzhou450044,China)

A multipoint shrinking chaos optimization algorithm which local searching space can be decided under an self-adaptive contral strategy is proposed.The method keeps multiple better searching points at present searching space to decide its local searching space later.By this way the method have a self-adaptive on different functions and different times the search has carried out before.The global convergence of the algorithm are proved.Simulation results show that the algorithm can improve the chaos optimization algorithm’s performance effectivly as well as make the chaos optimization more practical.

chaos optimization,multipoint shrinking chaos optimization algorithm,global optimization,almost sure convergence

O221

A

1008-5513(2009)03-0491-06

2007-11-28.

國家自然科學基金(70173037).

劉勇(1979-),碩士,研究方向：最優化理論.

2000MSC:40K