“平面圖形的面積”編寫特點(diǎn)與教學(xué)建議
黃偉星
一、教學(xué)內(nèi)容的編排
平面圖形的面積屬于圖形與幾何領(lǐng)域中的測(cè)量部分,根據(jù)《全日制義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(修改稿)》(簡(jiǎn)稱《標(biāo)準(zhǔn)》)內(nèi)容標(biāo)準(zhǔn)中的要求,蘇教版教材分3次進(jìn)行編排。

二、教材編排的特點(diǎn)
1、選擇現(xiàn)實(shí)素材。
從上面表中整理的教學(xué)內(nèi)容可以看出:蘇教版教材“平面圖形的面積”的編寫以《標(biāo)準(zhǔn)》中“測(cè)量”部分的內(nèi)容標(biāo)準(zhǔn)為依據(jù),全面落實(shí)《標(biāo)準(zhǔn)》提出的理念和目標(biāo)。教材中學(xué)習(xí)素材的選擇,與所教學(xué)的數(shù)學(xué)內(nèi)容有本質(zhì)聯(lián)系,有利于學(xué)生對(duì)數(shù)學(xué)實(shí)質(zhì)的理解。如“面積的意義”選用的素材符合學(xué)生的生活現(xiàn)實(shí)和數(shù)學(xué)現(xiàn)實(shí),幫助他們經(jīng)歷從現(xiàn)實(shí)情境中抽象出數(shù)學(xué)知識(shí)和方法的過(guò)程。教材從感知物體表面的大小——比較平面圖形面積的大小——體驗(yàn)周長(zhǎng)與面積的區(qū)別三個(gè)層面進(jìn)行編排,循序漸進(jìn),逐步深入,幫助學(xué)生準(zhǔn)確理解面積的含義。與老教材相比,新教材沒(méi)有給出面積的定義,而是充分借助實(shí)例,從物體表面到平面圖形,從直觀到抽象,讓學(xué)生通過(guò)大量豐富的例子認(rèn)識(shí)面積。
2、展開探索過(guò)程。
根據(jù)“測(cè)量”部分教學(xué)內(nèi)容的特點(diǎn),教材設(shè)計(jì)了必要的數(shù)學(xué)活動(dòng),遵循操作——發(fā)現(xiàn)——?dú)w納——應(yīng)用的原則,讓學(xué)生通過(guò)觀察、實(shí)驗(yàn)、猜想、推理、交流、反思等,探索“平面圖形面積的計(jì)算公式”。如編排長(zhǎng)方形和正方形的面積計(jì)算時(shí),從拼長(zhǎng)方形、量長(zhǎng)方形,感受長(zhǎng)、寬與面積的聯(lián)系,到推想、討論長(zhǎng)方形面積的計(jì)算方法,以歸納的方式進(jìn)行學(xué)習(xí),在發(fā)現(xiàn)長(zhǎng)方形面積計(jì)算公式的基礎(chǔ)上演繹出正方形面積的計(jì)算公式。在編排多邊形面積的計(jì)算時(shí),充分借助學(xué)生的數(shù)學(xué)經(jīng)驗(yàn),將幾個(gè)平行四邊形轉(zhuǎn)化成長(zhǎng)方形,用分類研究的方法將兩個(gè)完全一樣的三角形拼成平行四邊形。在此基礎(chǔ)上,通過(guò)討論教材上設(shè)計(jì)的3個(gè)問(wèn)題,推導(dǎo)出多邊形面積的計(jì)算公式,培養(yǎng)學(xué)生的分析、推理和概括能力。
3、滲透數(shù)學(xué)思想。
數(shù)學(xué)中有一些重要的內(nèi)容、方法、思想是需要學(xué)生經(jīng)歷較長(zhǎng)的認(rèn)識(shí)過(guò)程,逐步理解和掌握的,如轉(zhuǎn)化、模型思想等。根據(jù)學(xué)生的年齡特征與知識(shí)積累,根據(jù)這部分教學(xué)內(nèi)容的特征,教材采用逐級(jí)遞進(jìn)、螺旋上升的原則滲透猜想、實(shí)驗(yàn)、轉(zhuǎn)化、歸納等重要的數(shù)學(xué)思想方法。如編排長(zhǎng)方形和正方形的面積計(jì)算時(shí),滲透了操作、歸納的思想,編排多邊形的面積計(jì)算時(shí),滲透了轉(zhuǎn)化、歸納的思想,編排圓的面積計(jì)算時(shí),從猜想——探索——推理,在將圓轉(zhuǎn)化成長(zhǎng)方形的過(guò)程中,進(jìn)一步感受轉(zhuǎn)化的思想。在解決問(wèn)題的策略教學(xué)中,教材編寫了轉(zhuǎn)化策略的學(xué)習(xí),通過(guò)回顧平面圖形面積的計(jì)算方法,使學(xué)生體驗(yàn)在推導(dǎo)平面圖形面積計(jì)算的方法時(shí),要化新為舊,化未知為已知。
4、形成系統(tǒng)結(jié)構(gòu)。
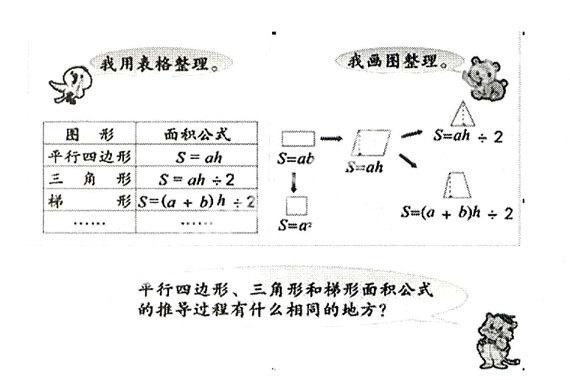
平面圖形的面積屬于“測(cè)量”部分的內(nèi)容,知識(shí)之間存在著非常本質(zhì)的內(nèi)在聯(lián)系。幫助學(xué)生理解類似的實(shí)質(zhì)性聯(lián)系,是數(shù)學(xué)教學(xué)的重要任務(wù)。教材在編寫這部分內(nèi)容時(shí),能緊扣知識(shí)之間的邏輯順序,以思想方法為主線。引導(dǎo)學(xué)生感悟這種順序,形成系統(tǒng)結(jié)構(gòu)。如多邊形面積的計(jì)算回顧與整理部分:
通過(guò)整理并比較面積公式推導(dǎo)過(guò)程中的相同點(diǎn),認(rèn)識(shí)到長(zhǎng)方形的面積計(jì)算公式是根本,以此為基礎(chǔ)構(gòu)建平面圖形面積公式之間的框架體系。
三、教學(xué)建議的思考
“圖形與幾何”內(nèi)容領(lǐng)域的核心之一是空間觀念,在教學(xué)中,教師要根據(jù)平面圖形的面積這部分知識(shí)的教學(xué)特點(diǎn),發(fā)展學(xué)生的空間觀念。
1、在認(rèn)識(shí)中理解數(shù)學(xué)概念。
平面圖形的面積教學(xué)從認(rèn)識(shí)面積過(guò)渡到測(cè)量并計(jì)算面積,在教學(xué)時(shí),應(yīng)十分重視引導(dǎo)學(xué)生建立面積、面積單位的表象。在建立表象的基礎(chǔ)上進(jìn)行估測(cè),增強(qiáng)學(xué)生對(duì)空間形式的直覺(jué)把握能力。如教學(xué)面積概念時(shí),教師要充分利用學(xué)生已有的知識(shí)和生活經(jīng)驗(yàn),讓學(xué)生通過(guò)摸、看、比、說(shuō)等活動(dòng),先認(rèn)識(shí)物體表面的大小,揭示面積的初步含義,并讓學(xué)生學(xué)會(huì)用“面積”這個(gè)詞去比較、描述和舉例。在此基礎(chǔ)上,從物體的表面過(guò)渡到平面圖形,認(rèn)識(shí)平面圖形的大小,完善面積的含義。最后通過(guò)對(duì)平面圖形面積大小的比較,強(qiáng)化對(duì)面積含義的認(rèn)識(shí)。教學(xué)面積單位時(shí),先引導(dǎo)學(xué)生產(chǎn)生統(tǒng)一面積單位的需要,再建立1平方厘米、1平方米和1平方分米的表象。最后在估測(cè)、拼擺等活動(dòng)中,深化對(duì)面積單位的認(rèn)識(shí)。
2、在探索中歸納計(jì)算方法。
教學(xué)平面圖形的面積時(shí),主要應(yīng)用的學(xué)習(xí)方式是探索性學(xué)習(xí),所以教師要通過(guò)測(cè)量、操作與推理活動(dòng),引導(dǎo)學(xué)生自主探索出計(jì)算公式。在探索的過(guò)程中,感受形的變化,發(fā)展空間觀念。如教學(xué)三角形面積的計(jì)算時(shí),例4呈現(xiàn)了3個(gè)平行四邊形,教師要引導(dǎo)學(xué)生發(fā)現(xiàn)每個(gè)平行四邊形被分成了兩個(gè)完全一樣的三角形,并說(shuō)出每個(gè)涂色三角形的面積,使學(xué)生感受到每個(gè)涂色三角形的面積是所在平行四邊形面積的一半,兩個(gè)完全一樣的三角形可以拼成一個(gè)平行四邊形,為下面的探索活動(dòng)提供思路。例5重點(diǎn)探索三角形與拼成的平行四邊形的聯(lián)系,要引導(dǎo)學(xué)生從第127頁(yè)上選一個(gè)三角形剪下來(lái),與例題中相應(yīng)的三角形拼成平行四邊形,并求出拼成的平行四邊形與每個(gè)三角形的面積。再通過(guò)討論兩個(gè)三角形與拼成的平行四邊形的關(guān)系,推理出三角形面積的計(jì)算公式。通過(guò)分類研究,使學(xué)生經(jīng)歷不完全歸納的探索過(guò)程,體現(xiàn)歸納活動(dòng)的合理性。
3、在反思中提升數(shù)學(xué)思想。
反思即在教師的引導(dǎo)下,系統(tǒng)回顧整個(gè)學(xué)習(xí)活動(dòng)過(guò)程,把探索過(guò)程中零散的、初步的認(rèn)識(shí)加以整理和升華。對(duì)學(xué)生的認(rèn)知過(guò)程再認(rèn)知,對(duì)學(xué)生已獲得的數(shù)學(xué)經(jīng)驗(yàn)再體驗(yàn),從中感受數(shù)學(xué)思想方法和策略。在教學(xué)平面圖形的面積計(jì)算時(shí),教師要經(jīng)常引導(dǎo)學(xué)生反思:“我運(yùn)用了什么方法探索?”“為什么可以用這個(gè)方法?”“探索平面圖形面積計(jì)算方法的共同點(diǎn)是什么?”如教學(xué)平行四邊形面積的計(jì)算時(shí),在每道例題教學(xué)后,都要引導(dǎo)學(xué)生進(jìn)行反思。教學(xué)例1后要引導(dǎo)學(xué)生思考:遇到不規(guī)則圖形,怎樣比較它們面積的大小比較簡(jiǎn)單?教學(xué)例2后要引導(dǎo)學(xué)生思考:怎樣把平行四邊形轉(zhuǎn)化成長(zhǎng)方形?教學(xué)例3后要引導(dǎo)學(xué)生思考:怎樣得到平行四邊形面積的計(jì)算公式?再如教學(xué)多邊形面積的計(jì)算整理與復(fù)習(xí)時(shí),要抓住核心問(wèn)題引導(dǎo)學(xué)生思考:平行四邊形、三角形和梯形面積公式的推導(dǎo)過(guò)程有什么相同的地方?在反復(fù)的體驗(yàn)和反思中,感受轉(zhuǎn)化思想。
4、在應(yīng)用中積累數(shù)學(xué)經(jīng)驗(yàn)。
學(xué)生自主探索出計(jì)算公式后。還要能應(yīng)用計(jì)算公式解決一些簡(jiǎn)單的實(shí)際問(wèn)題,在應(yīng)用的過(guò)程中。形成數(shù)學(xué)技能,積累活動(dòng)經(jīng)驗(yàn),掌握解題策略。如多邊形面積的計(jì)算單元安排了實(shí)踐活動(dòng)校園的綠化面積,教師要引導(dǎo)學(xué)生在計(jì)算組合圖形的面積中,掌握割、補(bǔ)的方法,體驗(yàn)解題策略的靈活、多樣,學(xué)會(huì)選擇合理的策略解決問(wèn)題,在將復(fù)雜圖形轉(zhuǎn)化成簡(jiǎn)單圖形的過(guò)程中,體驗(yàn)形的變化,逐步發(fā)展空間觀念。

