談圖形語言在小學數學學習中的作用
王 珍
數學競賽,有一道題:“慶元旦布置班級,小紅把16盞彩燈平均掛成4行,每行掛5盞,可以怎樣掛?(畫出圖)”全班竟沒有一個人做對,事后我做了了解,原來是學生對題目要求的畫圖解決感到納悶,不知如何下手,這一現象引起了我的思考和探究的興趣。
上世紀90年代,美國學者進行中美小學數學教育比較研究,出過這樣一道測試題:兒童分蛋糕。7個女孩平分2個,3個男孩平分1個糕。每個女孩分得多還是每個男孩分得多?每種方法可以用數字或圖形來解釋。我國被試的孩子有90%用比較分數2/7與1/3大小的方法來解釋,而美國用這種方法的僅有21%;被試的美國孩子有57%利用圖形解釋,而我國只有6%。其中有一種結合圖形解釋,非常巧妙:如果女孩只有6個,那么每個女孩與每個男孩分得一樣多,但女孩有7個,所以每個女孩比每個男孩分得少。在這樣的數學思考中,很自然地應用了“對應”的數學思想。
看來,我們的學生確實不善于用圖形語言學習、思考、表達與交流數學。圖形是數學學習的對象,也是數學交流的工具。尤其在兒童數學教育的啟蒙階段,圖形語言的地位與作用舉足輕重,是不可替代的。
如下圖形語言(□代表雞,○代表鴨)相應的:
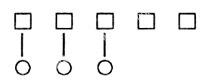
文字語言是“5比大3。”或者“3比5小。”
符號語言是“5>3,讀作:5大于3。”或者“3<5,讀作:3小于5。”
由此可見,描述數學事實、概念或關系時,圖形語言的描述為文字語言或符號語言的描述提供了直觀表象,也為理解和掌握相關的文字語言與符號語言的意義和內涵奠定認知基礎。
再如,與如下圖形語言(△代表猴,○代表鴨)相應的:
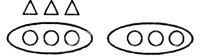
文字語言是“鴨的只數是猴的2倍。”符號語言是“6÷3=2。”
用圖形語言描述現實情境的數量關系,是對現實世界數量關系的一次抽象;符號語言是借助圖形語言的直觀對現實世界數量關系的再一次抽象;而文字語言能夠明確界定圖形語言或符號語言所描述的數學對象的意義與內涵。
圖形語言是發展學生抽象思維,理解和把握符號語言的扶梯。如果學生不能理解符號語言,進行抽象思維的時候,最好的選擇是回到圖形,甚至回到更具體的操作。
對于一個數的幾倍是多少,幾乎所有的學生都會很快反應是用乘法。新接一個班,發現一位新生對于這部分的知識反映就是不靈敏,似乎對這部分知識的認知在她腦中形成一個盲點,于是在邊與她的補課及全班的復習回顧中,發現其實不少同學是知其然而不知其所以然。
比如讓學生完成:紅花朵數(8朵)是黃花(2朵)的幾倍?請用畫圖和列式兩種方法解答。一位學生走上黑板畫了如下的圖形并列出算式如下:
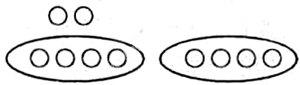
8÷2=4
答:紅花朵數是黃花的4倍。
顯然,上述的圖解是錯誤的。正確的圖解是:

圖解不對,列式正確。這是什么原因呢?看來這個學生并沒有真正理解“倍”的含義,但他卻從形式上記住了“求幾倍”的算法。事實上,不少學生學習數學都帶有這種機械學習和形式主義的特征。這是我們老師要幫助他們努力克服的。學習數學不能靠生搬硬套、死記硬背;能否自如地從一種語言轉換為另一種語言進行數學描述,能否用圖形語言解釋文字語言或符號語言,是理解數學的試金石。
在這以后我在新授這部分知識時,重視圖形語言的幫助理解,然后慢慢過度到文字語言。比如學習“求一個數是另一個數的幾倍”,先是讓學生通過操作理解“求一個數是另一個數的幾倍”
第一個問題,要知道小貓的只數是小狗的幾倍,先想什么?(用弧線表示)
第二個問題:小狗跑來2只,這時小貓的只數是小狗的幾倍?為什么?
第三個問題,小狗跑走3只,這時小貓的只數是小狗的幾倍?為什么?
第四個問題:小狗全部跑走,這時說小貓的只數是4倍,對嗎?為什么?
圖形語言的內涵是豐富的,同一個圖形可能有不同的解釋,表征不同的意義。請看下面的圖形(○代表蘋果):
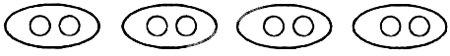
這個圖形可以解釋為8個蘋果放在4個盤子里,平均每個盤子放2個;也可以解釋為每個盤子放2個蘋果,8個蘋果可以放4盤。這兩種都是“平均分”。按前一種解釋,列的算式是8÷4=2(個);后一種解釋,算式是8÷2=4(盤)。
圖形語言也有它明顯的局限性,它受時空的制約。比如問題是“100是2的幾倍?”就不好用圖解的方法來解答了,這時列出算式計算就顯得便捷。只有掌握符號語言才能彌補和超越圖形語言的局限性,才能自由地馳騁于數學王國。但是切不可因此而輕視圖形語言賦與人的想象力和創造性,何況它還是掌握符號語言,發展抽象思維不可逾越的途徑。所以數學教師自身首先要加強圖形語言意識,并在教學中引導和鼓勵,才能使學生善于用圖形語言思考、表達與交流數學。
作者單位:廈門外國語學校海滄附屬學校

