2010年全國卷Ⅰ壓軸題中的“多種圓”
陳憑心
(安徽靈璧中學,安徽靈璧 234200)
2010年全國卷Ⅰ壓軸題中的“多種圓”
陳憑心
(安徽靈璧中學,安徽靈璧 234200)

圖1
2010年普通高校招生全國卷Ⅰ第26題:如圖1,在0≤a區域內存在與xy平面垂直的勻強磁場,磁感應強度的大小為B.在t=0時刻,一位于坐標原點的粒子源在xy平面內發射出大量同種帶電粒子,所有粒子的初速度大小相同,方向與y軸正方向的夾角分布在0~180°范圍內.已知沿y軸正方向發射的粒子在t=t0時刻剛好從磁場邊界上
P(3a,a)點離開磁場.求:

(2)此時刻仍在磁場中的粒子的初速度方向與y軸正方向夾角的取值范圍;
(3)從粒子發射到全部粒子離開磁場所用的時間.
題給條件:在t=0時刻,一位于坐標原點的粒子源在xy平面內發射出大量同種帶電粒子,所有粒子的初速度大小相同,方向與y軸正方向的夾角分布在0~180°范圍內.由條件知,所有粒子的初速度矢量未端在以O為圓心的圓上,故此圓稱為“矢端圓”,見圖2中圓O.

圖2
由“已知沿y軸正方向發射的粒子在t=t0時刻剛好從磁場邊界上P(3a,a)點離開磁場”,題中雖然未給出磁場方向及粒子電性,但由沿y軸正方向發射的粒子打到P點,剛發射時該粒子所受洛倫茲力必沿x軸正方向,圓心必在x軸上,在x軸上以某點為圓心,以適當長度為半徑作圓OP過O、P點,可稱作“軌跡圓”,由于此圓是由題給條件作出,亦可稱“條件圓”,其他所有粒子軌道半徑與其相等,環繞方向與其相同.
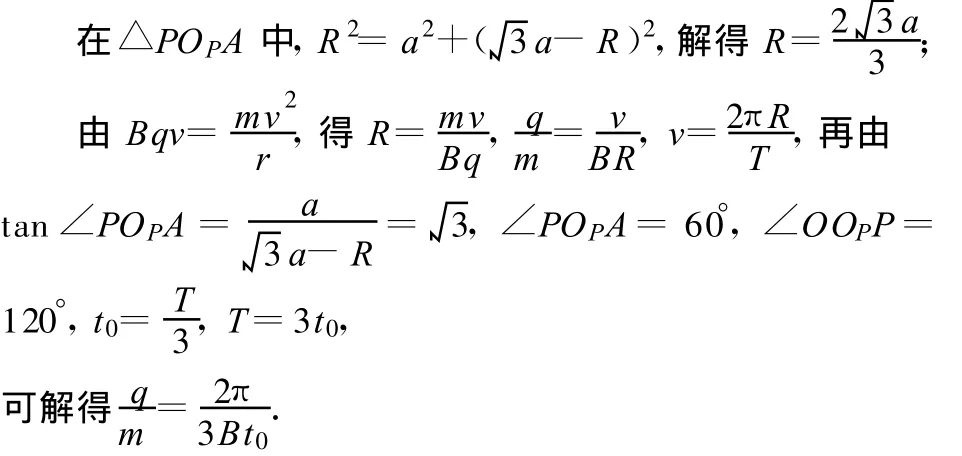
由于所有粒子都從O點開始作勻速圓周運動,且軌道半徑相等,故所有粒子作圓周運動的圓心,都在以O為圓心,R為半徑的圓上,此圓稱之為“圓心圓”.隨發射出的粒子與y軸正方向夾角不斷增大,粒子作圓周運動的圓心也由OP點在圓心圓上順時針移動,可在圖2中作出一系列“動態圓”,這些粒子分別從P1…P4點穿出磁場右邊界.
t0時刻仍在磁場中的粒子,與打到P點的粒子相比,應該在相同的時間內走過的弧長相等,對應的弦長度相等,即該時刻在磁場中的粒子到O點的距離相等,即在以O為圓心,以OP為半徑同一時刻“位置圓”上.

圖3
t0時刻在位置圓上MN上的粒子仍在磁場中,其圓心在圓心圓上自OM至ON之間的O5、O6等位置,其軌跡如圖 2中的圓OM、O5、O6、ON等一系列動態圓;在這些動態圓中,M、N是在磁場中的臨界位置,圓OM、ON為“臨界圓”,因P、M關于x軸對稱,∠OOMM=∠OOPP= 120°,OOM⊥OOP,且速度方向與半徑垂直,打到M點的粒子初速度沿OP方向,與y軸正方向夾角60°,又∠OONN=120°,∠ONON=30°,vN⊥OON,與y軸負方向夾角為60°,與y軸正方向夾角為120°,故t0時刻仍在磁場中的粒子的初速度與y軸正方向夾角為60°≤θ≤120°.

2010-07-06)

