基于可靠性技術的汽車鋼板彈簧設計

趙建平

（南京理工大學紫金學院，江蘇南京210046）

鋼板彈簧作為影響車輛安全的重要零件之一，既負責傳遞所有各向力和力矩，還具有彈性元件、減振器和導向機構的特性，是重要的高負荷安全部件[1]。近年來，國內外學者對鋼板彈簧的設計進行了研究。王其東[2]等利用虛擬樣機理論，在整車動力學仿真的基礎上，對汽車鋼板彈簧的結構參數進行了優化設計，并對鋼板彈簧進行了有限元分析；林開榮[3]利用模糊數學理論和優化設計方法，建立了基于模糊綜合評判的汽車鋼板彈簧優化設計的數學模型，并探討了其優化設計方法；滕瑛瑤[4]等分析了彈簧材料、加工工藝、設計參數和使用條件對汽車鋼板彈簧疲勞壽命的影響，為鋼板彈簧的設計提供了一定的理論依據。上述文獻中，可靠性設計在汽車鋼板彈簧設計中的研究較少，而現今鋼板彈簧可靠性日益受到關注，其設計和制造水平也提出了較高的要求。

1 可靠性設計基本理論和方法

所謂可靠性，是指產品在規定的時間內和給定的條件下，完成規定功能的能力。它不但直接反映產品各組成部件的質量，而且還影響到整個產品質量性能的優劣。事實上，可靠性設計所要解決的問題，就是如何從設計中入手，來解決產品的可靠性，以改善對各個零部件可靠度的要求，而可靠度的分配是可靠性設計的核心。零部件的載荷、幾何尺寸、材料性能等都是隨機變量，是某種概率分布的統計量。可靠性設計正是考慮設計參數的分散性，在常規設計公式的基礎上，引入了可靠度或其他可靠性指標，不單純用一個安全系數來衡量零件的強度，用概率統計的方法來處理各個設計變量，同時對系統失效的可能性進行定量分析和預測。

常規設計方法中，滿足強度的判據為：零件的強度必須大于工作壓力。可靠性設計的目標是：零件強度h大于工作壓力S的概率，要大于或等于所要求滿足的可靠度R。當已知概率密度函數或聯合概率密度函數，且極限狀態方程中的變量都是正態變量時，可靠性指標和可靠度很容易求得。若含有非正態變量時，只要進行等效正態變換，也容易求得可靠性指標和可靠度。但在工程實踐中，往往很難有足夠的資料來確定隨機變量的概率密度函數或聯合概率密度函數，而要確定它們的一階矩和二階矩(即均值、方差和協方差)卻較容易，故可先求它們的一階矩和二階矩，再用二階矩法求可靠性指標和可靠度[5]。

2 汽車鋼板彈簧的可靠性設計

某型汽車鋼板彈簧的已知參數如下：

鋼板寬度（μb，σb）=（70，0.35）mm；

鋼板長度（μl，σl）=（1 100，5.5）mm；

鋼板彈簧厚度（μh，σh）=（6.5，0.032 5）mm；

車身載荷（μp，σp）=（5 537，276.85）N；

材料強度（μr，σr）=（614，45.8）MPa；

鋼板片數n=6。

2.1 鋼板彈簧的參數確定

（1）滿載弧高fα。fa用來保證汽車具有給定的高度。當fa=0時，鋼板彈簧在對稱位置上工作。考慮到使用期間鋼板彈簧塑性變形的影響，和為了在車架高度已限定時能得到足夠的動撓度值，文中選取fa=15 mm。

（2）鋼板彈簧長度L1。鋼板彈簧長度L1是指彈簧伸直后兩卷耳中心之間的距離。選用長一些的鋼板彈簧，會在汽車上布置時產生困難。在總布置可能的條件下，應盡可能將鋼板彈簧取長一些。文中L=1 100 mm，是包括卷耳及包耳邊界的尺寸長度，所以L1=825 mm。

（3）鋼板斷面寬度b。有了鋼板彈簧的平均厚度hp以后，再選鋼板彈簧的片寬b。鋼板彈簧的平均厚度hp可在下式計算得到。

式中，U型螺栓中心距s為120 mm；

k為考慮U型螺栓夾緊彈簧后的無效長度系數，取k=0.5；

c為鋼板彈簧垂直剛度（N/mm），c=Fw/fc；

δ為撓度增大系數δ=1.33；

E為材料的彈性模，E=2.1×105MPa；

代入式（1）中，求得hp=3.5 mm，b=70 mm。

（4）鋼板彈簧片厚h。將計算得平均厚度hp=3.5 mm，代入式(2)，

計算得厚度h2=5mm，為使各片壽命接近，又要求最厚片與最薄片厚度之比小于1.5，經驗算，6.5/5=1.3＜1.5，驗算合格。

（5）鋼板彈簧各片長度。根據鋼板彈簧長度計算公式：

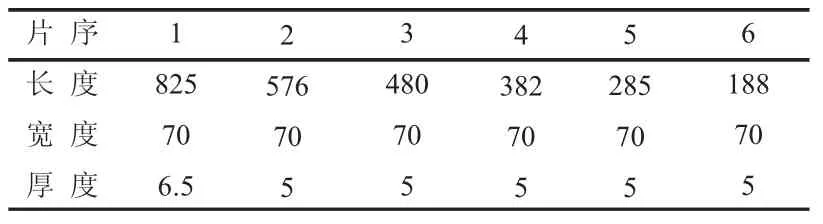
表1 各片鋼板彈簧的基本尺寸單位：mm

2.2 可靠性設計

汽車的多片鋼板彈簧，多半為中心受載的簡支疊板彈簧，其工作應力為

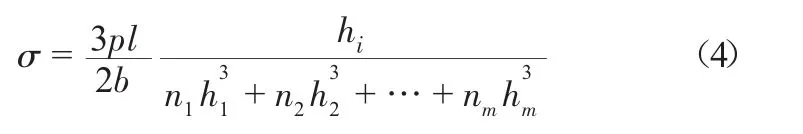
式中，p為載荷；幾何尺寸寬度、厚度和跨距分別為b、hi和l；ni為鋼板片數。

本文中，載荷 p=5 537 N，b=70 mm，h1=6.5 mm，h2=5 mm，l=1 100 mm，將hmax=7.3 mm代入式(4)，經過計算得 σmax=39.7 MPa。

根據應力—強度干涉理論，以應力極限狀態表示的狀態方程為

式中，r為鋼板彈簧的材料強度；基本隨機變量向量，其均值E(x)和方差及協方差Var(x)為已知，并且隨機變量是服從正態分布相互獨立。g(x)為狀態函數，是反映鋼板彈簧的狀態和性能的，可表示鋼板彈簧的兩種狀態：

g(x)≤0為失敗狀態；

g(x)>0為安全狀態。

已知彈簧材料強度r=45.8 MPa，由式5計算得g(x)=r-σmax=45.8-39.7=6.1 MPa＞0，因此，鋼板彈簧屬于安全狀態，可靠性驗證成功。

把狀態函數g(x)在隨機變量向量x的均值E(x)=x軃處展開成二階Taylor級數，根據的g(x)均值和方差的表達式，可求g(x)的均值和方差，然后再代入可靠性指標和可靠度的表達式，就能確定可靠性指標和可靠度。可靠性指標定義為

式中，μg為二階近似均值，σg為一階近似方差。

給定鋼板彈簧的可靠性指標β=3.377，可查得可靠度R=0.999 6，根據加工公差和3σ法則，取鋼板彈簧設計處的厚度h的標準差為σA，即可求鋼板彈簧的最小厚度h的均值和標準差。

2.3 可靠性設計計算軟件的開發

本可靠性設計計算軟件在Windows XP中文系統環境下，采用面向對象程序設計語言工具Visual Basic進行開發。適用于普通汽車懸掛系統鋼板彈簧可靠性設計與計算[6]。其程序流程圖如圖1所示。

汽車鋼板彈簧可靠性設計計算軟件應用的用戶界面，如圖2所示。它的生成依賴于其調用程序，可以直接輸入所設計彈簧的基本懸掛指標。其中，已知滿載質量為3.5 t，簧下質量為0.8 t，可靠性指標β=3.377，可靠度R=0.999 6，滿載弧高fa=15 mm，板簧長度L=1 100 mm，板簧寬度b=70 mm；板簧片數n=6。點擊“可靠性設計”，程序會計算出“板簧片厚h(mm)”和“各片長度 Li(mm)”，隨后點擊“可靠性驗證”按鈕，對設計計算出的數據進行驗證，驗證界面如圖3所示。

圖2 用戶界面圖

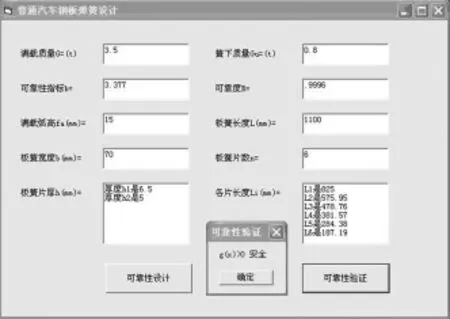
圖3 用戶驗證界面

由圖3可知，運用本文的軟件設計計算方法，在滿足可靠度要求的同時，精確計算出各鋼板彈簧的厚度和長度，從而使鋼板彈簧的設計計算較方便。數據輸人快捷，數據存取容易，計算速度快，計算精度較高，能滿足一般鋼板彈簧可靠性設計計算要求。

3 結束語

隨著汽車業界競爭的日益加劇，都在力求在保證產品質相短路故障持續0.1 s后切除，采用模糊控制的發電機端電壓比采用傳統PID控制的發電機端電壓反應速度更快。

圖7中實線部分為模糊控制的控制效果，虛線部分為傳統PID的控制效果。如圖7所示，發電機的角速度發生變化，三相短路故障持續0.1 s后切除，模糊控制能夠使角速度變化量更快地回到零點，使系統穩定。

4 結束語

本文利用模糊控制對同步發電機進行控制，具有良好的勵磁調節特性。模糊控制取代傳統PID控制，可以有效地提高電力系統響應速度。通過仿真實驗可以看出，在單機無窮大系統中，對于采用模糊控制的同步發電機，可以達到優于傳統PID控制的效果，具有良好的前景。

[1]Wenxin Liu,G.K.Venayagamoorthy,and D.C.Wunsch.Design of Adaptive Neural Network Based Power System Stabilizer[J].Neural Networks，2003，(16)：891-898.

[2]Salman Mohagheghi,G.K.Venayagamoorthy,Ronald G.Harley.Adap tive Critic Design Based Neuro-Fuzzy Controller for a Static Compen sator in a Multimachine Power System[J].Power Systems，2006，(21)：1744-1754.

[3]王紅君，趙 輝，華 巖．模糊參數自適應PID控制器在同步發電機勵磁系統中的應用[J]．電氣傳動，2000，30(2)：37-40.

[4]喬志杰，王維慶．模糊自適應控制器的設計及其仿真[J]．控制系統，2008，(1)：26-29.

[5]韓唆峰，李玉惠．模糊控制技術[M]．重慶：重慶大學出版，2003．

[6]廉小親．模糊控制技術[M]．北京：中國電力出版社，2003．