不同流場中雙層圓柱殼層間聲振傳遞特性研究

高 菊 陳美霞 陳清坤 和衛(wèi)平

華中科技大學船舶與海洋工程學院，湖北武漢 430074

不同流場中雙層圓柱殼層間聲振傳遞特性研究

高 菊 陳美霞 陳清坤 和衛(wèi)平

華中科技大學船舶與海洋工程學院，湖北武漢 430074

采用解析法研究了不同流場中雙層圓柱殼層間聲振傳遞特性。殼體的振動用Flügge殼體方程描述，將加強構件等價為對內(nèi)外殼體的支持力，最后求解雙殼體聲—流體—結構耦合方程，計算結果用表面振動均方速度級、輻射聲功率和輻射效率的形式表示。在數(shù)值分析部分，討論了有限長雙層圓柱殼殼間連接形式的變化、殼間及外部流場的變化對其聲輻射性能的影響，得到結論是在中低頻段，當內(nèi)殼受激振動，通過外殼向外場輻射噪聲時，其主要通道為連接內(nèi)外殼殼體的實肋板，其次才是環(huán)形流場中的流體介質(zhì)。

有限長雙層圓柱殼；流場；實肋板；振動；聲輻射

1 引言

雙層圓柱殼是一種常見的工程結構，經(jīng)常用于模擬潛艇的典型艙段。陳越澎等［1］基于Flügge殼體理論和Helmholtz波動方程計算并分析討論了殼間充滿流體的有限長雙層圓柱殼在受徑向點激勵下的振動與聲輻射性能，但其研究的圓柱殼模型內(nèi)外殼間無連接構件，與實際情況不符。曾革委［2］研究了實肋板連接的雙層加肋圓柱殼水下聲輻射，研究了舷間流體對內(nèi)外殼板的壓力以及實肋板對內(nèi)外圓周殼板的作用力，并得到了內(nèi)外殼體耦合振動控制方程。陳美霞等［3］研究流場中受徑向點激勵的有限長雙層圓柱殼殼間用實肋板連接或用托板連接對其振動和聲輻射性能的影響，但是并沒有考慮不同流場的介質(zhì)的影響程度。殷學文等［4］研究了兩個同心圓柱殼體間通過周期環(huán)板和附連流體的耦合效應，其在環(huán)板內(nèi)只有準縱波存在的假定下，給出環(huán)板的反作用力的表達式，并建立外殼體的聲輻射解析表達式，但忽略了環(huán)板的面內(nèi)彎矩及面外力。本文在求解計算時考慮了實肋板的面內(nèi)力及面外力，并針對雙層殼間有無實肋板連接、殼間及外殼外部流場進行了分析。

在實際結構中，雙層圓柱殼的層間充滿了流體水，兩層殼間由實肋板、托板等構件連接在一起；雙層殼浸沒在流體水中。當雙層圓柱殼的內(nèi)殼受激振動時，其振動與聲輻射要經(jīng)由復雜的層間結構及流場由內(nèi)殼傳遞到外部流場中。為了更好的分析振動與聲傳遞的途徑，本文以Flügge殼體理論為基礎，通過解析法計算結果分析雙層圓柱殼層間聲振傳遞的特性。

2 基本方程

2.1 計算模型

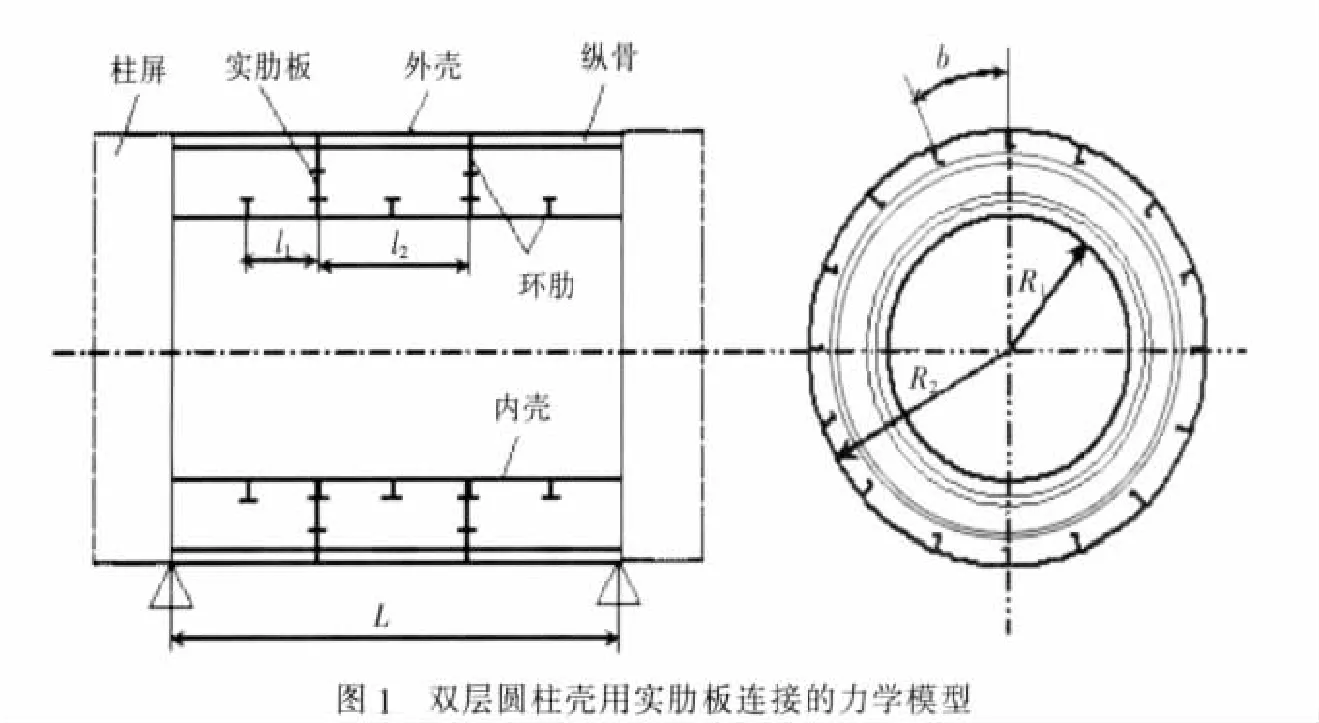
本文所采用的模型為浸沒在無限流場中的有限長加筋雙層圓柱殼，計算求解采用柱坐標系，殼體的幾何參數(shù)如圖1所示。圖中，l1為內(nèi)殼外環(huán)肋間距，l2為實肋板間距及外殼內(nèi)環(huán)肋間距，A1、A2分別為內(nèi)殼外環(huán)肋和外殼內(nèi)環(huán)肋的橫截面積，b為外殼上縱骨周向間距，R1為內(nèi)殼半徑，R2為外殼半徑。假設雙層圓柱殼兩端連接有無限長剛性障板，結構響應在線性范圍內(nèi)，流體滿足線性聲學條件。

2.2 雙層殼體結構—聲—流體耦合方程

雙層圓柱殼運動采用Flügge殼體理論描述，將環(huán)肋、實肋板和縱骨視為動反力作用在殼體上，其振動方程為：

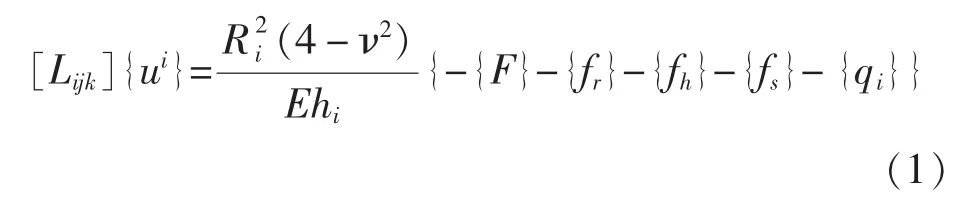
式中，［Lijk］（i＝1，2 分別代表內(nèi)、 外層殼體； j，k ＝1，2，3）為采用 Flügge 理論的殼體微分算子，慣性項和靜水壓力項均包含在內(nèi)，其具體表達式見式（2）；｛ui｝＝｛uiνiwi｝T表示殼體軸向、 周向和徑向位移；｛F｝為作用在殼體上的激勵力；｛fr｝為環(huán)肋的反力［5］；｛fh｝為縱骨的反力［6］，｛fs｝為實肋板反力（對于殼間無實肋板的結構， 則無此項）；｛qi｝＝｛0 0 qir｝T為輻射聲壓。本文主要研究殼間連接形式的變化、殼間及外部流場的變化，因此下文著重分析振動與聲輻射的傳遞途徑。

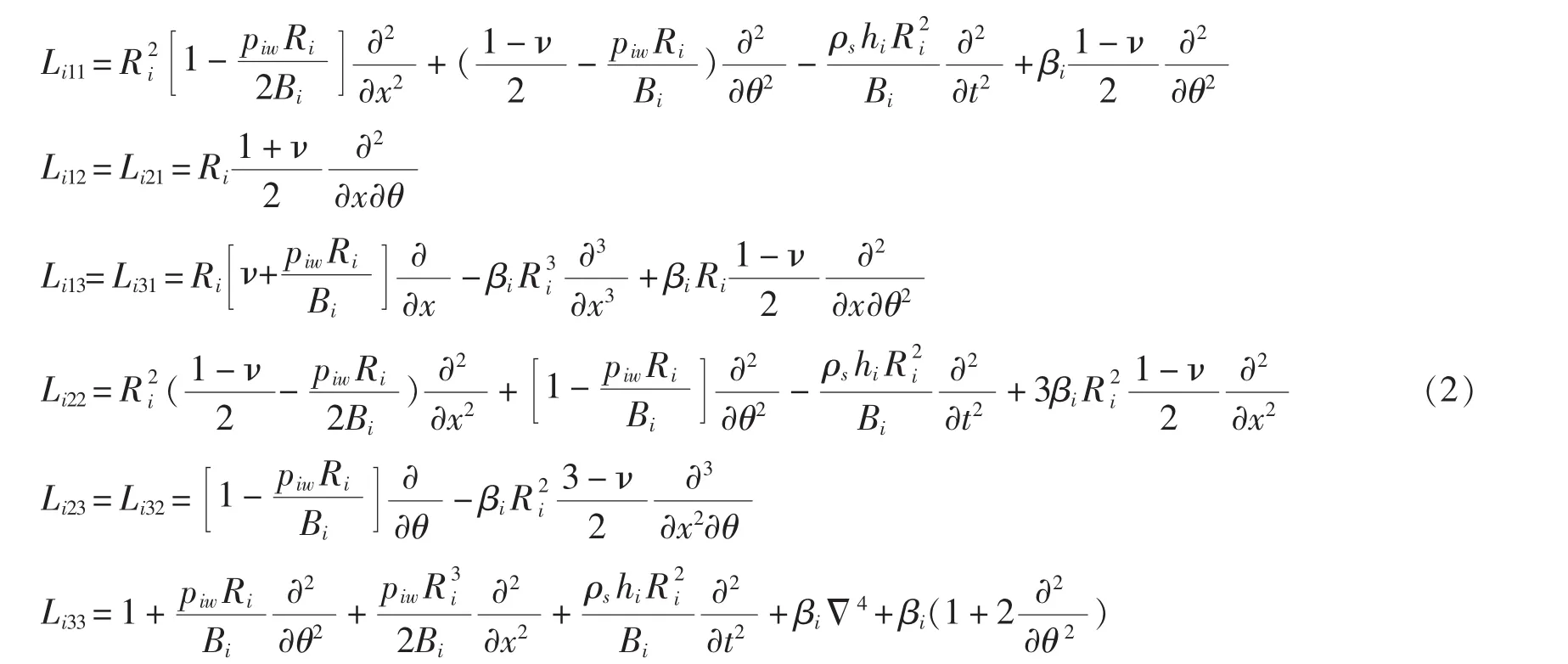
2.3 雙層圓柱殼振動波傳遞途徑

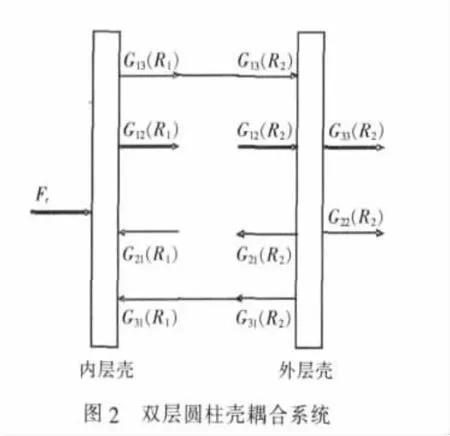
當內(nèi)殼受到激勵時其振動波由內(nèi)殼傳遞到外部流場中的傳遞途徑有2種，如圖2所示。

2.3.1 通過環(huán)形流場傳遞

內(nèi)殼振動波G12（R1）通過環(huán)形流場流體介質(zhì)傳播到外殼并激勵外殼，與此同時產(chǎn)生反向波G21（R2），通過環(huán)形流場向內(nèi)殼傳遞 G21（R1），并激勵內(nèi)殼振動［7］。這種正向波和反向波產(chǎn)生相互耦合作用，時而抵消時而加強，最后通過外殼振動向外場輻射 G22（R2）聲波。

2.3.2 通過實肋板傳遞

實肋板將內(nèi)外殼體連接起來［8］，當內(nèi)殼受激振時，振動波G13（R1）通過實肋板傳向外殼并激勵外殼振動G13（R2），同樣外殼振動時產(chǎn)生反向激勵，通過實肋板返回到內(nèi)殼即G31（R1），相互耦合后再通過外殼向外場輻射G33（R2）。

由于實肋板的振動狀態(tài)及其復雜，可將實肋板的彎曲振動與伸縮振動看成是解耦的［9］，從而分別研究實肋板的這2種振動形式。

1）實肋板的伸縮振動

將實肋板的伸縮振動看作面內(nèi)運動，將其當做平面應力問題來處理。在極坐標系中實肋板的振動方程［10］為：

實肋板與圓柱殼連接處的徑向和周向反力如下所示：

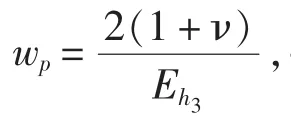
2）實肋板的彎曲振動

實肋板的彎曲振動方程為：

式中，｛fisk｝表示殼體（i＝1 表示內(nèi)殼，i＝2 表示外殼）上第k個實肋板的反力向量；xk為實肋板的軸向位置，Ns表示實肋板軸向的個數(shù)。

3 數(shù)值計算結果與分析

計算采用的雙層圓柱殼的幾何參數(shù) （其中R1、 l1、R2、 l2、b、 A1、 A2含義如前所述） 具體為：R1／h1＝ 125，R1／l1＝ 5.83，R1／L ＝ 0.36，R2／h2＝ 430，R2／l2＝ 3.58，R2／L ＝ 0.45； h1、h2分別為內(nèi)層殼體及外層殼體的厚度；L為雙層圓柱殼的總長；縱骨為 Γ10，b＝10°；內(nèi)殼環(huán)肋為 A1／（l1h1）＝0.332，外殼環(huán)肋為 A2／（l2h2） ＝0.288； 雙層圓柱殼浸沒在無粘無旋可壓縮的無限外流場中。殼體、環(huán)肋、縱骨、實肋板的材料相同，密度為 ρs＝7 850 kg／m3，彈性模量 E ＝2.1 ×1011N／m2，泊松比 ν ＝0.3，損耗因子為 η＝0.01。 水的密度為 ρw＝1 000 kg／m3，水中聲速為c0＝1 500 m／s。 徑向簡諧力激勵作用在內(nèi)殼（L／2，0）處，幅值為 1 N。當殼間有實肋板連接時，實肋板沿軸向等間距分布，厚度為h3＝ h2。

聲輻射性能用振動均方速度、輻射聲功率和輻射效率來表示，其中均方振速級和聲功率級的基準分別為：V0＝1.0 ×10－9（m／s），W0＝ 1.0 ×10－12（W）。

本文采用自行編程進行計算，基于殼間連接方式、殼間及外部流場介質(zhì)屬性共討論了8種情況下殼體振動和聲輻射的響應：

1）殼間無實肋板連接情況下的4種模型：殼間及外部流場介質(zhì)為水（A模型）；殼間及外部流場介質(zhì)為空氣（B模型）；殼間流場介質(zhì)為空氣而外部流場介質(zhì)為水（C模型）；殼間流場介質(zhì)為水而外部流場介質(zhì)為空氣（D模型）。

2）殼間有實肋板連接情況下的4種模型：殼間及外部流場介質(zhì)為水（E模型）；殼間及外部流場介質(zhì)為空氣（F模型）；殼間流場介質(zhì)為空氣而外部流場介質(zhì)為水（G模型）；殼間流場介質(zhì)為水而外部流場介質(zhì)為空氣（H模型）。

3.1 殼間無實肋板連接時流場介質(zhì)對雙層圓柱殼振動與聲輻射的影響

圖3所示為殼間無實肋板連接時殼間及外殼外部流體分別為水及空氣情況下的雙層圓柱殼的內(nèi)外殼表面振動速度級、輻射聲功率級和輻射效率對比曲線。

圖3（a）所示為內(nèi)殼均方振速級曲線，A與D、B與C模型的曲線趨勢分別相似，即在殼間流體介質(zhì)相同的情況下，內(nèi)殼均方速度曲線變化趨勢相同。在頻率小于150 Hz時，D曲線與A模型曲線的變化趨勢相同，并且相同變化趨勢處速度級大小相近，但D曲線比A曲線整體向右偏移，由于在較低頻率，外流場對殼體的影響較大，A模型外流場為水，D模型外流場為空氣，因此D模型的固有頻率要偏高；在頻率大于150 Hz時，D曲線與A曲線變化趨勢基本相同，多數(shù)頻率下，兩者數(shù)值相差較小；在整個計算頻率段，B模型與C模型的內(nèi)殼振動速度曲線基本重合，由于兩者層間流體均為空氣，空氣傳遞振動能量弱，此時外部流場對內(nèi)殼的影響不大；在整個計算頻率段，總體上B與C模型數(shù)值要大于A與D模型數(shù)值，并且B與C出現(xiàn)第一峰值的頻率比A與D的高。圖3（b）為外殼均方振速級曲線，由于此時殼間僅有流場傳遞振動，而流體介質(zhì)水傳遞的能量要遠遠大于介質(zhì)空氣傳遞的能量，因此在整個計算的頻率范圍內(nèi)，各曲線的數(shù)值大小關系為：D＞A＞B＞C，由此可見內(nèi)流場比外流場對外殼的均方振速影響要大；外殼外部為無限流場，外殼外部流體對外殼施加壓力，起到一定的抑制殼體振動的作用，由于水的密度遠大于空氣，其對外殼振動的抑制作用更強，因此在層間流場相同的情況下，外殼外部流場為水時，外殼的振動要弱。圖3（c）為輻射聲功率級曲線，在整個計算的頻率范圍內(nèi)，A＞D＞B＞C，這主要是由于此時殼間僅有流場傳遞振動，而介質(zhì)水傳遞的能量要遠遠大于介質(zhì)空氣傳遞的能量；同樣的，外殼外部流場為水時，介質(zhì)水對聲輻射的傳遞作用更強。

由各圖可知，當雙層殼間僅有流體傳遞振動時，外殼外部流體介質(zhì)為水的模型，其輻射聲功率要大于介質(zhì)為空氣的模型。除內(nèi)殼均方速度外，殼間流體介質(zhì)對殼體的振動與聲輻射影響要大于外部流體介質(zhì)。

3.2 殼間有實肋板連接時流場介質(zhì)對雙層圓柱殼振動與聲輻射的影響

圖4所示為殼間有實肋板連接時，殼間流體分別為水及空氣情況下的雙層圓柱殼的內(nèi)外殼表面振動速度級、輻射聲功率級和輻射效率對比曲線。

圖4（a）所示為內(nèi)殼均方振速級曲線，在頻率小于100 Hz時，E、G、H曲線整體的變化趨勢相似，但G模型的曲線峰值位置要滯后E模型的曲線峰值位置；當頻率大于100 Hz時，3條曲線峰值交錯；F曲線的變化趨勢與其他三條曲線相差較大，其曲線第一個峰值出現(xiàn)在57 Hz附近，當頻率大于200 Hz時，F(xiàn)曲線的內(nèi)殼均方振速級要大于其他三條曲線。在整個計算的頻率段，H曲線的數(shù)值要大于E曲線，這是由于H模型的外流場為空氣，其對外殼體的抑制作用小，這種抑制通過實肋板作用傳遞給內(nèi)殼很小，所以其內(nèi)殼均方速度要大于E模型。E、G兩條曲線交錯。圖4（b）所示為外殼均方振速級曲線，四條曲線變化情況與圖4（a）相似。圖 4（c）為輻射聲功率級曲線，在頻率低于15 Hz時，4條曲線非常接近；頻率在15～150 Hz之間時，E與G模型兩條曲線交錯，但G模型的曲線峰值個數(shù)要少；頻率大于150 Hz時，G模型的數(shù)值要大于E模型的；在整個頻率段范圍內(nèi)，H曲線幅值基本均小于E曲線。在頻率小于200 Hz時，除個別峰值處外，F(xiàn)曲線幅值最小，當頻率大于200 Hz時，F(xiàn)曲線數(shù)值與E曲線數(shù)值相差不大，兩條曲線交錯。總之，當有實肋板連接時，外部流體介質(zhì)比殼間流體介質(zhì)對殼體的輻射聲功率影響大。

3.3 內(nèi)外殼聲振傳遞途徑分析

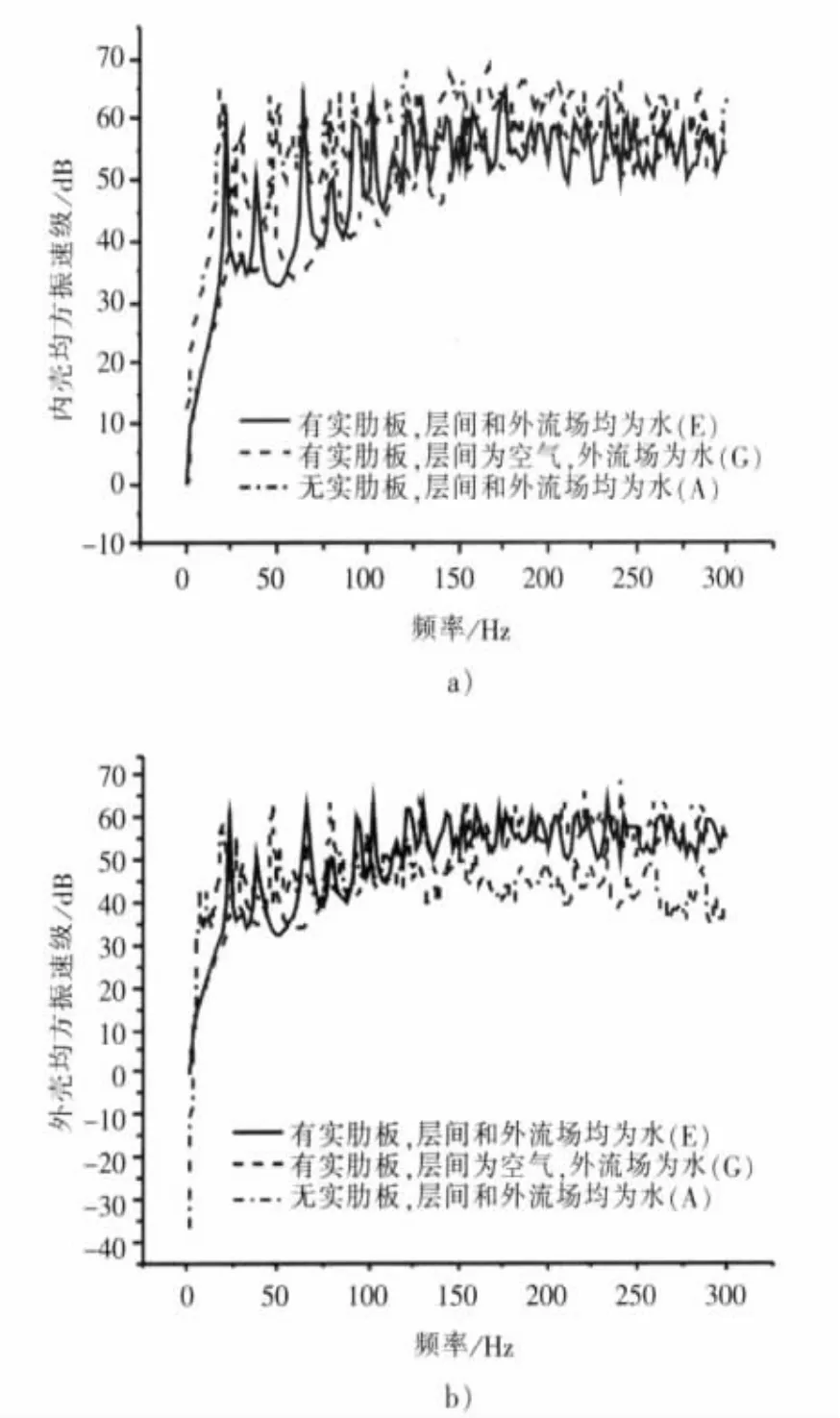
由圖5可知，在計算的大部分頻段內(nèi)，A模型的內(nèi)殼振動均方振速級大于模型E與G，這是由于連接構件的存在抑制了內(nèi)殼的振動；對于外殼均方振速級，A曲線第一個峰值所在頻率要低于另兩條曲線，當頻率在20 Hz～100 Hz之間時，三條曲線交錯，當頻率大于100 Hz時，A曲線的幅值明顯小于E與G，由此可知當殼間有實肋板連接時，從內(nèi)殼傳遞到外殼的振動能量更多，因此對外殼來說，A模型的外殼振動均方振速級反而小，且A模型的輻射聲功率級也均比另兩條曲線小。由以上分析知內(nèi)殼振動波通過殼間連接構件 （實肋板等）傳遞為主，以殼間環(huán)形流場傳遞為輔。由于殼間連接方式變化使得殼體的動力學特性發(fā)生了改變，而輻射表面沒有改變，因此殼間連接方式變化對振動的影響比對聲輻射的影響大，所以A模型的輻射效率高，如圖5（d）所示。

4 結 論

本文研究了有限長雙層圓柱殼間有無實肋板連接、殼間及外部不同流體介質(zhì)情況下，殼體的振動與聲輻射性能，所得結論如下：

1）中低頻段，當雙層圓柱殼間有實肋板連接時，振動能量主要依靠實肋板傳遞，以殼間流體傳遞為輔，不同殼間流體介質(zhì)對圓柱殼的振動和聲輻射性能影響不是很大；實際結構中均有實肋板等加強構件的支撐，因此在誤差允許范圍內(nèi)，可以忽略殼間流體介質(zhì)的影響，僅考慮外部流場的作用來研究雙層殼的振動與聲輻射性能，從而合理地簡化模型及簡化計算。

2）當雙層圓柱殼間無實肋板連接時，振動能量僅依靠殼間流體傳遞，不同殼間流體介質(zhì)對圓柱殼的振動與聲輻射性能影響很大。

［1］陳越澎，文麗，駱東平，等.流場中殼間充液雙層殼體聲輻射性能研究［J］.華中理工大學學報，1999，27（7）：83－85.

［2］曾革委.輻射噪聲的建模、求解及其聲特性研究［D］.武漢，華中科技大學，2002.

［3］陳美霞，駱東平，楊叔子.殼間連接形式對雙層殼聲輻射性能的影響［J］.振動與沖擊，2005，24（5）：77－80.

［4］殷學文，王貢獻，華宏星，等.通過周期環(huán)板和附連流體的兩同心圓柱殼體間的振動耦合效應 ［J］.聲學學報，2009，34（1）：87－95.

［5］YOSHIKAWA S，WILLAMS E G，WASHBURN K B.Vibration of two concentric submerged cylindrical shells coupled by the contained fluid ［J］.J Acoust Soc Am，1994，95（6）：3273－3286.

［6］陳越澎，駱東平，張書吉，等.環(huán)形肋板動反力分析［J］.華中理工大學學報，1998，26（12）：49－51.

［7］陳美霞.有限長加筋雙層圓柱殼聲輻射性能分析［D］.武漢，華中科技大學，2003.

［8］CHEN M X，LUO D P，CHEN X M，et al.Analytical solution of radiation sound pressure of double cylindrical shells in fluid medium［J］.Applied Mathematics and Mechanics，2002，23（4）：463－470.

［9］GUO Y P.Sound scattering by bulkheads in cylindrical shells［J］.J Acoust Soc Am，1994，95（5）：2550-2559.

［10］徐芝綸.彈性力學［M］.北京：高等教育出版社，1990.

Sound and Vibration Transmission Characteristics Between Inner and Outer Double Cylindrical Shells in Different Flow Fields

Gao Ju Chen Mei－xia Chen Qing－kun He Wei－ping
School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

The sound and vibration transmission characteristics between double cylindrical shells in different flow fields were studied with the analytical method.The Flügge equation of thin shell was applied to describe the shell vibration.By this equation， stiffening member was usually regarded as equivalent supporting force to the double cylindrical shell， and then the solution of coupled equation of sound－fluid－structure interaction was obtained.The calculated results were presented in terms of surface vibration mean－square velocity stage， radiation sound power and radiation efficiency.In the numerical analysis，the influences of connection variation between finite－length double cylindrical shells and varied flow fields of outside on the acoustic radiation performances were analyzed.The results show that in the event of the vibration noise excited by inner shell in the low or medium frequency range，the radiated noise of transmission path into the flow field of outside is mainly via the solid plates connected inner and outer shells other than the fluid medium in the annular flow field.

finite-length double cylindrical shell；flow field；solid plate； vibration； acoustic radiation

TB532

A

1673－3185（2010）05－34－06

10.3969/j.issn.1673-3185.2010.05.007

2010－01-28

國家自然科學基金資助（50805055）

高 菊（1985－），女，碩士研究生。研究方向：船舶與海洋結構物設計制造。E-mail：frank＿gr＠ 163.com

陳美霞（1975－），女，副教授。研究方向：船體結構振動及噪聲控制。E-mail：chenmx26＠ 163.com