基于運動靈活性的蟑螂機器人機構參數優化

張建斌 宋榮貴 陳偉海 張廣萍

(北京航空航天大學 機械工程及自動化學院,北京 100191)

基于運動靈活性的蟑螂機器人機構參數優化

張建斌 宋榮貴 陳偉海 張廣萍

(北京航空航天大學 機械工程及自動化學院,北京 100191)

從仿生蟑螂機器人機構特點出發,基于運動靈活性,選擇橢圓形身體布局,分別以單腿工作空間和整機雅克比矩陣的條件數倒數作為靈巧度指標,在兼顧運動靈活性和可靠性的基礎上,對機器人機構參數進行優化配置,選擇了最優的桿長比例.利用分析得出的優化尺寸建立 ADAMS參數化仿真模型進行實驗研究,仿真結果與理論分析相吻合,驗證了優化配置的可行性和正確性,為樣機的研制和機器人的驅動及控制等進一步研究奠定了基礎,也為其他六足機器人的開發提供了參考.

仿生蟑螂機器人;靈活性;優化;雅克比矩陣

仿生蟑螂機器人是基于蟑螂運動靈活穩定,對地形適應能力強等優點而開發的并聯運動機構,通常采用三角步態行進[1],具有較好的機動性,對不平路面適應能力突出,可以輕松跨過較大障礙物.因此在抗震救災、搜索救援、外星探索等領域有著廣泛的應用[2].

從機構學角度看,仿生蟑螂是一個復雜的冗余驅動多支鏈并聯機構,優化配置其機構參數,提高運動靈活性和穩定性極其重要,目前主要是采用工作空間和靈巧度進行優化[3-5].

工作空間是機器人的操作區域,是機器人運動性能的重要指標.而靈巧度則可以認為是表征機器人自主改變其位姿或方向以及傳遞力和力矩的能力[6],常用雅克比矩陣條件數和可操作度[2-3]表示.

國內外許多學者基于雅克比矩陣條件數、工作空間以及全局靈巧度指標[4]對多種機器人進行了研究[7-10].采用工作空間和基于雅克比矩陣的靈巧度指標,對機器人的結構參數進行優化配置,其結果更加可靠和準確,在體現運動靈活性的基礎上,保證了運動的準確和可靠性,同時也可以使機器人盡量遠離奇異空間.

本文從仿生蟑螂機器人的機構學特點出發,基于運動靈活性,分別以單腿工作空間和整機雅克比矩陣的條件數倒數作為靈巧度指標,對其機構參數進行優化配置.利用分析得出的優化尺寸建立了參數化模型進行仿真研究,驗證了優化配置的可行性和正確性,為樣機的研制鋪平了道路,也為其他六足機器人的開發提供了參考.

1 蟑螂機器人機體結構

蟑螂有 6條腿,對稱式分布,一般研究常用的機器蟑螂結構如圖 1a所示.機體成長方形,六足對稱分布,每條腿有 4個關節,分別為髖關節、大腿、小腿和踝關節,其中前 3個關節為驅動關節,各關節之間的連桿分別稱為基節、股節和脛節.

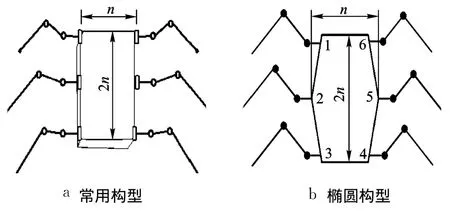
圖1 蟑螂機器人機構簡圖

實際蟑螂及大多數昆蟲的身體都不是長方形,而是呈橢圓形[11],后者運動性能更好.

圖2為等長寬比、不同結構的髖關節擺動范圍及支撐三角形,陰影部分表示髖關節可達到的轉角范圍.圖 3為支撐三角形對比,DE與 D′E′為表征機器人運動穩定性的重要指標[12]:縱向穩定裕量 SL.可以看出,橢圓形布局減少了腿的碰撞,增大了髖關節轉動范圍,提高了運動靈活性;同時明顯增大了縱向穩定裕量,提高了機器人的運動穩定性.因此,本研究中的仿生蟑螂機器人采用橢圓型的身體結構.

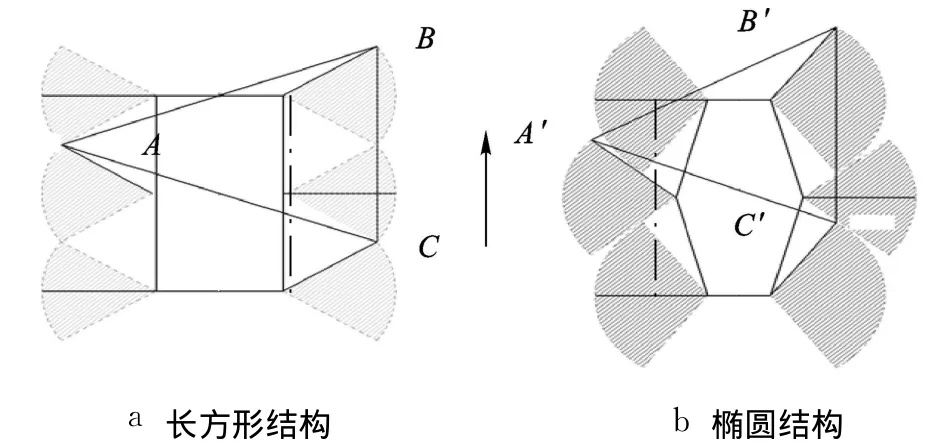
圖2 兩種結構髖關節擺角及支撐三角形

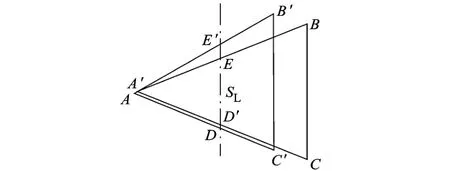
圖3 支撐三角形對比

2 基于單腿工作空間的參數優化

機器人擺動腿可視為串聯機械臂,其足端所能到達的工作空間可以參照機械臂工作空間求得,并作為衡量機器人運動能力的重要指標.

2.1 仿生蟑螂步行足工作空間求解

蟑螂機器人足端工作空間就是機器人足端在機構限制下所能達到的空間點的集合,決定了機器人所能選擇的立足點范圍.工作空間越大,機器人末端操作空間越大,步行足的靈活性也越大.

應用蒙特卡洛法隨機選取關節空間變量組合,然后根據機器人正向運動學計算出足端坐標,這些坐標值的集合就形成了機器人足端的工作空間[13].

取機器人一條腿為研究對象,根據 D-H法建立坐標系,如圖 4所示,表 1為其 D-H參數.

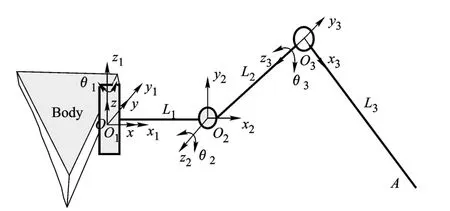
圖4 步行足 D-H坐標系示意圖

表 1 步行足D-H參數表

由機器人前向運動學可知,步行足末端 A在固定坐標系 O-xyz中的坐標為

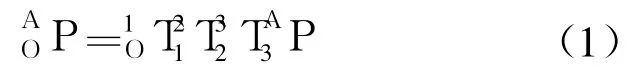
在各個關節變量的變化范圍內,隨機生成 n組關節變量的組合,由式(1)求出其固定坐標值,將 n組點同時顯示出來,就形成了機器人步行足擺動腿的工作空間點云圖.

圖5所示為采用 30 000個隨機點,取 L1=50mm,L2=100mm,L3=200mm時步行足工作空間點云圖及其在 xy平面的投影.

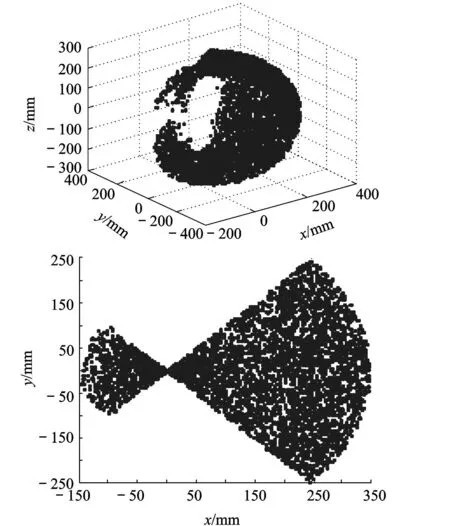
圖5 擺動步行足工作空間及其 xy面投影

2.2 工作空間大小與關節長度的關系

機器蟑螂單腿工作空間的體積大小,直接決定了其躲避障礙和選擇立足點的空間大小.在各個關節轉角范圍一定的情況下,各個關節桿的長度比例是影響工作空間大小的主要因素.因此以工作空間體積大小為目標合理配置關節桿長.

2.2.1 工作空間大小計算

工作空間點云圖顯示了工作空間的形狀,所得到的是一系列離散的數據點.其體積大小則需要根據這些離散點,采用微積分的思想求出[12].

具體步驟如下:1)沿 z向,將工作空間等分為 n塊平面片;2)對每個平面片,沿 x方向再次等分為 m個矩形條,用每個矩形條的面積和來近似實際面積;

3)求和得出每個平面片的面積,與 z向間距相乘后再求和,即可得出工作空間的近似體積.

對于可能存在的空洞,需要進行判斷:將 x方向等分的 m個矩形長條中的 y坐標進行排序,然后判斷相鄰的兩個值是否相差很大,例如若超過等分間距的 3倍,即視為空洞,加以剔除.

2.2.2 工作空間大小與關節長度比例的關系

隨著各個關節桿長度比例的不同,機器人步行足工作空間大小在不斷變化,因此,需要選擇合理的長度比例配置,滿足工作空間最大的原則.

設機器人的單腿長度為 350mm,其中基節比例為 μ1,股節比例為 μ2,脛節則為 1-μ1-μ2.取μ1∈ [0,0.4],μ2∈ [0,0.6],編程計算關節比例和工作空間體積的關系,結果如圖 6所示.

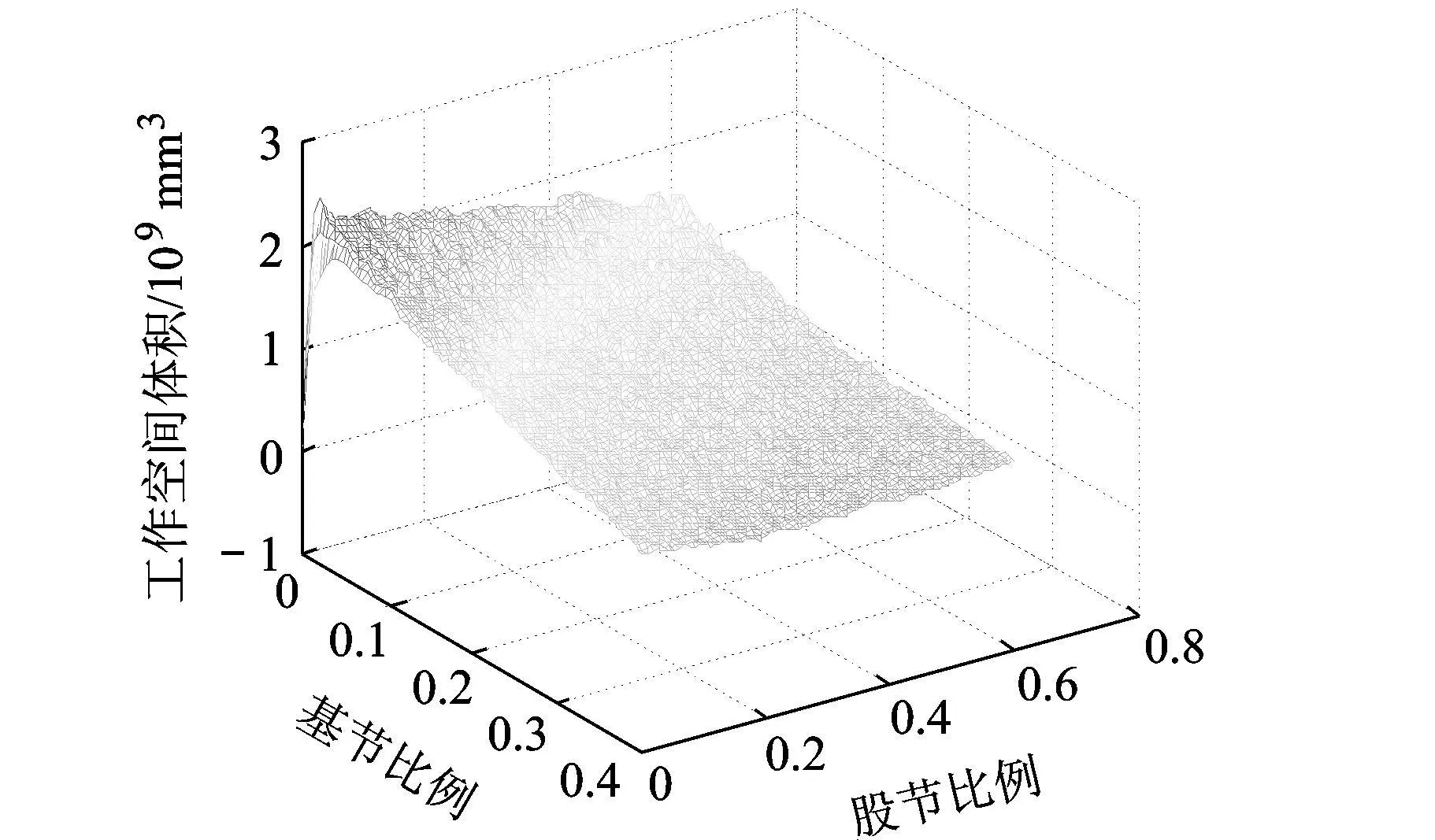
圖6 關節比例與工作空間體積關系

可以看出,基節比例在[0,0.1]之間,股節比例在[0,0.3]之間時,工作空間體積較大,此時單腿的靈活性較高.機器人可以在較大的工作空間內自主選擇立足點,從而可以更加靈活地適應各種復雜的路面情況.

3 基于軀體靈巧度的參數優化

蟑螂機器人處于站立或者采用三角步態行走時,其軀體從機構學角度看,分別是一個由 6條、3條支撐腿組成的復合多變的多支鏈閉環并聯機構.

運動機構應該遠離奇異形位.當機器人接近奇異形位時,其雅克比矩陣為病態矩陣,逆矩陣精度降低,從而使輸入和輸出運動間的傳遞失真.

靈巧度就是衡量這種失真程度的指標,目前對于靈巧性的考察,主要有雅克比矩陣條件數、可操作度等指標.矩陣的條件數定量的表示矩陣求逆的精度和穩定性,因此本文用矩陣條件數來表示機器人的靈巧性.

3.1 仿生蟑螂機體雅克比矩陣

對于仿生蟑螂這樣的多支鏈并聯機構,首先要研究其單腿的雅克比矩陣[14-15],建立相應的坐標系,如圖 7所示.

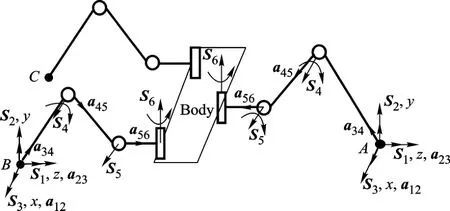
圖7 仿生蟑螂步行足相關坐標系

從機體開始,單腿依次由一個球關節(與地接觸)和 3個轉動關節組成.球關節可以看成圖 8所示的 3個串聯轉動關節的組合.

圖8 球關節簡化為旋轉關節

主運動副軸線用單位矢量Si表示,相鄰軸線間公法線為單位矢量 a12,a23,…,aij,公法線間沿Si的偏距為 Si,公法線長度為 aij,公法線間轉角為 θj,坐標系間轉角為 αij.

機器人單腿分支關節角與仿生蟑螂機體之間的關系見下式:

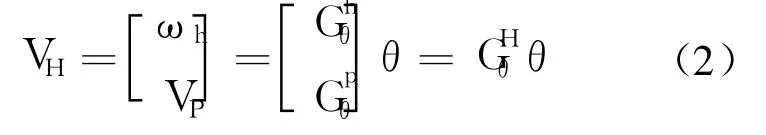
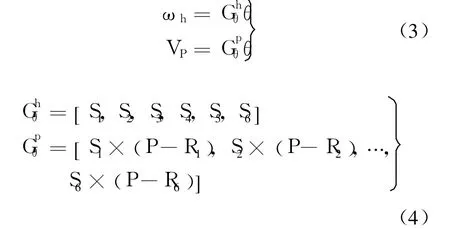
其中

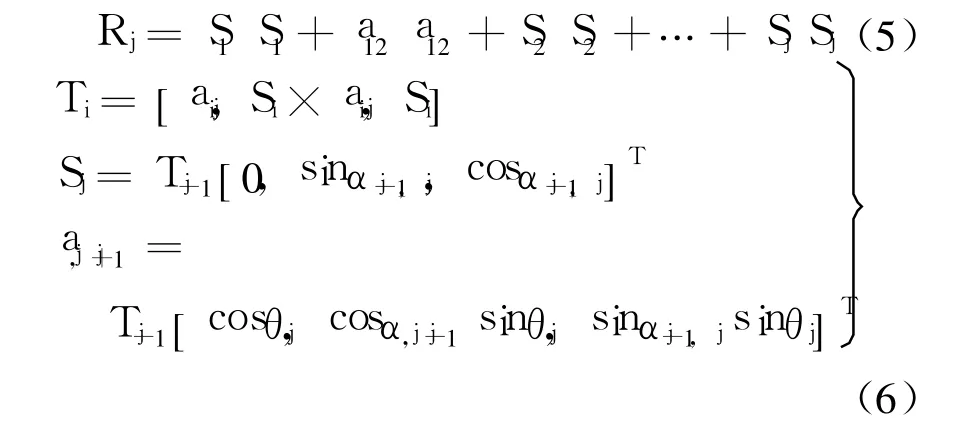
P為機體重心在分支腿末端坐標系中的坐標,根據幾何關系和各個關節桿的長度,向末端坐標系進行投影可以獲得.初始時:S1=[0,0,1]T,a12=[cosθ1,sinθ1,0]T.

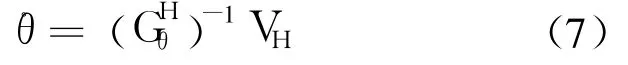
蟑螂機器人通常采用三角步態行走,有三條支撐腿,不妨取 1,3,5腿.在此位姿下,這 3個分支腿與機體的運動關系分別為

蟑螂機器人各分支中只有 4,5,6關節為主動關節,因此,取出上面各矩陣的 4,5,6行組成:

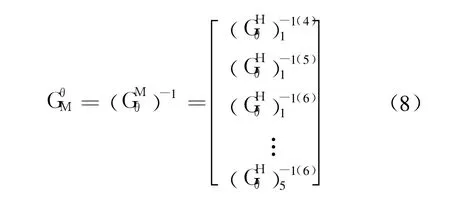
3.2 基于靈巧度的機構參數優化

表 2為采用三足支撐爬行狀態下仿生蟑螂1,3,5腿的相關參數.

表 2 仿生蟑螂支撐腿坐標系相關參數

由式(2)～式(9)可計算出此位姿下機器人的雅克比矩陣.在固定的形位下,雅克比矩陣及其條件數和機器人的機構尺寸關系緊密.因此,以雅克比矩陣的條件數倒數為靈巧度指標優化關節參數.

采用 Frobenius范數計算雅克比矩陣條件數,G表示雅克比矩陣,則靈巧度指標為

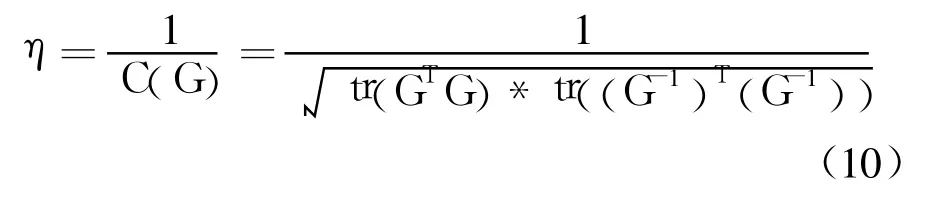
根據不同的關節長度比例配置,以 η∈[0,1]為指標,在 MATLAB中編程計算出關節桿長和靈巧度的關系如圖 9所示.

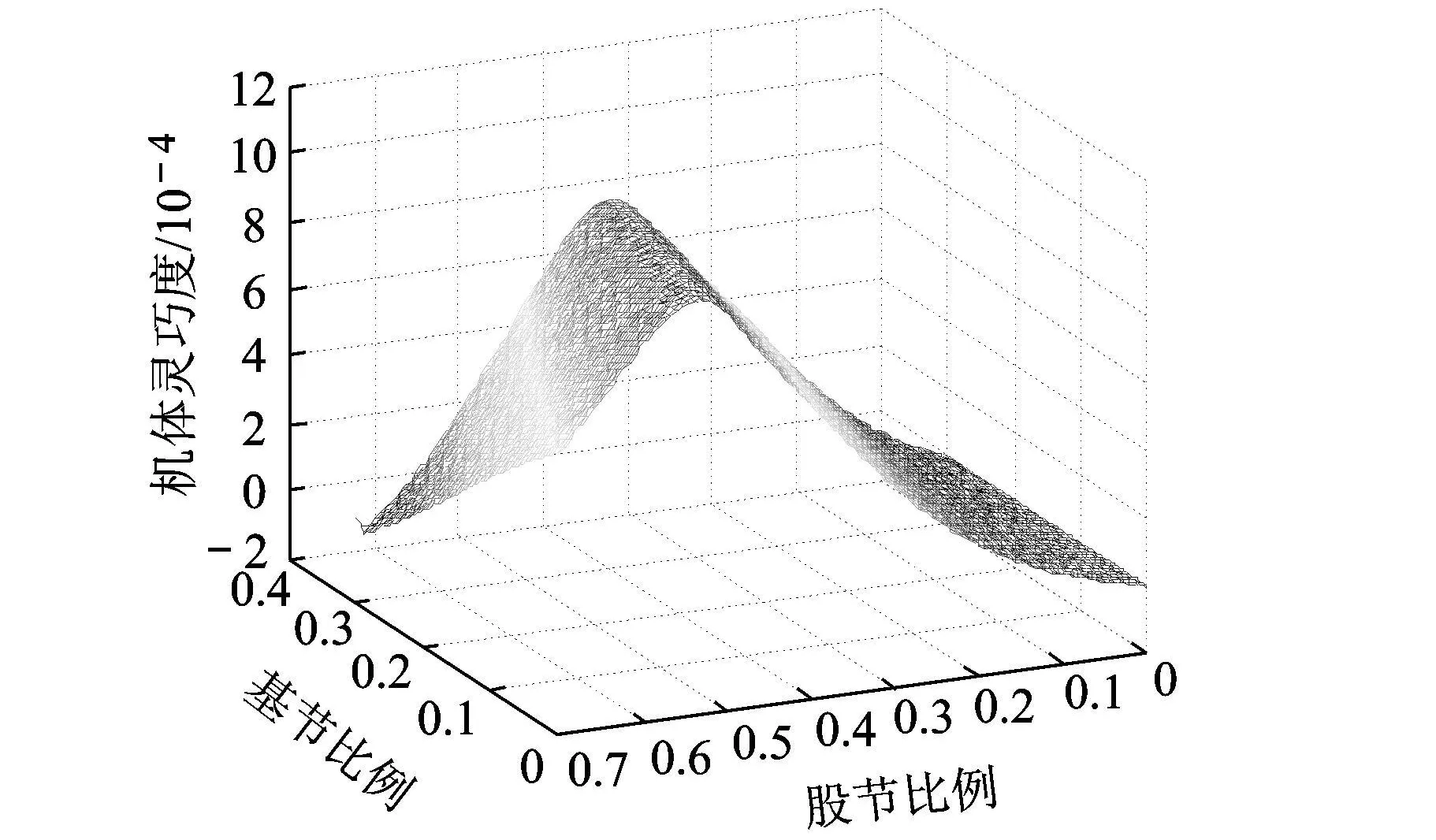
圖9 靈巧度與關節長度比例關系

可以看出,當基節比例在[0,0.1]之間,股節比例在[0.3,0.6]之間時,機器人靈巧度較大,接近奇異形位時,輸入和輸出之間的誤差最小,機器人可以穩定可靠地執行運動命令,整機運動性能較高且靈活可靠.

綜合可知,采用橢圓對稱型身體結構,基節桿長取為單腿總長的 0.05,股節比例取為 0.3,脛節比例為 0.65,蟑螂機器人單腿和整機的運動靈活性和可靠性都比較好,機器人可以在較大的范圍內適應復雜路面情況,靈活選擇合適的立足點,同時能保證較高的運動精度和可靠性.

4 仿真研究

利用 ADAMS參數化建模和評估功能,建立仿生蟑螂機器人的參數化模型,通過試驗設計(DOE,Design Of Experiments)的方法同時研究基節和股節比例變化對機器人整體的影響.

采用文獻[9]提出的評價指標靈活度 F作為試驗設計的評價目標.

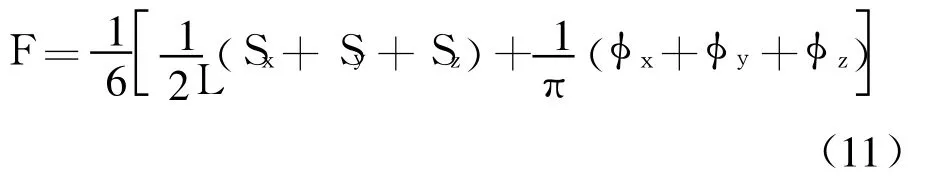
式中,Sx,Sy,Sz和 φx,φy,φz分別表示機器人沿 x,y,z 3個方向所能移動和轉動的最大范圍.

參照文獻[11],利用 ADAMS建立機器人參數化模型,見圖 10.將基節和股節的比例設置為參變量,以 F最大化為目標進行 DOE計算,計算結果圖 11.基節比例范圍取[0.01,0.2],股節比例范圍取[0.3,0.5].

圖10 ADAMS中仿生蟑螂機器人參數化模型

圖11 ADAMS試驗設計結果

可以看出,當基節比例較小時 (圖 11中0.01～0.045),由于容易發生干涉,F較小;當基節比例為 0.045,股節比例為 0.3時,F最大,表明此時機器人機體所能運動的范圍和運動能力最大;之后隨著基節和股節比例的增大,F減小.

仿真結果表明:在不影響整機布置和裝配關系時,取基節比例 0.045,股節比例 0.3時,機器人具有較好的運動能力和靈活性.這與理論分析中所取的基節比例 0.05和股節比例 0.3相一致,從而驗證了理論分析的正確性和可行性.

5 結 論

本文從仿生蟑螂機器人的機構學特點出發,選擇采用橢圓形身體布局,基于運動靈活性分別以單腿的工作空間和整機的雅克比矩陣條件數倒數作為靈巧度目標,對其機構參數進行優化,確定了各個關節桿長的最優配置.并通過 ADASMS仿真模型,進行了試驗設計,結果表明優化后的機器人運動性能良好,運動靈活,與理論分析吻合,驗證了優化配置的可行性和正確性,為其他六足機器人的驅動和控制等進一步研究奠定了基礎.

References)

[1]Bai Shaoping,Low K H,Guo Weimiao.Kinematographic experimentson legmovements and body trajectoriesof cockroach walking on diffent terrain[C]//Proc of IEEE Inter Conf on Robotics and Automation.San Francisco:IEEE,2000:2605-2610

[2]Chen Weihai,Yang Guilin,Ho E H L,et al.Interactive motion controlofmodular reconfigurablemanipulators[C]//Inter Conf on Intelligent Robots and Systems.Las Vegas:IEEE,2003:1620-1625

[3]Gosselin CM,Angeles J.The optimum kinematic design ofa planar 3-DOF parallelmanipulators[J].ASME Journal of Mechanical Design,1998,110(1):35-40

[4]Gosselin C M,Angeles J.A global performance index for the kinematic optimization of robotic manipulators[J].ASME Journal of Mechanical Design,1991,113(3):220-226

[5]Kumar V.Characterization of workspacesofparallelmanipulators[J].ASME Journalof Mechanical Design,1992,114(3):368-375

[6]Xu Qingsong,Li Yangmin.K inematic analysis and optimization of a new compliant parallel Micromanipulator[J].Inter Journal of Advanced Robotic Systems,2006,3(4):351-358

[7]Kircanski M.Kinematic isotropy and optimal kinematic design of planar manipulators and a 3-DOF spatial manipulator[J].International Journal of Robotic Research,1996,15(1):61-77

[8]唐粲,贠超,欒勝.一種新型醫療機器人運動學及靈活性分析[J].北京航空航天大學學報,2005,31(7):748-752 Tang Can,Yun Chao,Luan Sheng.Analysis of kinematics and dexterity for new surgery robot[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(7):748-752(in Chinese)

[9]趙鐵石,趙永生,黃真.仿蟹步行機構模型靈活度分析 [J].中國機械工程,1998,9(3):52-54 Zhao Tieshi,Zhao Yongsheng,Huang Zhen.The flexibility of walking machine imitating a crab[J].China Mechanical Engineering,1998,9(3):52-54(in Chinese)

[10]韓寶玲,王秋麗,羅慶生.六足仿生步行機器人足端工作空間和靈活度研究 [J].機械設計與研究,2006,22(4):10-12 Han Baoling,Wang Qiuli,Luo Qingsheng.Mechanical optimization and analyses of hex apod walking bio-robot[J].Machine Design and Research,2006,22(4):10-12(in Chinese)

[11]羅慶生,韓寶玲.現代仿生機器人設計[M].北京:電子工業出版社,2008:48-60 Luo Qingsheng,Han Baoling.The design ofmodern bionic robot[M].Beijing:Publish House of Electronics Industry,2008:48-60(in Chinese)

[12]曹毅.顯微外科手術機器人工作空間分析與綜合[D].天津:天津大學機械工程學院,2004 Cao Yi.Workspace analysisand synthesis ofmicrosurgical robot[D].Tianjing:School ofMechanical Engineering,TianjingUniversity,2004(in Chinese)

[13]張明.機器人工作空間仿真研究 [J].現代機械,2000(4):38-39 Zhang Ming.The simulation research of robot workspace[J].Modern Machinery,2000(4):38-39(in Chinese)

[14]黃真,孔令富,方躍法.并聯機器人機構學理論及控制[M].北京:機械工業出版社,1997:91-103 Huang Zhen,Kong Lingfu,Fang Yuefa.Theory and control of mechanism for parallel robotics[M].Beijing:China Machine Press,1997:91-108(in Chinese)

[15]孫磊.仿生機器蟹原理樣機的研究[D].哈爾濱:哈爾濱工程大學機電工程學院,2005 Sun Lei.Research on theprototype of crab-like robot[D].Harbin:College of Mechanical and Electrical Engineering,Harbin Engineering University,2005(in Chinese)

(編 輯 :李 晶)

Mechanism optimization of bionic cock roach robot based on locomotion dexterity

Zhang Jianbin Song Ronggui Chen Weihai Zhang Guangping

(School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

The oval body con figuration based on the characteristic of mechanism and the locomotion dexterity ofa bionic cockroach robot was chosen.The workspace of a single leg and the dexterity denoted by the reciprocal of condition number of the whole body's Jacobian matrix were used to optimize and configure the parameters of mechanism.The optimal length ratios of links were decided via dexterity and reliability.The parameterization simulation model was built in ADAMS.Simulation result according with the analysis by theory indicates that the optimization and con figuration are correct and suitable.This method provides a basis for the development of actual pro to and the control of bionic cockroach robot.It also can be referable for the design of other hexapod robots.

bionic cockroach robot;dexterity;optimization;Jacobian matrix

TP 242

A

1001-5965(2010)05-0513-05

2009-06-15

國家 863計劃資助項目(2008AA 04Z210);國家自然科學基金資助項目(60775059);北京市自然科學基金資助項目(3093021)

張建斌(1960-),男,江西萍鄉人,教授,jbzhang@buaa.edu.cn.