乏信息材料布氏硬度測量誤差的灰自助預報

王中宇 葛樂矣 佟 杰 席同鑫

(北京航空航天大學 儀器科學與光電工程學院,北京 100191)

乏信息材料布氏硬度測量誤差的灰自助預報

王中宇 葛樂矣 佟 杰 席同鑫

(北京航空航天大學 儀器科學與光電工程學院,北京 100191)

乏信息材料布氏硬度測量誤差的預報是硬度計量領域的新興課題,有別于傳統的統計學理論,綜合灰色系統理論和自助法的理論知識,提出一種實現乏信息材料布氏硬度測量誤差預報新方法.對小樣本空間的材料布氏硬度測量數據中各誤差源影響進行標定,計算各誤差源對測量結果的誤差傳遞系數,并對各誤差源數據序列進行自助法抽樣,通過灰自助融合建模獲得誤差源標定預測值;按照誤差合成的方法實現乏信息材料布氏硬度測量誤差的灰自助預報.通過具體的實例進行計算,所得的預報結果與采用標準硬度機所得測量結果一致,驗證了乏信息材料布氏硬度測量誤差灰自助預報新方法.

乏信息;測量誤差;灰自助;材料;布氏硬度測量

乏信息(貧信息),是指信息缺乏或嚴重缺失[1].在信息科學與系統科學研究中,乏信息系統被描述為信息不完備的不確定性系統.

誤差是評價硬度測量結果質量的關鍵指標[2],對于實際的材料布氏硬度測量,由于測得值序列的概率分布常常未知或很復雜,同時僅有小樣本的測量數據可供參考和分析[3],因此材料布氏硬度測量的誤差預報屬于乏信息問題.

測量不確定度表示指南(GUM,Guide quantifying Uncertainty analytical Measurement)可以用于材料硬度測量誤差的合成,即按照測量誤差合成法則,分析布氏硬度機測量過程中各誤差源信息,計算得到布氏硬度機材料硬度測量結果的誤差[4].這種基于 GUM的合成計算方法常常需要大樣本的測量數據并且須定量計算誤差源之間的相關關系,而這正是乏信息系統所不具備的條件,而且依據 GUM進行測量誤差分析時并不能對測量誤差進行準確預報.蒙特卡羅方法亦稱統計模擬方法,是以概率統計理論為基礎的利用隨機數進行數值模擬的一種方法[5],國內外已有工程技術人員采用蒙特卡羅方法對布氏硬度機測得的材料硬度的測量誤差進行仿真分析,其條件仍然是具備大樣本量的趨勢先驗測量數據,如文獻[6]中應用蒙特卡羅方法實現了虛擬儀器測量誤差的仿真計算.

對于這種測量數據很少且測量數據總體概率分布很復雜或未知的乏信息誤差的精確預報問題,很難用經典的統計學方法解決,而灰色系統理論、模糊集合理論、粗集理論等新理論新方法,在處理這類問題時顯示出一定的優越性.如文獻[7]中成功將模糊集合理論應用到測量誤差計算過程中;文獻[8]中應用灰色方法實現了小樣本條件下動態測量誤差的精確計算.

本文通過灰自助樣本的抽取擴充了已有數據的樣本空間,彌補了 GUM在乏信息數據處理應用中的局限性,在預報結果上能和實際測量誤差達到較好的一致性,且對于大樣本測量數據,同樣可取得高質量的誤差預報結果.

1 材料硬度測量誤差預報原理

1.1 材料硬度測量原理

對于未經淬火鋼、鑄鐵、有色金屬及質地較軟的軸承合金等材料,可采用布氏硬度機測量硬度,即在一定實驗條件下,在一定實驗力作用下,經規定的實驗力保持時間后卸除實驗力[9-11],以試樣壓痕球形表面積的平均壓力來表示金屬的硬度值,原理如圖 1所示.

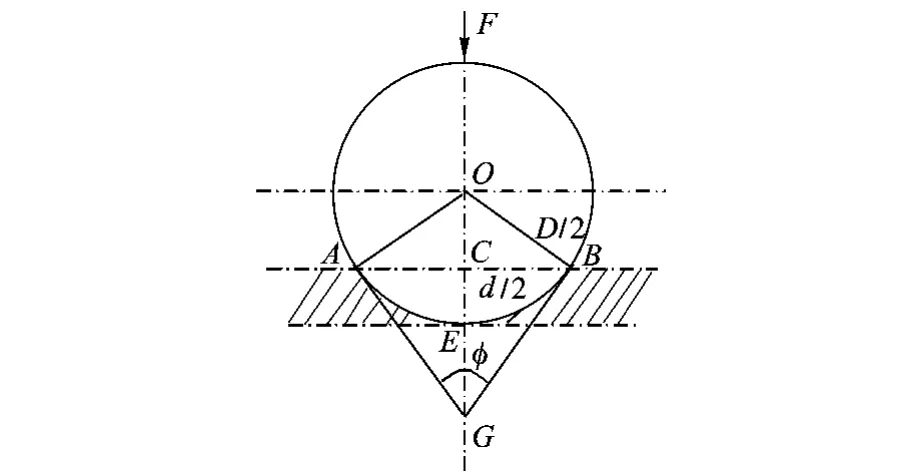
圖1 布氏硬度測量原理

如果以 HB0表示布氏硬度真值,以 HB表示布氏測得值:

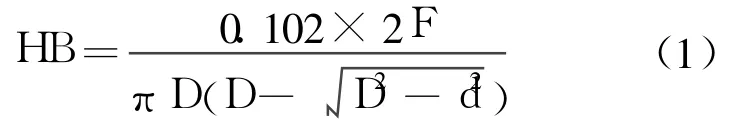
布氏硬度試驗測量結果的誤差為

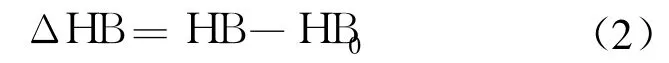
通常使用所有布氏硬度測量結果的平均值作為 HB0的估計值.

1.2 乏信息材料布氏硬度測量誤差預報原理

1.2.1 材料硬度測量誤差源分析

布氏硬度測量誤差分析就是確定各種因素對硬度測量結果的影響.實際硬度測量中,由于各種原因,壓痕直徑測量不可能絕對精確,實驗力、鋼球以及試樣等因素與標準實驗條件也不可能完全一致,因此給布氏硬度測量結果帶來誤差.對測量結果起主要作用的誤差源有 4類[12-15],如表 1所示.

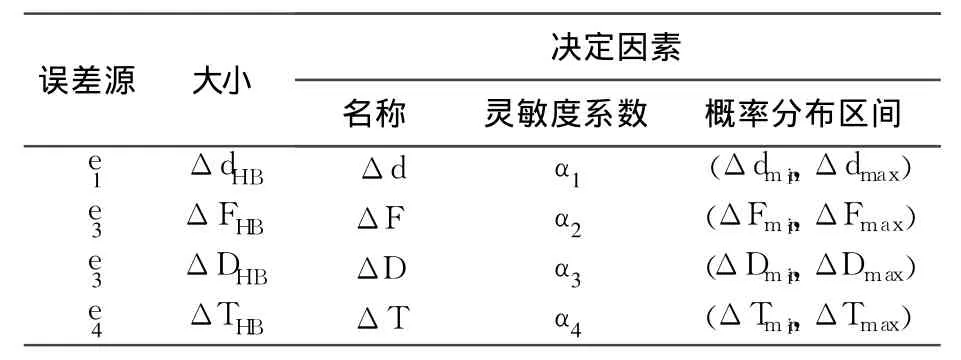
表 1 布氏硬度測量誤差源分析

1.2.2 布氏硬度測量誤差灰自助預報原理

灰自助融合建模(GBFM,Grey Bootstrap Fusion Modeling)是將自助法原理和灰預測 GM(1,1)建模原理有機地結合起來,進行數據分析的一種本征融合方法,又叫灰自助法 GBM(1,1)[16].

布氏硬度測量誤差灰自助預報原理見圖 2.

設小樣本空間的材料硬度測量數據序列的某一種誤差源標定數據為

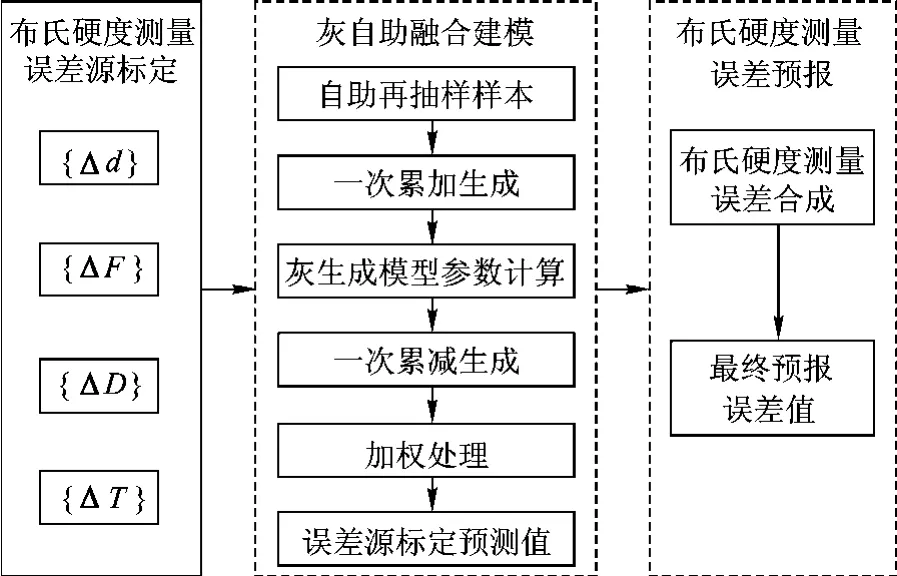
圖2 布氏硬度測量誤差灰自助預報原理

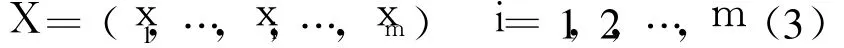
式中,xi為第 i個誤差源標定數據;m為乏信息材料硬度測量數據樣本空間大小;X可以是 Δd,ΔF,ΔD或者 ΔT.

從 X中等概率可放回地隨機抽取 1個數據,抽取 m次,得到第 1個自助樣本,它有 m個數據.連續重復 B次,得到 B個自助再抽樣樣本,用向量表示為

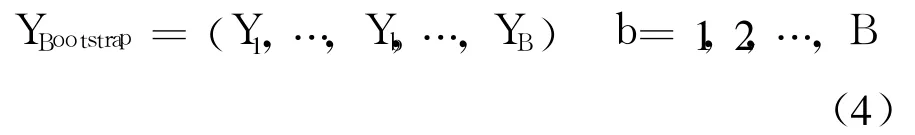
式中,Yb為第 b個自助樣本,且有

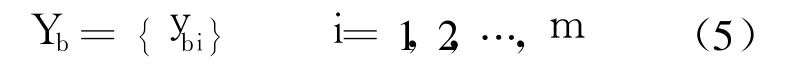
式中,ybi為 Yb中第 i個自助再抽樣數據.

由灰預測 GM(1,1),設 Yb的一次累加生成序列向量為

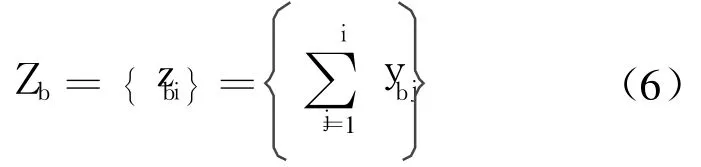
灰生成模型可以描述為如下的灰微分方程

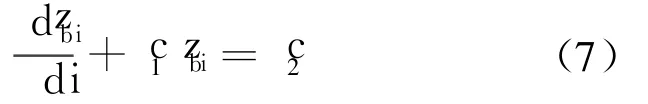
式中,c1和 c2為待定系數,c1≠0.

用增量代替微分,即

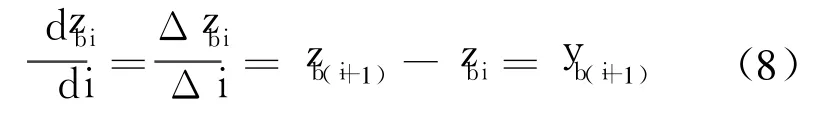
式中,Δi取單位值 1.

設均值生成序列向量為

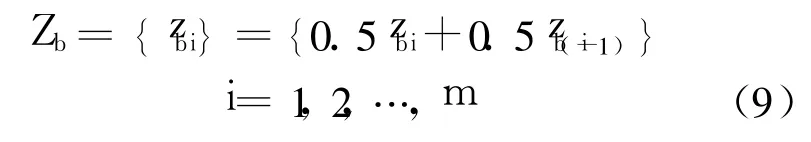
在初始條件 zb1=yb1下,設灰微分方程的最小二乘解為

由累減生成,測量次數 w=i+1的預測值可以表示為

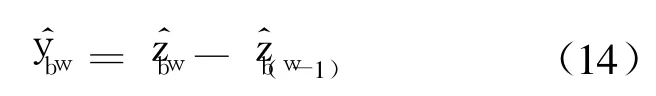
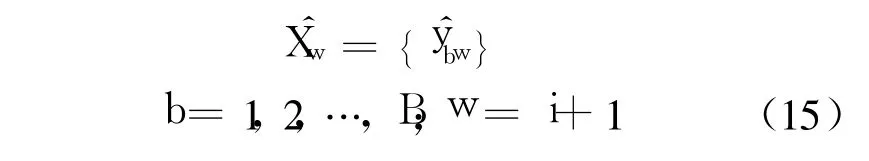
在測量次數 w,有 B個數據,可以構成如下序列向量,即

在測量次數 w的估計真值,即最終解用加權均值表示為

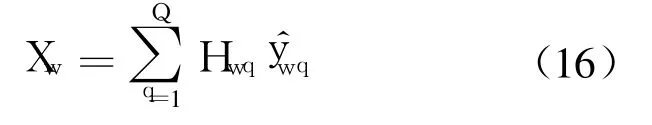
式中,Xw為基于灰自助法的誤差源標定預報值;為第 q組的預測值中值;Hwq為對應于的頻率函數.

根據測量誤差合成公式

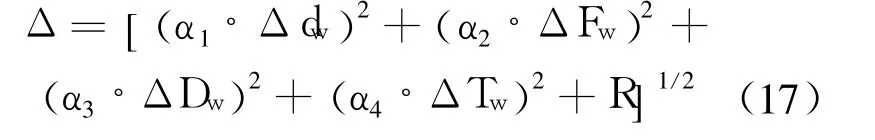
式中

其中,R為各個誤差源之間的協方差;n為梅涅耳指數[17-20].

經過大量的實驗分析,上述 4種誤差之間的相關系數很小,可做不相關處理,因此各個誤差源之間的協方差 R可近似為 0.

2 實例分析

用布氏硬度試驗機對一鋼制試樣進行硬度測量,布氏硬度測量試驗力為 F=29421N,壓頭使用不銹鋼 0Cr18Ni9,鋼球壓頭直徑為 10mm,鋼球球體公差要求為 ±0.005mm,用最小刻度為0.01mm的讀數顯微鏡進行壓痕直徑測量,壓入角 φ=136°,取梅涅耳指數 n=2.1.壓痕直徑誤差和鋼球直徑誤差的標定數據如圖 3所示.

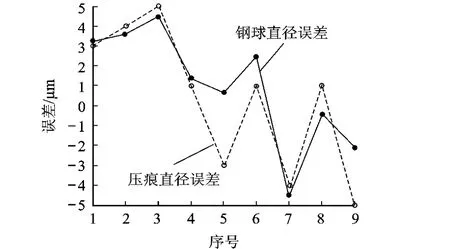
圖3 壓痕直徑誤差和鋼球直徑誤差的標定數據

小樣本布氏硬度測量結果、試驗力誤差標定數據和試樣溫度測量誤差標定數據如表 2所示.

表 2 布氏硬度測量誤差源分析

經計算,得到:

依據 1.2節布氏硬度測量誤差灰自助預報原理,即可得到硬度測量誤差預報值.

本實例分別采用 7組的誤差源標定數據(第1組使用第 1和第 2個實際誤差源標定數組和,第 1和第 2個硬度測得值;第 2組使用第 1、第 2和第 3個實際誤差源標定數組和,第 1、第 2和第3個硬度測得值;其他組依此類推)對硬度測量誤差進行預報,并將結果分別與第 4,5,6,7,8,9個實際測量誤差進行比較,如圖 4所示.

比較結果表明:在乏信息材料布氏硬度測量條件下,按照本文的方法可以很好地實現硬度測量誤差的精確預報,并且隨著灰自助原始樣本的增加,誤差預報值能愈接近于真實的測量誤差值.

3 結 論

鑒于材料布氏硬度測量的原理和特點,本文在灰色系統理論和自助法的基礎上,首創了布氏硬度測量誤差灰自助預報模型,克服了傳統誤差預報方法的一些局限性,在實際的測量中得到了有效驗證.

本文所建立的布氏硬度測量誤差灰自助預報模型能不斷利用有限的測量數據對未來測量誤差進行預測,時刻跟蹤測量誤差的變化,并可實現對測量誤差的實時控制,為布氏硬度測量的誤差溯源和誤差修正奠定基礎.

References)

[1]Gao Y,Wang Z,Tao Z.Estimation of non-statistical uncertainty in precision measurement using grey system theory[J].The International Journal of Advanced Manufacturing Technology,2003,22(3):271-277

[2]ISO/TR 10108 Steel-conversion of hardness values to tensile strength values[S]

[3]Janosec M,Schindler I,Vodarek V,et al.Micro structure and mechanical properties of cold rolled,annealed HSLA strip steels[J].Arch and Civil Mechanical Engineering,2007,7(2):29-38

[4]ISO.Guide to the expression of uncertainty in measurement[S],1993

[5]Wang Zhongyu,Ge Leyi.Novel method of evaluating dynamic repeated measurement uncertainty[J].Journal of Testing and Evaluation,2008,36(5):453-459

[6]Nuccio S,Spataro C.Approaches to evaluate the virtual instrumentation measurement Uncertainties[C]//IMTC.Budapest:IEEE,2001:84-89

[7]Xia Xintao,Wang Zhongyu,Gao Yongsheng.Estimation of nonstatistical uncertainty using fuzzy-set theory[J].Measurement Science and Technology,2000,11(4):430-435

[8]Ge Leyi,Wang Zhongyu.Novel uncertainty-evaluation method of virtual instrument small sample size[J].Journal of Testing and Evaluation,2008,36(3):273-279

[9]GB/T 1172-1999 Black steel hardness and tensile strength[S]

[10]Tien T L.The indirect measurement of tensile strength for a higher temperature by the new model IGDMC(1,n)[J].Measurement,2008,41(6):662-675

[11]Herrmanzinn K,Polzin T.New guidelines to the determination of the uncertainty of hardness measurements[J].Tm-Technisches Messen,2005,72(5):325-333

[12]Roberts SM,Kusiak J,Withers P J,et al.Numerical prediction of the development of particlestress in the forging of alum inium metal matrix composites[J].Journal of Material Proceeding Technology,1996,60(4):711-718

[13]Sonmez F O,Demir A.Analytical relations between hardness and strain for cold formed parts[J].Journal of Material Proceeding Technology,2007,186(3):163-173

[14]Rosenberger M R,Forlerer E,Schvezov C E.Modeling the micro-indentation ofmetalmatrix composites[J].Material Science Engineering:A,2007,463(2):275-283

[15]Burcher M R,Noble JA,Han Lianghao.A system for simultaneously measuring contact force,ultrasound,and position information for use in force-based correction of freehand scanning[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2005,52(8):1330-1342

[16]王中宇.非統計原理及其工程應用[M].北京:科學出版社,2005 Wang Zhongyu.Non-statistical theory and its engineering application[M].Beijing:Scinece Press,2005(in Chinese)

[17]Otero J,Saiz A,Brufau J,et al.Reduced dimensions autonomous AFM system for working in m icrobiorobotics[C]//IEEE/RASEMBS,2006:1200-1205

[18]Hu Tie,Desai J P.Soft-tissue material properties under large deformation:strain rate effect[C]//The 26thAIC/EMBS.San Francisco:IEEE,2004:2758-2761

[19]Albrecht H J,Juritza A,Muller K,et al.Interface reactions in microelectronic solder joints and associated inter metallic compounds:an investigation of their mechanical properties using nanoindentation[C]//The 5thConference on EPT.Singapore:IEEE,2003:726-731

[20]Deng Julong.Introduction to greyness system theory[J].The Journal of Grey System,1989,1(1):1-24

(編 輯:趙海容)

Error predicting for material Brinell hardness measurement of poor information based on grey bootstrap method

Wang Zhongyu Ge Leyi Tong Jie Xi Tongxin

(School of Instrument Science and Opto-electronics Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Error predicting for material Brinell hardness measurement of poor information is a common problem in the field of hardness measurement.Only small sample measurement data obtained for Brinell hardness measurements are destructive.Different from statistical methods,a novel poor information Brinell hardness measure menterrorpre diction method was presented,which was based on grey system theory and bootstrap theory.After calibrated all measurement error sources,all measure ment error transfer coefficients should be calculated and the calibration data of error sources should be sampled in terms of bootstrap theory.The predictions of calibration data of all error sources were gained by a grey Bootsrap fusion model.The error prediction values were obtained for material Brinell hardness measurement of poor information in terms of error combination principle.In an example of a general Brinell hardness measurement,the predicting Brinell hardness measure menterrorsacquired by this novel proposed method and the actual measurement errors were shown to be in a good agreement with each other,and the validity of the proposed method was also represented.

poor information;measurement errors;grey bootstrap;materials;Brinell hardness testing

TH 8

A

1001-5965(2010)05-0524-05

2009-04-13

國家自然科學基金資助項目(50675011);北航博士生創新基金資助項目

王中宇(1963-),男,河南洛陽人,教授,mewan@buaa.edu.cn.