一種基于SVM的航路規劃研究

程春華，吳進華，周大旺

（海軍航空工程學院 a.研究生管理大隊；b.控制工程系，山東 煙臺 264001)

0 引言

航跡規劃定義為在特定約束條件（包括環境約束和運動體自身約束）下，尋找運動物體從起始點到目標點，滿足某種性能指標和某些約束的最優運動路線、路徑[1-2]。對于反艦導彈，其航跡規劃的目的就是通過規劃對島嶼、陸地、警戒雷達區域或其他需要規避的區域進行規避，以達到避開島嶼攻擊目標的作戰目的。假設反艦導彈在遂行任務過程中保持高度不變、速度不變，而且考慮敵方防御區處于平坦地域，那么反艦導彈就無法利用地形因素進行威脅規避機動，航路規劃問題就可以被簡化成為一個二維航路（也就是水平航路）規劃問題。很多學者通過對規劃空間進行網格劃分形成連接起始點和目標點的網絡圖[1-3]，然后采用搜索算法進行航路尋優。許多學者在這方面做了大量的工作，采用了許多智能搜索算法，如A*算法[4]、遺傳算法[5]、蟻群算法[6]、粒子群算法[7]等。JunMiura在文獻[8]中提出了基于SVM的新航路規劃方法，基于此，本文提出了SVM在反艦導彈中的應用，同時本方法也適用于其他飛行器。

1 SVM 概述

支持向量機（SVM）是統計學習理論中最年輕的內容，它包括支持向量分類機（SVC）和支持向量回歸機（SVR）。其中SVC是基于間隔最大化思想尋找最優超平面的分類方法[9-10]。

給定一組線性可分樣本數據集

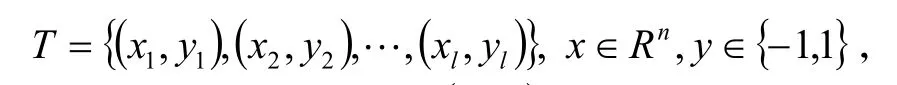
存在惟一的規范超平面(ω?x) +b=0，使得下式成立：

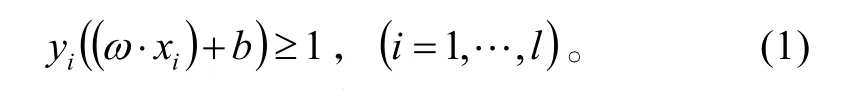
這樣通過超平面就使兩類樣本點落到平面H1:(ω?xi) +b=1和 H2:(ω?xi) +b=?1的兩側（或H1與H2上）。

而平面H1與平面H2之間的距離為它表示了兩類點被分開的程度。SVC就是要在式(1)條件下最大化ρ。求解該問題可以通過求解它的Wolfe對偶問題，即求解下面的二次規劃問題：

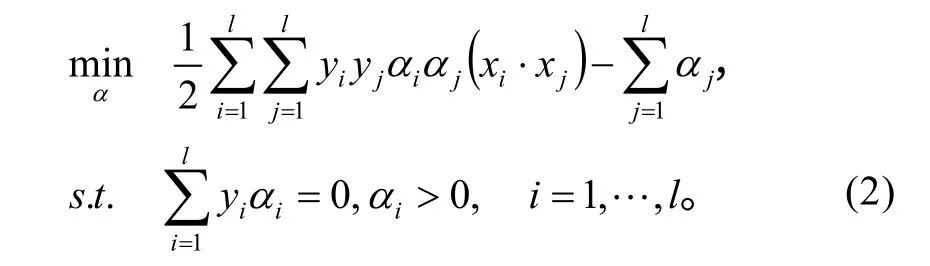
其中與樣本點 xi對應的αi滿足 αi≠0，則 xi叫支持向量，它在平面H1或H2上，是決定平面的向量。求得 α *后就得到了決策函數 f (x)：

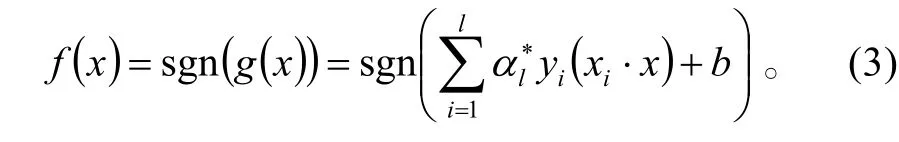
上面是在線性可分的情況下得到的，而很多情況下將是線性不可分劃。對于某些線性不可分問題，線性分劃造成的錯分點可能比較少，這類問題稱為近似線性可分。此時我們使用軟間隔的辦法引入松弛變量iξ 來“軟化”約束條件(1)，

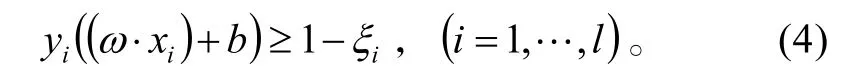
同時在目標函數中引入懲罰參數C，得到如下對偶規劃問題：

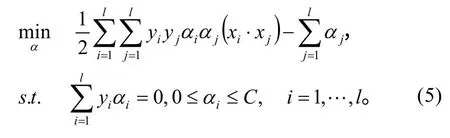
求解結果非零 αi對應了兩類支持向量，一是在平面H1和H2上的普通支持向量，此時 0＜αi＜C；另一種為兩平面間的邊界支持向量，此時 αi=C。

當訓練集T的兩類樣本點集非線性可分時，SVC 通過引進從輸入空間X 到另一個高維的Hilbert 空間H的變換 x ??(x)，將原輸入空間X的訓練集轉化為Hilbert 空間H的新的訓練集：使其在Hilbert 空間H 中線性可分。然后在空間H 中求得超平面(ω??(x))+ b=0，這個超平面可以硬線性分劃訓練集。采用核函數K 滿足

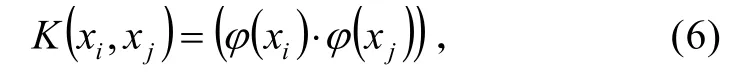
可以避免在高維特征空間進行的復雜運算，解決了“維數災難”。得到的決策函數為

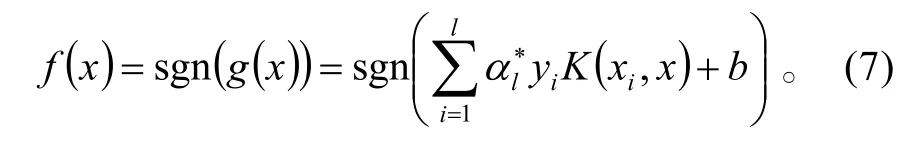
2 SVM 在航跡規劃中的研究

引言中已經將反艦導彈的航跡規劃問題簡化成二維平面的障礙規避問題。此時，航路可以看成障礙中的安全走廊，這條安全走廊將障礙物分成了兩部分：一部分在航路的左邊；另一部分在航路的右方。因此，我們可以利用SVM 良好的分類能力，將這兩部分障礙分開，從而得到分界曲線作為航路。可以看出，要將SVM 應用到航路規劃中來，首先，得對規劃空間進行劃分，將規劃空間中的障礙規劃成兩類[3]；然后，應用SVM的分類能力。本文直接以初始點與目標點的連線為基準線[8]。

2.1 障礙物的劃分

假設(x0,y0)為出發點，(xT,yT)為目標點，則基準線方程為：

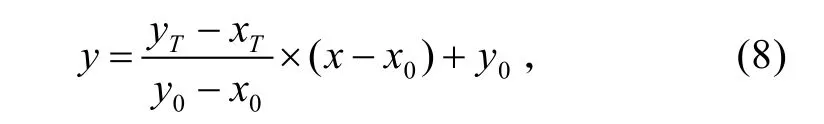
式中：(x,y)為障礙的中心坐標。

根據y的值，規劃空間中所有的障礙可以分成以下兩類：

正類障礙：y＞0；

負類障礙：y＜0。

若y=0，則根據具體的情況來分析：將它分成正類和負類各一次進行規劃，若判別為正類時規劃出的航路短，則為正類，反之亦然。在航路規劃中，先將不互相覆蓋的威脅區域分離開，取它的周圍特征點來表示該威脅區域。如果兩個障礙區域有重疊現象，則可以將它們看成是一個障礙區域。如圖1中，障礙a 和b 重疊，故視為一個障礙。

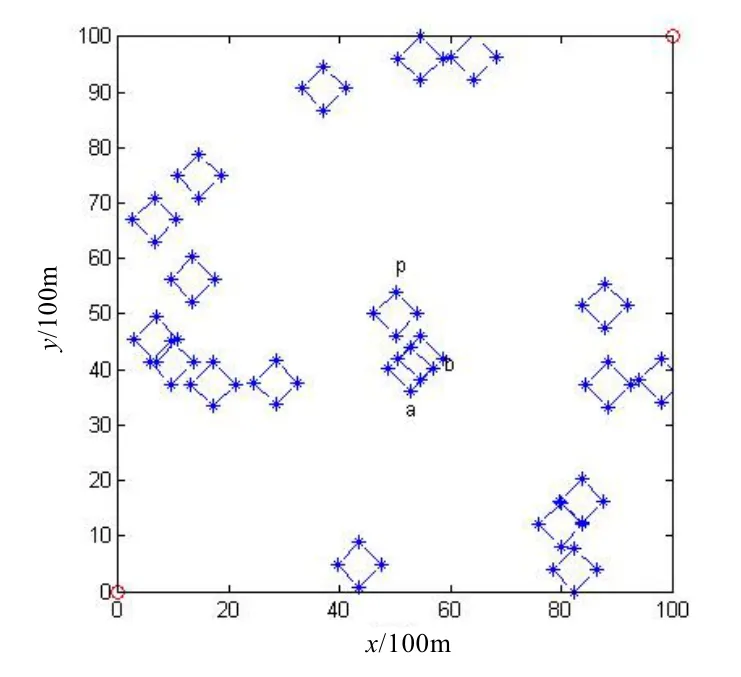
圖1 障礙圖

2.2 SVM 規劃出的航路

利用SVM 對上面的兩類障礙物進行規劃，得出判別決策函數式(7)。取

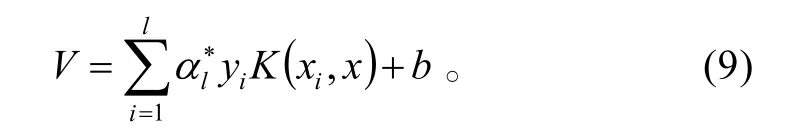
正類障礙區域：V≥1；

負類障礙區域：V≤?1；

安全航路區域（間隔區域）：?1＜V＜1。

我們希望目標點和初始點都落在間隔區域中，這樣就可以尋找從出發點到目的點的航路，同時也確保了反艦彈最安全地飛行[8]。

2.3 輔助障礙點的選取

我們知道SVM 規劃出的間隔區域有可能是非連通的。為了盡量使出發點和目標點落在同一間隔區域內，我們加入了一些輔助障礙點引導間隔區域經過出發點和目標點。

輔助障礙點的選取：

1）在出發點和目標點附近

為了確保間隔區域經過出發點和目標點，我們在它們兩側分別設了N個正類、負類障礙點，并且平行于標準線，如圖2所示。

圖2 障礙點和輔助點圖

2）中間輔助障礙點的選取

輔助障礙點的選取可以引導SVM 作出我們所需要的間隔區域。但是它畢竟是虛設的，所以不能影響實際存在的障礙。所以要以一定的距離平行標準線選取，本文取各類障礙距離標準線的平均距離dE，則兩類輔助障礙點的方程為：

3 仿真驗證

在仿真過程中，選取規劃的區域是1×100km2正方形區域，設置了20個邊長為400×m的正方形障礙，其中正方形障礙P是特別設定的，正好位于出發點和目標點的連線上。其他的是隨機生成的障礙。在仿真過程中我們采用了高斯徑向基函數

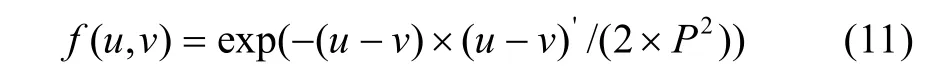
作為SVM的核函數，其中P 選為10，C 選為300。仿真結果如圖3所示。

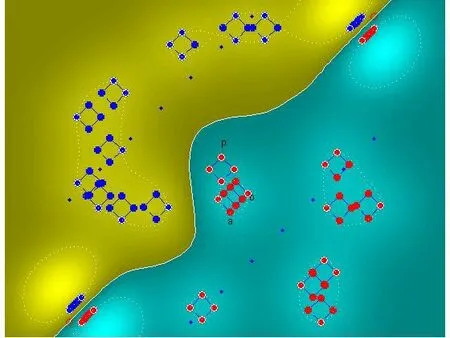
圖3 基于SVM的障礙分類圖

從而得到實際飛行航跡圖如圖4所示，此時SVM的支撐向量的個數為50個，占全部向量的41.7%。當P 選為25，C 選為300，此時仿真結果如圖5所示，此時SVM的支撐向量的個數為20個，占全部向量的16.7%。

圖4 實際飛行航跡圖

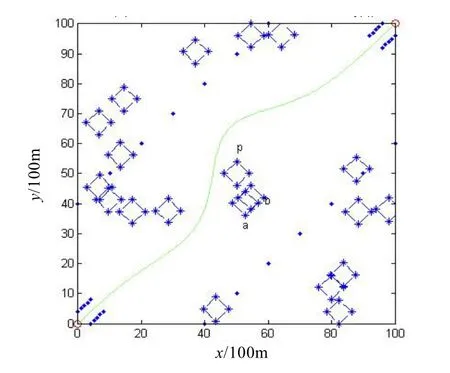
圖5 實際飛行航跡圖

由圖5可以看出SVM 用于航跡規劃是可行的，雖然該方法不能保證航跡最短，但是在燃料條件等允許的條件下，它能保證飛行器最安全地在障礙間飛行，并且由SVM 規劃出的航跡還不必進行光順處理。同時，也存在缺陷，就是有關核函數及其參數的選取對結果影響很大。

4 結論及展望

本文研究了SVM 在航路規劃中的應用，從仿真結果來看，它是一種有效可行的方法，由它規劃出的航跡不必進行光順處理。但同時，核函數及其參數的選取一直是SVM 問題中的難題，也將成為SVM 在航跡規劃中應用的瓶頸。再者，本文僅研究了無威脅的障礙，對于其威脅性是有待進一步研究的問題。

[1]柳長安,李為吉,王和平.基于蟻群算法的無人機航路規劃[J].空軍工程大學學報:自然科學版,2004,5(2):9-12.

[2]葉文,朱愛紅,范洪達.低空突防航路規劃算法綜述[J].系統仿真學報,2007,19(10):2357-2361.

[3]張雅妮,高金源.一種基于改進A*算法的三維航跡規劃方法[J].飛行力學,2008,26(1):48-51.

[4]范晨,王正杰.基于A*算法的飛行器三維航跡規劃研究[J].彈箭與制導學報,2006,26(1):650-656.

[5]虞蕾,趙紅,趙宗濤.一種基于遺傳算法的航跡優化方法[J].西北大學學報:自然科學版,2006,36(2):205-213.

[6]李棟,曹義華,蘇媛,等.基于改進蟻群算法的低空突防航跡規劃[J].北京航空航天大學學報,2006,32(3):258-262.

[7]陳冬,周德云,馮琦.基于粒子群優化算法的無人機航跡規劃[J].彈箭與制導學報,2007,27(4):340-342.

[8]JUN MIURA.Support Vector Path Planning[C]//Proceedings of the 2006 IEEE/RSJ.International Conference on Intelligent Robots and Systems,BJ:IEEE Press,2006:2894-2899.

[9]鄧乃揚,田英杰.數據挖掘中的新方法——支持向量機[M].北京:科學出版社,2004.

[10]VAPNIK V N.Statistical Learning Theory[M].John Wiley &Sons,New York,1998.