一種多分量chirp信號陣列檢測新方法

（海軍航空工程學院 電子信息工程系，山東 煙臺 264001）

Chirp類信號是信號處理領域的常見信號之一，不管是在自然界的天然信號中，還是人為產生的信號中，都大量存在。因此，多分量chirp信號的檢測和參數估計一直受到人們的關注。近年來隨著分數階傅里葉變換理論的迅速發展而產生了多種基于分數階傅里葉變換的多分量chirp信號檢測和參數估計算法[1-7]。該類方法能夠有效實現chirp信號的同時四參數估計，性能分析和仿真結果都證明其檢測效果和估計精度均優于原有時頻類算法。不過，該類算法的現有研究成果均針對的是單陣元信號，而隨著天線技術的發展，目前雷達、通信等許多系統中都采用了陣列天線來提高系統性能。因此，本文研究了如何利用陣列信號處理技術來提高現有算法[1]的檢測和參數估計性能。

1 預備知識

1.1 信號模型

本文所用模型如下：

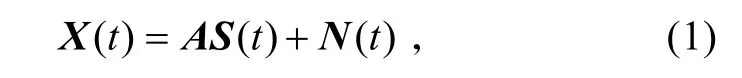
式中：S (t)=[s1(t),…,sN(t)]T為N個源信號構成的N維向量；X(t)=[x1(t),…,xM(t)]T為M 維觀測數據向量，其元素是M個傳感單元的輸出信號；M×N (M≥N)維矩陣 A=[a1,…,aN]稱為混合矩陣，其元素表示信號的混合情況，列向量 ai=[ai1,…,aiM]T代表第i個信源的空間特性；是M×1 維噪聲向量。

式(1)的含義是N個源信號 S (t)通過空間特性為A的陣列后得到M 維觀測數據向量 X (t)。為簡化討論，假定=M，這個假設并不會影響下面的討論結果。

1.2 基于分數階傅里葉變換的Chirp信號參數估計

多分量chirp信號可用以下模型表示：

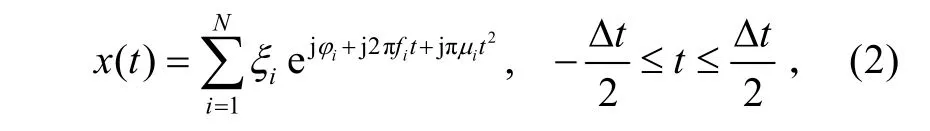
式中：iξ為幅度；fi為中心頻率；iμ為調頻率；i?為初相。

分數階傅里葉變換（FRFT）定義可參看文獻[8]。利用分數階傅里葉變換與時頻分布的關系，可實現chirp信號的檢測與參數估計[1]：

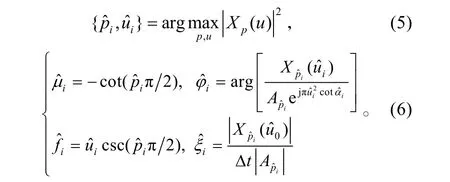
上述方法可以推廣到多分量chirp信號的檢測與參數估計，當多分量信號之間強度相差較大時，可采用從強到弱逐個消去的方法來抑制強分量對弱分量的影響[1]。但前提條件是多分量chirp信號之間的強度相差較大，弱分量對強分量的干擾很小，而能夠較為準確地依次消去強分量。但是，在實際應用中上述條件往往難以保證，尤其是當信號分量較多，各分量之間的強度相差不大，且參數相近時，式(5)的取模運算會導致各分量間的相互影響增強，此時多分量之間的相互干擾會大大降低檢測和參數估計的性能[9]。

為了解決這個問題，本文利用天線陣列通過分數階傅里葉域陣列加權來抑制噪聲和干擾項的影響，從而有效提高原有方法的性能。

2 分數階傅里葉域陣列加權

因為噪聲也可以看作是某個我們并不感興趣的源信號，也就是說，式(1)中的X(t)可以看成為N+1個源信號通過混合矩陣A的產物。那么從分析多分量信號間的相互干擾這個角度出發（將噪聲也作為源信號進行分析），可以將式(1)簡化表示為：

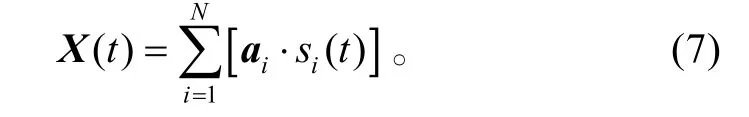
式(7)中為了表達式的簡潔，求和符號的上標仍然用N表示。那么第k個傳感器的輸出為：

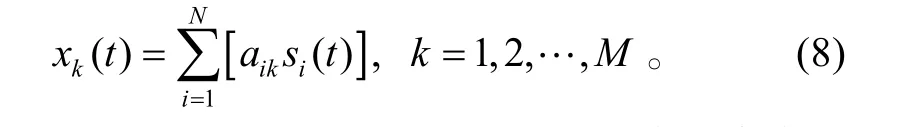
由于FRFT是線性變換，那么對于單個傳感器輸出xk有：

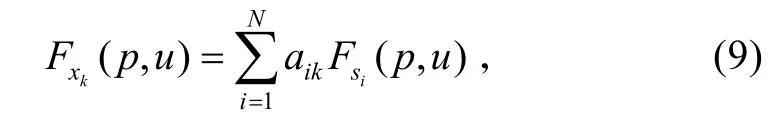
則

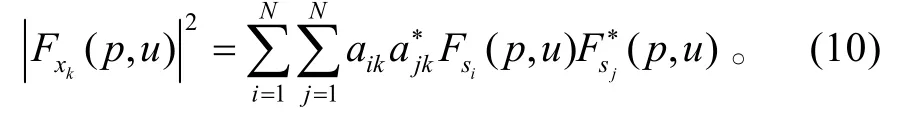
對天線陣各單元輸出信號進行平均后可得：

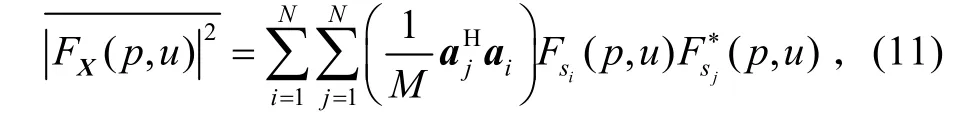
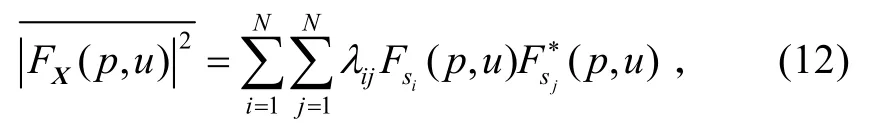
式中：

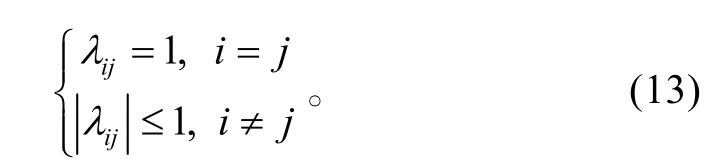
上式表明，天線陣各單元輸出信號進行平均后的FRFT模平方是每個源信號的FRFT模平方和不同源信號之間FRFT 干擾項的線性組合。

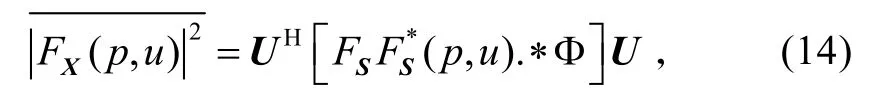
式中：“.?”表示矩陣中對應元素的相乘；U是N×1維的單位向量；

矩陣 FSFS*(p,u).?Φ中，對角元素代表的是每個源信號的FRFT模平方，非對角元素是第i個源信號的FRFT 和第j個源信號FRFT 共軛的乘積，即干擾項。

該矩陣每個元素前也都有一個加權系數 λij，當i=j時，λij=1；當i≠j時，

也就是說，矩陣中對角元素的加權系數均為1，非對角元素其加權系數的模均小于1。這樣，通過對天線陣各單元輸出信號進行平均便能夠很好地抑制不同源信號之間的相互干擾。

3 算法

根據前述內容，可以得到新的檢測和參數估計算法步驟為：

第一步，對每個傳感單元的輸出信號求取其FRFT模平方；

第二步，對第一步所得到的各陣元結果進行求和平均，通過陣列平均來抑制干擾項和噪聲；

第三步，根據式(5)、(6)，在(p,u)平面內對所得到的FRFT模平方平均值進行兩級二維搜索，由峰值點位置得到最強信號分量（i=1）的參數估計值

第四步，利用參數估計值恢復出第一個信號分量為：

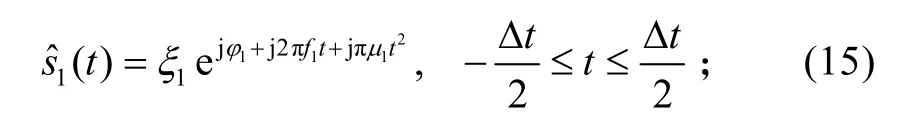
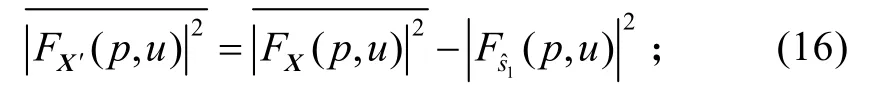
第六步，將第五步結果代入第三步，重復進行上述步驟，依次得到其余的信號分量估計值，直至剩余的FRFT模平方平均值的峰值不再超過預定閾值。

4 仿真

本文仿真中采樣頻率為1 000 Hz，采樣點數為1 000，陣元個數分別取1、4、8。所用兩個chirp信號分別為：

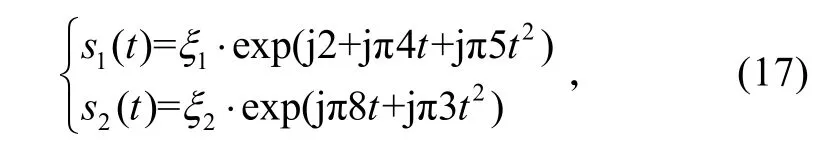
其空間到達方向分別為π/8 和5π/12。

不妨設 s1(t)為有用信號，s2(t)為干擾信號，則干信比ISR=20lg (ξ2ξ1)，變化范圍?16 dB～0 dB。

圖1給出了陣元數分別是1、4、8的參數估計誤差平方隨干信比的變化曲線。從曲線上可以看出，干擾很弱時單陣元和多陣元平均的性能接近。但是，隨著干擾強度的增大，單陣元的估計誤差迅速增大，而多陣元平均的估計誤差雖增長但緩慢得多，并且，陣元個數越多，估計精度越高。

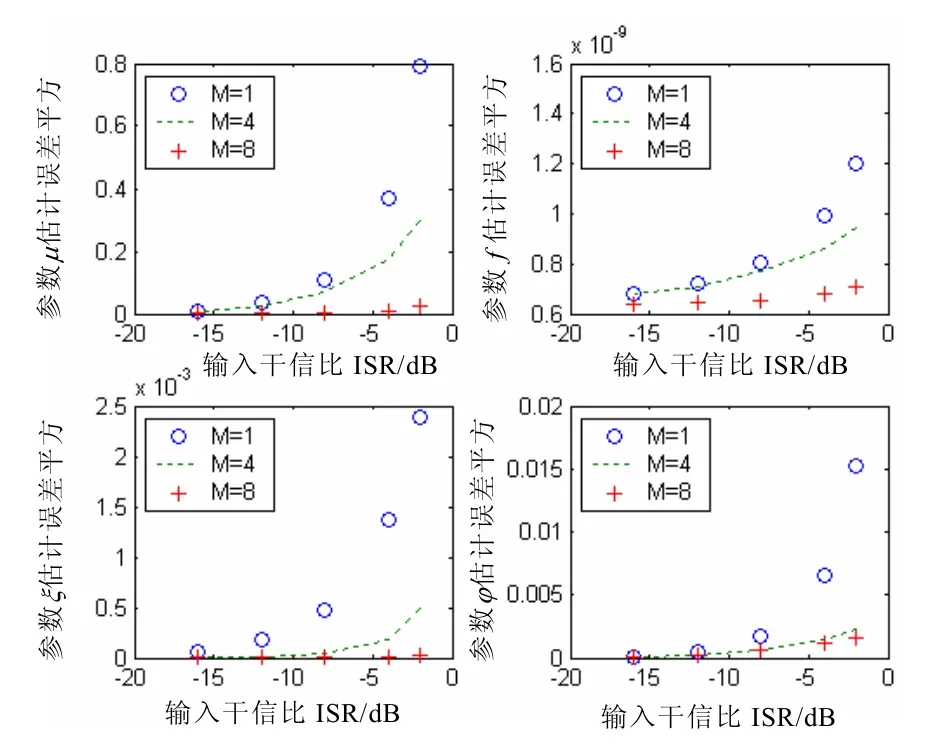
圖1 多參數的估計誤差曲線

接下來進一步定量說明所提算法的有效性，仿真中采用8 陣元均勻線陣，采樣頻率為100 Hz，采樣點數為100，所用信號為s (t)=s1(t)+s2(t)+s3(t)，其中：

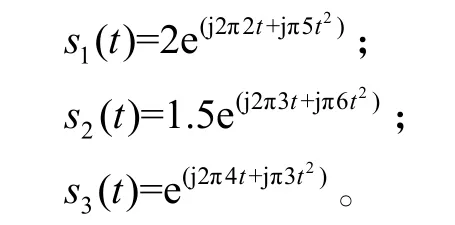
當只用一個陣元來對 s1(t)進行參數估計時，誤差分別為：

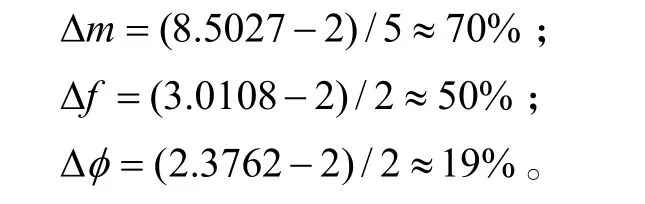
?m、?f、?φ分別表示調頻率、初始頻率和幅度的估計誤差。當采用本文所提方法時，誤差分別是：

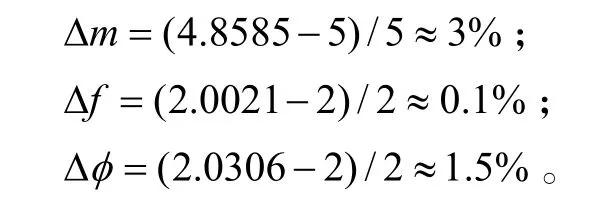
從仿真結果可以看出，本文方法有效地抑制了多信源間的相互干擾。

5 結論

本文提出了一種基于分數階傅里葉域陣列加權的多分量chirp信號檢測和參數估計新方法。仿真結果證明了該方法的有效性和實用性。和單陣元檢測方法相比，新方法大大提高了檢測和參數估計的性能，尤其適用于信噪比較低、信號分量個數較多、各分量強度相差不大且參數相近的情況。

[1]QI LIN,TAO RAN,ZHOU SIYONG,et al.Detection and paramter estimation of multicomponent LFM signal based on the fractional Fourier transform[J].Science in China:Ser.F,Information Science,2004,47(2):184-198.

[2]董永強,陶然,周思永,等.含未知參數的多分量chirp信號的分數階傅里葉分析[J].北京理工大學學報,1999,19(5):612-616.

[3]周剛毅,葉中付.線性調頻信號的調頻斜率估計方法[J].中國科學技術大學學報,2003,33(1):34-38.

[4]趙興浩,陶然,周思永,等.基于Radon-Ambiguity變換和分數階傅里葉變換的chirp信號檢測及多參數估計[J].北京理工大學學報,2003,23(3):371-374,377.

[5]李靖,王樹勛,汪飛.基于分數階傅里葉變換的chirp信號時頻分析[J].系統工程與電子技術,2005,27(6):988-990.

[6]朱全銀,鄧建平.基于分數階傅里葉變換的線性調頻干擾抑制[J].探測與控制學報,2009,31(1):10-14.

[7]金燕,黃振,陸建華.基于FRFT的線性調頻多徑信號分離算法[J].清華大學學報:自然科學版,2008,48(10):1617-1620.

[8]陶然,鄧兵,王越.分數階傅里葉變換及其應用[M].北京:清華大學出版社,2009.

[9]鄧兵,陶然,曲長文.分數階Fourier 域中不同調頻率多分量chirp信號間的遮蔽分析[J].電子學報,2007,35(6):1094-1098.