K分布雜波中分布式目標的Rao檢測

張曉利 關 鍵 何 友

(海軍航空工程學院電子信息工程系 煙臺 264001)

1 引言

當高分辨雷達(HRR)具有將一個目標分辨成在不同距離單元內的多散射中心的能力時，分布式目標的檢測問題便產生了。近年來出現了大量有關這方面的文獻。其中，以美國海軍研究實驗室的Gerlach和意大利的Conte, Maio等學者為代表的專家對分布式目標檢測問題進行了深入的研究，研究內容主要集中在分布式目標的回波模型、雜波統計規律、檢測器設計等方面。其中，文獻[1]在白噪聲背景下，假設分布式目標散射中心的空域分布密度為近似二項分布，推導了依賴于散射點分布密度的廣義似然比檢測器(SDD-GLRT)。文獻[2]在非高斯背景下，提出了具有恒虛警率(CFAR)特性的獨立于散射點分布密度的廣義似然比檢測器(NSDDGLRT)和SDD-GLRT。文獻[3]采用基于GLRT的“一步法”和“兩步法”給出了具有CFAR性能的檢測方案。“兩步法”GLRT在計算復雜度、實時性、檢測性能、硬件實現等方面都要明顯優于“一步法”GLRT。文獻[4]采用雜波分組的思想處理非均勻高斯雜波中分布式目標的檢測。文獻[5]將Rao檢驗和Wald檢驗應用到復合高斯雜波中距離擴展的分布式目標的檢測中，利用雜波分組的思想，得到了兩個自適應檢測器，即自適應Rao檢測器(ARAO-RX)和自適應Wald檢測器(AWALD-RX)。文獻[6]假設分布式目標是子空間信號，總的干擾是高斯色噪聲和雜波的疊加，雜波也是子空間信號，并且其所在的線性子空間是未知的；采用GLRT檢驗理論，在假設能夠得到只含有高斯色噪聲的輔助通道數據的前提下，分別在均勻背景和非均勻背景下推導了“一步法”GLRT和“兩步法”GLRT。仿真結果表明“一步法”GLRT的性能要好于“兩步法”GLRT，但是前者的計算量要遠大于后者。文獻[7]采用GLRT檢驗理論，研究了目標在距離和Doppler頻率維同時擴展的情況，針對目標散射體被建模為確定性未知和高斯隨機兩種情況進行了深入的研究。當目標速度未知時速度估計誤差造成方向矢量失配，文獻[8]研究了此種情況引起的方向矢量失配對GLRT的影響。文獻[9]在分析了寬帶雷達目標回波特點的基礎上，提出了一種基于順序統計量的距離擴展目標檢測器。

2 問題描述

2.1 信號模型

分布式目標的信號模型大都采用多主散射點(MDS)來建模，即分布式目標在每個距離分辨單元內的回波是該分辨單元內有限個孤立的強散射點回波的矢量和。假設分布式目標在距離和Doppler頻率維同時擴展，則分布式目標在第t (t=1,2,…,H)個距離分辨單元中回波的第n次采樣可以表示為

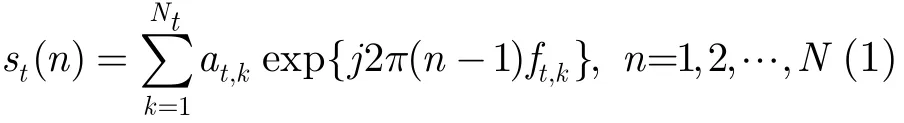
其中H是待檢測的分布式目標所占據的距離單元總數；t是距離單元編號；Nt是第t個距離單元內分布式目標的散射點總數目；at,k是第t個距離單元內第k個散射點的幅度；ft,k=fd(t, k)/fr為無量綱的數字頻率，fd(t, k)表示第t個距離單元內的第k個散射中心的Doppler頻率，fr為歸一化頻率。

式(1)可以等價地表示為

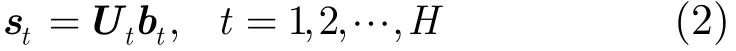
式(2)表明分布式目標可用子空間模型表示，即目標的回波處在由酉矩陣Ut的列矢量張成的信號子空間＜Ut＞上，酉矩陣Ut稱為模式矩陣；Nt×1維的列矢量bt稱為位置矢量。

2.2 雜波模型

一個球不變隨機變量的雷達雜波可以用如下的乘積模型來表示

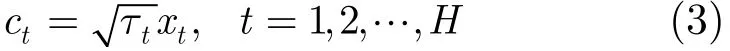
其中散斑分量xt是短相關時間的快起伏分量，有xt～CN(0,Mx)；紋理分量τt代表了檢測單元內的雜波功率水平，服從Gamma分布。上述乘積模型中的復高斯散斑分量與Gamma分布的紋理分量合成的結果就是K分布雜波。本文采用SIRP模型仿真K雜波作為HRR雜波的統計模型。

2.3 檢測問題描述

設觀測模型為

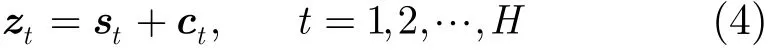
由式(4)可以將分布式目標的檢測問題歸結為如下的二元假設檢驗：

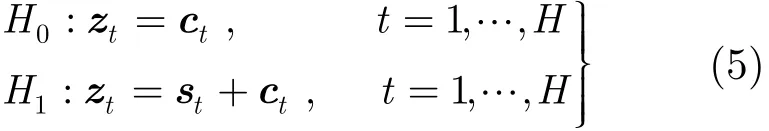
其中zt是基帶復數據觀測矢量。st是分布式目標的有用信號矢量，用式(2)表示。ct是HRR雜波，用式(3)表示。在上述觀測模型中，已知的數據有N×1維的復基帶數據觀測矢量zt，N×Nt維的模式矩陣Ut，即分布式目標所在的子空間。問題就是構造出檢驗統計量對式(5)的二元假設檢驗作出判決。

3 構建檢測器

目前大多數文獻對于式(5)的假設檢驗作出判決采用的是GLRT準則。然而GLRT不具有最優性能，本文用Rao檢驗(與GLRT有相同的漸進性能)對式(5)進行判決。一般而言Rao檢驗，與GLRT相比，易于計算。因為它不需要用估計H1假設下的未知參數，只需估計H0假設下的未知參數。本文用兩步法推導基于Rao檢驗的檢測器，步驟如圖1所示。

圖1 檢測器構造步驟

為方便起見，做如下假設：bR,t、bI,t分別表示bt(t=1…H)的實部和虛部；θr=[bR,1,bI,1,…,bR,H,bI,H]T是列矢量；θs=[τ1,…,τH]T是列矢量；θ=[θrT,]T。在此假設下的Rao檢驗為

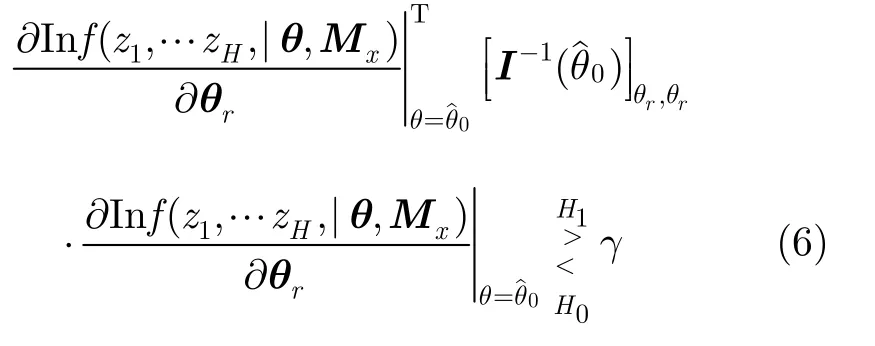
其中γ是檢測門限；f(z1,…,zHθ,Mx)是H1假設下的P D F；?/?θr=[?/?bR,1,?/?bI,1…?/?bR,H,?/?bI,H]T表示θr的梯度算子；θ0是θ在H0假設下的最大似然估計；I(θ)=I(θr, θs)是Fisher信息矩陣，可以寫成則

下面給出PDF和計算與θr有關的梯度算子。由假設可知H個分辨單元內的N×H維的觀測矩陣Z=(z1,z2,…,zH)的聯合條件PDF

由于現金流的不足或者擔保物品的缺乏，中小工業企業融資渠道少，多數只能從小額貸款公司或者商業銀行取得貸款，這些貸款的利率普遍較高。如果不能從銀行取得融資，那只能從親戚朋友借款，這部分的資金成本更高，企業業績如果沒有明顯的上升，等到借款償還期限一到，無法歸還借款，企業就面臨資金鏈斷裂，走向破產的邊緣。即使能周轉歸還借款，平時的資金成本也大幅侵蝕了企業利潤，導致企業效益低下，很難有較大的成長空間。

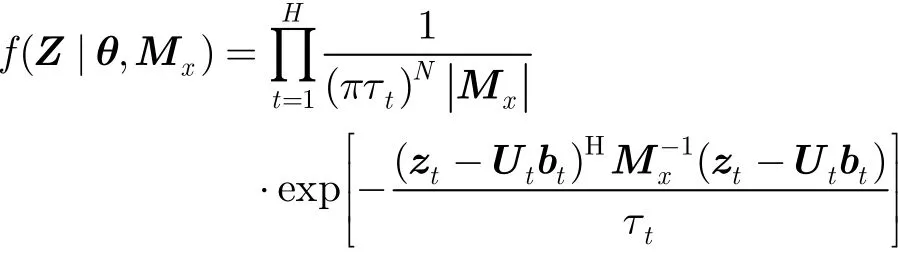
其中|.|表示矩陣的行列式。對其求導可得

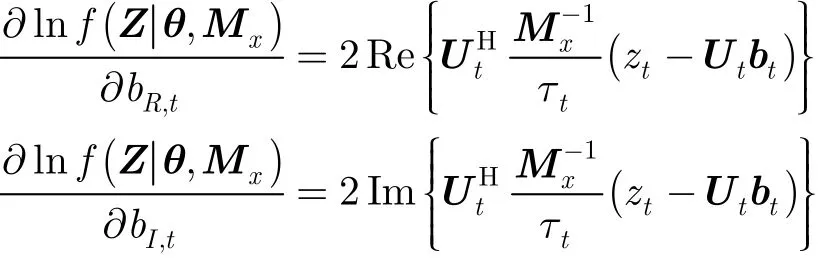
其中Re{.}和Im{.}分別表示自變量的實部和虛部。那么，

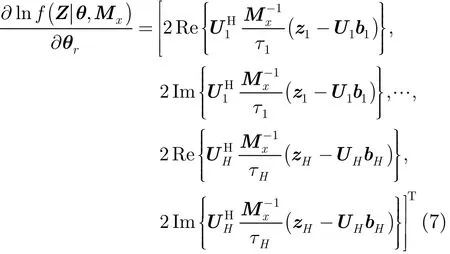
通過計算，可得Fisher信息矩陣為

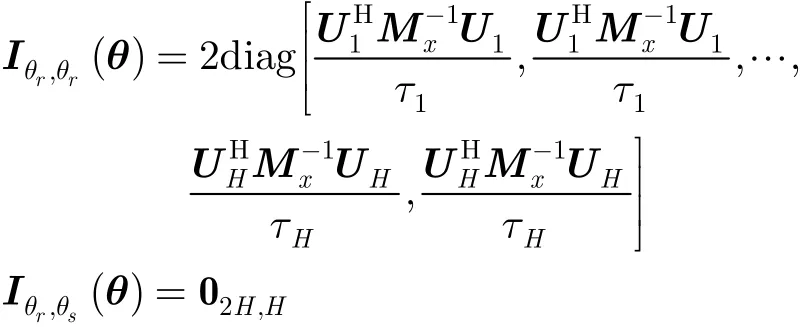
其中0n,m表示n×m維零矩陣；diag (δ1,…,δn)表示n×n維對角矩陣，其對角線元素為δ1,…,δn。則

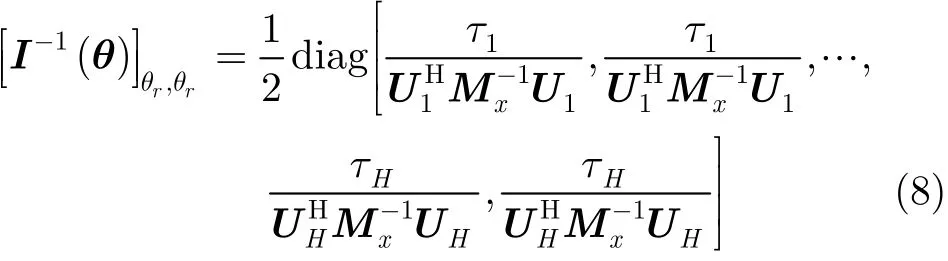
在H0假設下θ的最大似然估計為=其中表示H維列矢量[10]：

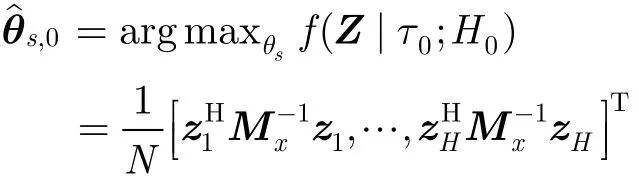
其中argmaxθs(?)表示θs取最大值時的標號。

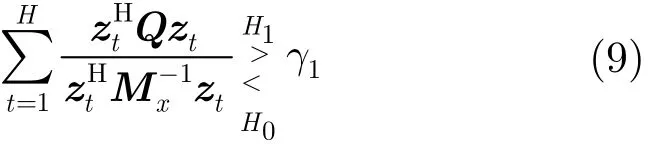
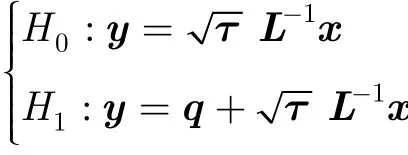
其中q=L?1s=(L?1U) b=Uqb是白化濾波器L?1輸出的信號矢量。q仍然是一個子空間信號，在由Uq=L?1U確定的信號子空間上，信號子空間U上的投q影矩陣為，則式(10)成立

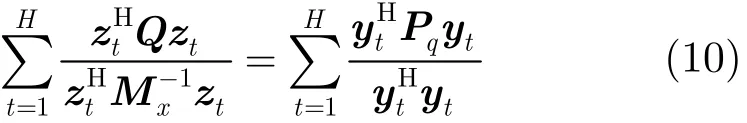
事實上，式(9)是對目標所占據的幾個距離單元分別做檢測，然后對各距離單元輸出的統計量進行非相參積累，形成最終的檢驗統計量，與門限進行比較。各個距離單元的檢驗統計量的計算是通過“白化”后信號向信號子空間投影的能量和“白化”后信號總能量之比來確定的。由式(10)可以看出，檢驗統計量是獨立于檢測單元的雜波功率水平，所設計的檢測器對于雜波功率水平具有CFAR特性。

像現有的雷達目標檢測文獻一樣，假設可以獲得與被檢測的主通道鄰近的HK個輔助通道的觀測zt(t=H+1,…,H(K+1))。該輔助通道數據不包含有用的目標信號，并且和待檢測的主通道雜波散斑分量有相同的協方差矩陣。則輔助通道數據的歸一化采樣協方差矩陣是主通道雜波散斑分量的協方差矩陣Mx的最大似然估計。按照“兩步法”的設計方法，用S代替式(9)給出的GRAO中的主通道雜波散斑分量的協方差矩陣Mx，得到距離擴展目標的自適應Rao檢測器(A-GRAO)為

4 仿真分析

由于本文所提出檢測器的檢測概率沒有解析表達式，本節采用Monte Carlo仿真對其檢測性能進行分析，并與以前的檢測器進行比較。

4.1 仿真參數設置

在Monte Carlo仿真中的參數設置為：各個散射點的幅度服從自由度為2 m的2χ起伏的獨立同分布的隨機矢量；H=4, H=3, H=2時各散射點的歸一化無量剛的數字頻率ft,k的取值分別見表1-表3。在表中同時給出了出現在各個距離分辨單元內的散射點總數目Nt的值。

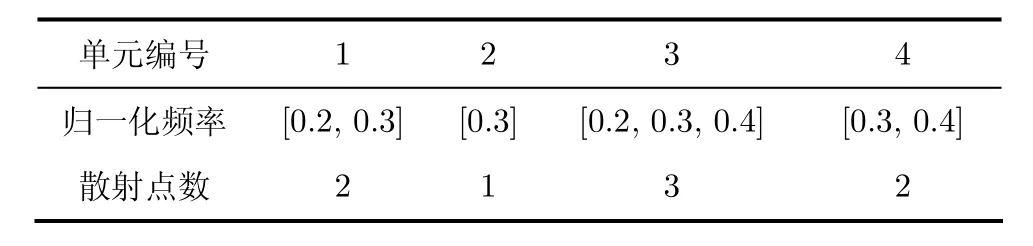
表1 H=4時散射點歸一化頻率

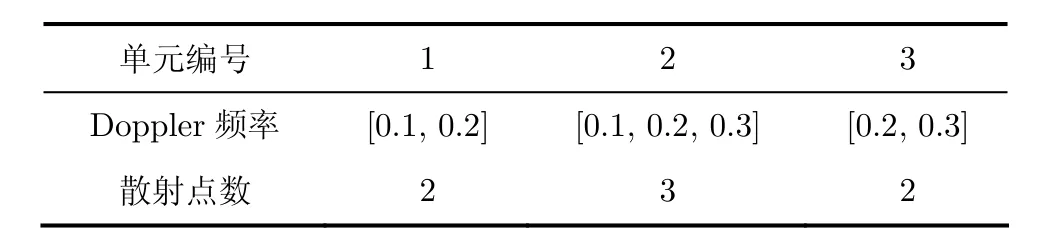
表2 H=3時散射點的歸一化頻率

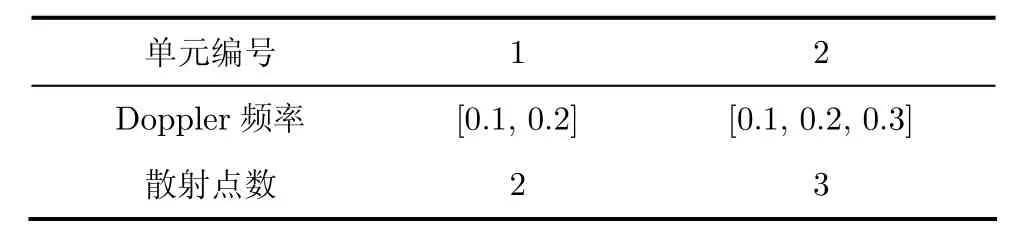
表3 H=2時散射點的歸一化頻率

K分布雜波的形狀參數為v，尺度參數為b，雜波的平均功率為σ2=E(τ)=v/ c2，其中c=b/2。信雜比SCR(dB)定義為

在仿真中設定虛警概率為Pfa=10?4。

4.2 仿真結果及分析

圖2仿真了距離和Doppler頻率維同時擴展的A-GRAO的檢測概率與信雜比曲線，其中H=4。仿真參數含義為：N是采樣數；K是輔助通道數；m是χ2起伏目標的自由度。為了進行比較，同時也仿真了僅在距離維擴展的ARAO-RX[5]和僅在Doppler頻率維擴展的MSD[10]。在仿真ARAO-RX的性能時，假設H=4，其導向矢量為p =[1,ej2πfd,…,ej(N?1)2πfd]T，fd是所有散射點的歸一化Doppler頻率，在仿真中設fd=0.1。在仿真MSD的性能時，假設目標能量都集中在一個距離單元，每個距離單元內的雜波能量也相應地提高了H倍；頻率維擴展為2維子空間，在仿真中取表1的距離單元編號為1的那組數據。從圖2可以看出，A-GRAO的性能要明顯好于ARAO-RX與MSD的性能。事實上，目標建模為在距離維和Doppler維上的擴展更加符合實際情況，減少了由于引入模型引起的誤差，所以會提高檢測概率，當然這也是以增加計算量為代價的。下面將分析雜波和目標參數對A-GRAO檢測性能的影響。

從圖3和圖4中可以看出增加相干積累數N和增加距離分辨單元數H都可以明顯改善A-GRAO的檢測性能。仿真中雜波的平均功率為1。N對檢測性能的影響非常明顯，隨著N的減少，檢測性能顯著下降。在目標總能量相同的情況下，目標占據的距離單元總數越多，檢測概率越高；也就是說，雷達的分辨率越高，檢測概率也就越高。

圖5分析了不同的MDS模型對A-GRAO檢測性能的影響。MDS模型如表4所示，其中標明每個距離單元中的目標能量與目標總能量之比。目標的總能量為所有散射點的能量和，即。每個散射點的能量為。從圖5的仿真結果可以看出，當距離分辨單元總數相同時，目標能量在不同距離單元中的不同分布對檢測概率的影響相對于其它參數的影響來說是很小的。

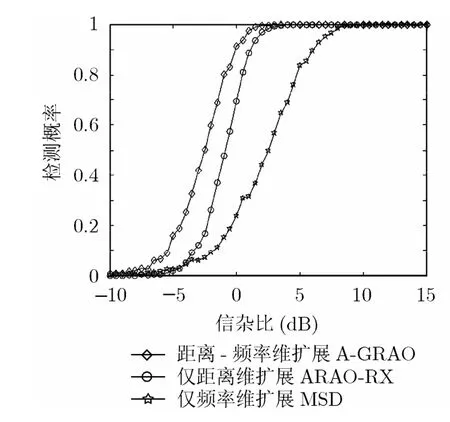
圖2 A-GRAO、ARAO-RX和MSD的檢測概率與信雜比曲線，N=8，K=8，v=2，m=1

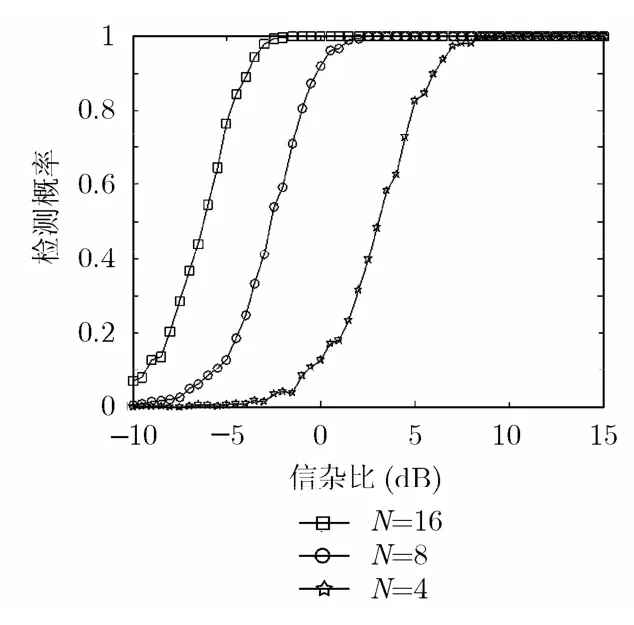
圖3 A-GRAO的檢測概率與信雜比曲線，H=4, K=8, v=2, m=1, N為參數

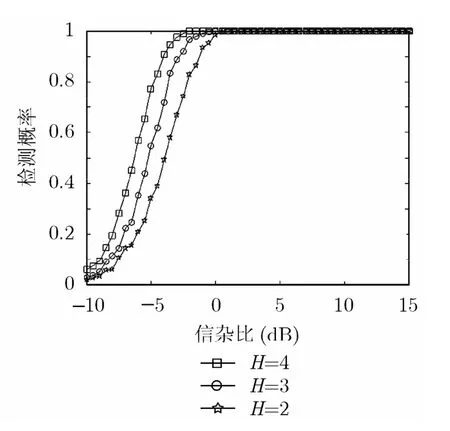
圖4 A-GRAO的檢測概率與信雜比曲線，N=16, K=8, v=2, m=1, H為參數

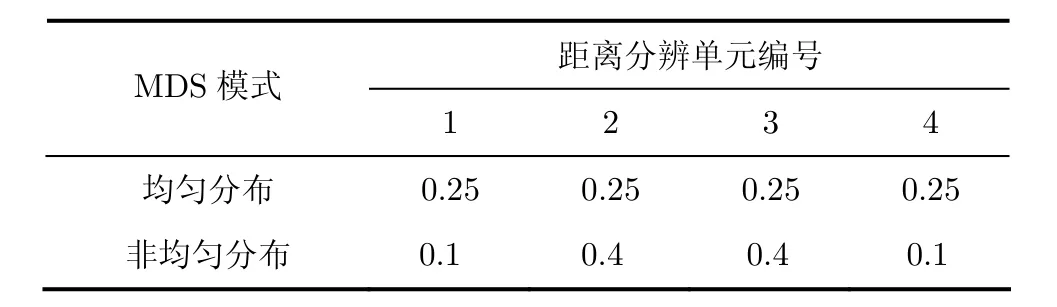
表4 H=4時各距離單元的能量

圖5 A-GRAO的檢測概率與信雜比曲線， H=4, N=16, K=8, v=2, m=1

圖6是分析雜波的形狀系數v對A-GRAO檢測性能的影響。由圖6可見雜波越尖銳(v越小)，檢測概率越高，原因是v越小，雜波的非高斯特征越明顯，所設計的A-GRAO就能充分發揮作用。即A-GRAO具有在強非高斯雜波中檢測微弱目標的能力。文獻[2,4]給出的兩個距離擴展的分布式目標的檢測器具有相類似的結果。

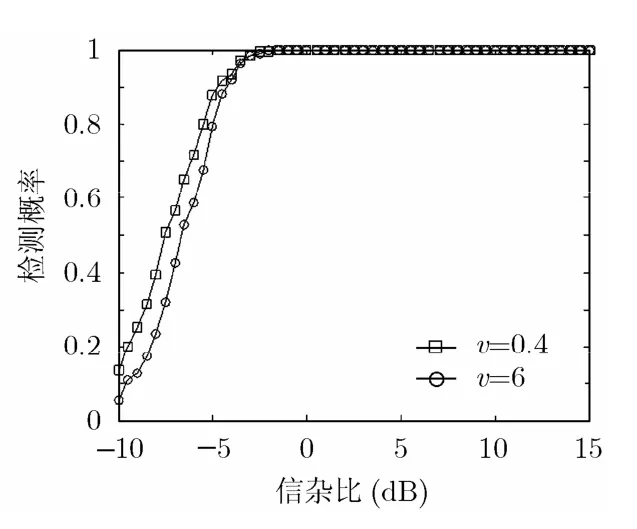
圖6 A-GRAO的檢測概率與信雜比曲線， H=4, K=8, N=16, m=1, v為參數

5 結束語

本文用子空間模型對分布式目標建模更符合實際情況；Rao檢驗不需要估計H1假設下的未知參數，減少了計算負擔。GRAO具有對雜波功率水平的CFAR特性。經仿真驗證：A-GRAO具有良好的檢測性能；在增加相干積累數和增加距離分辨單元數的情況下都可以改善其檢測性能；K分布越尖銳，A-GRAO檢測概率越高；在目標所占的距離單元數目一定的情況下，目標能量在各個距離單元之間的分布在對檢測概率的影響有限。

[1] Gerlach K, Steiner M J, and Lin F C. Detection of a spatially distributed target in white noise[J]. IEEE Signal Processing Letters, 1997, 4(7): 198-200.

[2] Gerlach K. Spatially distributed targets detection in non-Gaussian Clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 926-934.

[3] Conte E, De Maio A, and Ricci G. GLRT-based adaptive detection algorithms for range-spread targets[J]. IEEE Transactions on Signal Processing, 2001, 49(7): 1336-1348.

[4] Conte E, De Maio A, and Ricci G. CFAR detection of distributed targets in non-Gaussian disturbance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002,38(2): 612-621.

[5] Conte E and De Maio A. Distributed target detection in compound-Gaussian noise with Rao and Wald tests[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003,39(2): 568-582.

[6] Bandiera F, De Maio A, and Greco A S, et al.. Adaptive radar detection of distributed targets in homogeneous and partially homogeneous noise plus subspace interference[J]. IEEE Transactions on Signal Processing, 2007, 55(4): 1223-1237.

[7] Bon N, Khenchaf A, and Garello R. GLRT subspace detection for range and doppler distributed targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008,44(2): 678-695.

[8] 陳遠征, 范紅旗, 付強. 復合高斯雜波下距離擴展目標的OMGLRT[J]. 信號處理, 2008, 24(5): 718-721.Chen Yuan-zheng, Fan Hong-qi, and Fu Qiang. Orderstatistic-based detector for range spread target[J]. Signal Processing, 2008, 24(5): 718-721.

[9] 戴奉周, 劉宏偉, 吳順君. 一種基于順序統計量的距離擴展目標檢測器[J]. 電子與信息學報, 2009, 31(10): 2488-2492.Dai Feng-zhou, Liu Hong-wei, and Wu Shun-jun. OM-GLRT of range spread targets in compound Gaussian clutter[J].Journal of Electronics & Information Technology, 2009,31(10): 2488-2492.

[10] Gini F and Farina A. Vector subspace detection in compound-Gaussian clutter. Part I: Survey and new results.IEEE Transactions on Aerospace and Electronic Systems [J].2002, 38(4): 1295-1311.