基于剪切波的肝臟纖維化超聲粘彈性檢測系統

譚偉，韓曉東，程剛，Hazard Christopher

1 通用電氣中國研發中心，中國 ，上海，201203 2 通用電氣全球研發中心，美國

基于剪切波的肝臟纖維化超聲粘彈性檢測系統

【作 者】譚偉1，韓曉東1，程剛1，Hazard Christopher2

1 通用電氣中國研發中心，中國 ，上海，201203 2 通用電氣全球研發中心，美國

描述了一種基于目前醫用超聲硬件的肝臟粘彈性測試系統。該系統利用超聲輻射力推動肝臟軟組織形成瞬態響應，探測該響應中的剪切波傳播，從而估算肝臟組織的彈性和粘性。本研究證實肝臟的楊氏模量和粘性系數可以通過剪切波成功定量檢測，并且可以用目前已有的醫用超聲系統實現而無需額外硬件，從而為醫生提供一種新的廉價而有效便捷的診斷手段。

超聲；肝臟；纖維化；肝硬化；彈性測試；瞬態彈性成像

1 應用背景

病毒性肝炎(主要包括乙型肝炎和丙型肝炎) 以及其它形式的肝損傷是中國最嚴重的公共衛生問題之一。肝纖維化則是包括乙肝和丙肝在內的各種慢性肝病損傷修復過程的共同病理表現，是肝臟病情進展的關鍵階段。臨床研究表明，因為體內存在纖維降解機制，肝纖維化甚至早期肝硬化可以通過藥物治療減輕或逆轉[11]，防止其演變為死亡率很高的肝硬化和肝癌，改善肝病患者的預后。因此，肝纖維化的早期診斷對截斷整個肝病發展鏈舉足輕重。

長期以來，基于METAVIR評估體系的肝臟組織活檢一直是評價肝纖維化程度的黃金標準。但是活檢10%-20%的患者會出現局部疼痛，少數患者還可出現較嚴重的并發癥，很多患者因此拒絕接受活檢，更不可能作為治療效果追蹤和評估的頻繁性檢驗手段。而且，肝纖維化活檢僅采樣肝臟局部的一個點，即使取材合格，病理診斷仍常取決于檢驗人員的主觀性，重復性差，只有大約65%的標本纖維化分期診斷能被不同的病理科醫生認同。

昂貴的CT和MR不利于常規篩查。而目前常規超聲對肝病的診斷，主要集中在形態變化和血流變化，如肝臟門靜脈和附近消化系統靜脈血流血壓的判斷[10]。然而肝組織出現纖維化病變時，其回聲特性變化并不明顯，對血流血壓的影響也幾乎不能檢測，所以基于B超和多普勒超聲的纖維化的早期評估難以有實質結果。而近些年的生理病理研究發現，在這個階段肝組織的粘彈性已經發生了比較明顯的改變。因此，無創定量測量肝臟組織的粘彈性對肝纖維化乃至肝癌的早期診斷、制定醫療措施以及療效的追蹤評估具有重要意義[9]。

2 肝臟纖維化的定量檢測

超聲彈性成像的研究和應用是醫學超聲研究的熱點，并且在近年來發展出多個種類。然而真正通過FDA認證并真正商業化并應用到臨床的非常有限。由于技術和法規兩方面的限制，目前產品中普遍應用的仍然是非定量化的應變成像，不能對粘彈性作定量化檢測。我們基于肝纖維化疾病掃查的特殊需要，放棄以成像為目標，僅僅對檢測點提供平均彈性合粘性參量，在達到臨床目的的同時避免了以上技術和法規的限制。

2.1軟組織在超聲脈沖沖擊刺激下的響應

為從肝臟軟組織的動態響應中提取其機械特性的信息，首先需要在組織內部產生一個與其時間常數相當的力的作用。任何形式的電磁波、彈性縱波、聲波等以振動形式傳播的能量，在遇到吸收性介質時都會產生單向的輻射力。聚焦的超聲聲束則可在軟組織中形成聲場分布，并進一步產生聲學輻射力[3]。超聲換能器的聲場遵從Khokhlov-Zabolotskaja-Kuznetsov(KZK)方程[4]，求解出聲壓后聲學輻射力可寫為[7]：

其中z表示沿超聲探頭的軸向坐標；Fz表示z方向的力；上畫線表示在超聲時段內的平均值。p表示聲壓；ρ代表肝組織密度；c代表聲速；τ=t-z/c；b表示介質的有效吸收系數。

在力Fz作用下，介質的位移在聚焦點附近滿足：

其中ct=√μ/ρ代表剪切波的傳播速度；μ表示剪切模量；η是剪切粘度；uz是z方向的位移分量；為拉普拉斯算子。在Voigt粘彈性模型的假設下，剪切波的速度可以推算為：

此式表明，剪切波速度是彈性、粘性以及剪切波頻率的函數。通過測量剪切波并在頻域上分解得到各頻率上的剪切波速度V（ω）由非線性擬合即可得到剪切模量μ和剪切粘度η。

（1）和（2）式的求解有兩個步驟:基于特定超聲探頭的聲場計算和輻射力作用下位移的計算。這兩步均牽涉到很多非線性參數，求解通常有兩種選擇:通過簡化利用格林函數獲得解析解，或者利用有限元方法數值求解，相關的內容將在另文詳述。圖 1分別是這兩種方法得到的剪切波傳播示例。仿真結果表明，材料除了彈性，其粘性對剪切波的形態也有較大影響。在肝臟的彈性（4 kPa～21 kPa）和粘性(1 Pa.s～4 Pa.s)范圍內，需要妥然選擇脈沖重復頻率（PRF），以在盡量避免回波干擾的同時維持足夠的采樣帶寬。因此，針對肝臟的粘性、檢測深度、彈性（決定剪切波速度因而系統最低采樣頻率）以及距主要邊界的距離等參數，對探頭和系統作優化設計。以上的解析模型和有限元模型則提供了這樣的優化設計工具。由式(3)可以看到，剪切波的傳播速度不僅依賴于彈性，也同時依賴于粘性。目前基于剪切波的超聲彈性研究 等均忽略粘性影響[7、9、12]，以簡化公式計算彈性。以上的有限元模型顯示，在某些范圍上這種簡化會導致10%左右的誤差。

圖1 仿真計算：長超聲脈沖作用后的剪切波Fig.1 Simulation: Shear Wave Generated by Long Ultrasound Pushing Pulse

2.2肝臟楊氏模量通過醫用超聲檢測的機理

2.2.1 系統工作機理

超聲是超聲換能器加以振蕩電信號后產生的機械振動在媒介中的傳播。理想的正弦信號在途中任一點的運動是雙向的。然而由于媒介的衰減作用，聲波在途中被組織吸收，從而其強度不可避免地隨深度衰減，形成聲場的梯度分布。正是這種梯度形成了相對超聲的高頻振動是單向的作用力——聲輻射力[2]。運動開始時是沿超聲發射軸向（Z方向）的位移，帶動鄰近的彈性組織，這種位移產生兩個效應：一是軸向的壓縮拉伸，從而以縱波方式向前傳播，二是由于和橫向相鄰組織的剪切應力，產生橫向傳播的剪切波，體現為橫向各點沿Z方向按時間順序的剪切位移。理論分析和實驗表明，對肝臟而言剪切波的速度一般在1～6 m/s。在醫用超聲上，這樣的傳播完全可以用既有硬件檢測到。

整個檢測系統如圖2所示。在超聲探頭上根據中軸線定義有微小間距的位置A和B。首先通過掃描控制在位置A和B分別發射檢測脈沖并沿這兩條線采集回聲。采集的回聲作為參考信號。

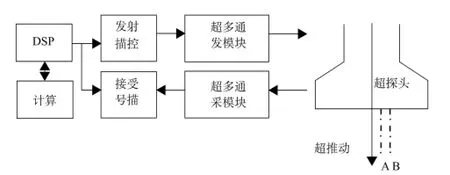
圖2 肝臟彈性的超聲檢測框圖Fig.2 Diagram of Detecting Liver Elasticity with Ultrasound

圖3 中的第二步是發射一段較長時間的聚焦超聲脈沖。與普通的脈沖多普勒模式下發射的一到兩個周期的脈沖不同，這段脈沖可長達數百μs。由于軟組織粘性的影響，長時間脈沖可以產生較大幅度的軸向位移，從而可導致隨之的剪切波有較大的信噪比。在這段脈沖作用下，將首先產生約數百μs的持續輻射力，肝臟組織的剪切波將從中軸線向兩邊橫向傳播。這段脈沖聚焦點的選擇可以是固定的，也可以是沿中軸線的數個點依次聚焦，后者可以形成更大幅度的剪切波。

圖3 超聲掃描時序Fig.3 Ultrasound Scan Seqeunce

第三步是分別在A點和B點探測一定深度上的位移對時間的曲線，其原理與脈沖多普勒的原理類似。所不同的只是這里檢測的是各點的位移，而非速度。

2.2.2 位移檢測方法

超聲波傳播并產生反射和散射的介質可認為是一團隨機分布的粒子。在某個位置一組隨機粒子的平均振動速度可以估計為[3]：

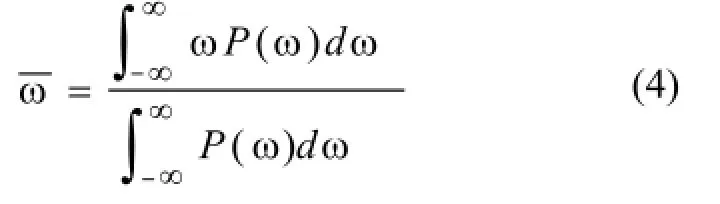
其中P(ω)是功率密度。直觀上理解，這只是整個頻域上角速度的平均。

利用維納－肯琴定理，上式可以簡化為

R(t)是信號的自相關函數。

這樣的形式仍然不便于計算。由于R可以進一步近似為R(τ)=│R(τ)│ejφ(τ)，上式可以簡化成：

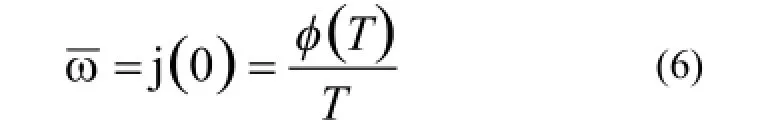
其中T是超聲脈沖發射的時間間隔。由此可以推出平均位移為：

在具體實現時，從超聲陣列傳感器接受到的射頻信號Z經過超聲前端電路的放大和模數轉換的處理，往往進一步經過正交解調成為IQ信號，如圖 4所示。

圖4 信號分解Fig.4 Signal Decomposition

IQ自相關函數的角度可以寫成

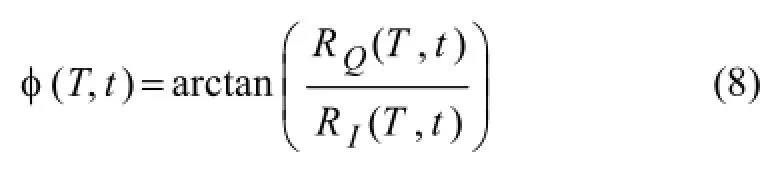
由此一組點上的平均位移可以寫成：

fc為超聲中心頻率，c為介質中的聲速。信號的自相關函數則可進一步寫成：

經過次采樣后的形式為

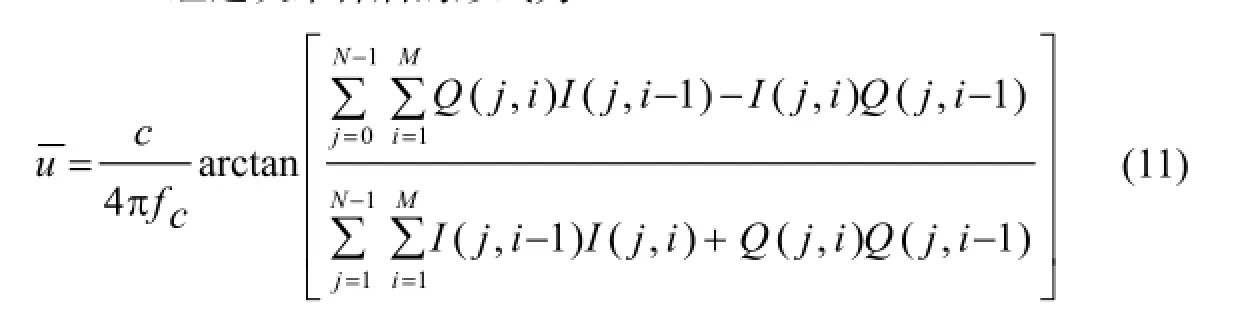
計算組織位移的另一種方法是基于時間移動的互相關方法，在具體應用上可以和上面的方法作一些折衷。

3 實驗

3.1粘彈性超聲仿體的制作

為了驗證這里開發的肝臟組織彈性(硬度)無創測量技術，我們做了大量基于超聲仿體(phantom)和動物肝臟的實驗。我們分別自制以及從美國CIRS公司（Computerized Imaging Reference Systems, Inc）定制了彈性仿體對應于METAVIR標準中的F1到F4的主要階段。文獻[8]提供了對超聲彈性仿體制作較深入的研究。我們在研究中進一步發現，通過特殊交聯劑不但可以大幅改善仿體的穩定性和形態，而且仿體的彈性和粘性可以通過溫度和紫外線等手段外部調制。圖5是仿體的加工過程和成品。主要原材料有明膠、瓊脂和玻璃棉，玻璃棉主要作用是散射超聲信號。如圖 5(a)中所示先把不同原料按照一定的工藝流程，分別加熱到各自適當的溫度，進行攪拌混合，然后加入適量的交聯劑，放入水平振蕩箱中冷卻凝固，最后利用模具成型并由0.2 mm鋼絲切割而成。通過改變各種原料的比例和交聯劑，控制交聯過程等，可以制出各種彈性的超聲仿體。其聲速約1500 m/s、聲衰減系數約3 dB/MHz.cm，密度約1000kg/m^3，均和肝臟組織相一致。各彈性仿體都在中科院硅酸巖研究所力學實驗室進行標定。

圖5 超聲彈性仿體的定制Fig.5 Fabrication of Ultrasound Elasticity Phantoms

3.2仿體實驗結果

配制的超聲彈性仿體經過機械測試，獲得的楊氏模量如圖 6所示。

圖6 仿體彈性的機械測試結果Fig.6 Mechanical Test Result of Phantom Elasticity

隨即這些仿體用上文所描述的超聲系統進行了測試。在A點獲得的剪切波如圖7所示。從圖上可以直觀地看到剪切波傳播并衰減的趨勢。根據A、B兩個位置位移峰值出現的時間差，可以計算出剪切波傳播的速度。另一種更可靠的方法是對這兩條波形用傅立葉變換作頻率分解，從而綜合考慮整個波形的移動而不僅僅依靠最大位移值點。

圖7中x軸方向是時間軸；y方向是沿A線的深度軸，300的位置對應于2厘米；z軸為位移。圖中靠近超聲探頭的區域仍然有大幅度的位移，這是由于沿途組織吸收了能量，在聲場梯度下產生的輻射力作用的結果。這些區域雖然沒有聚焦，但是由于靠近探頭，位移依然較大。通過改進探頭設計，調節探頭的聚焦數（focal number)，可以讓焦點處的能量更為集中，從而在同樣的信噪比下在沿途組織上可降低能量消耗。另一方面，聚焦點處不是一個點而是一個條狀區域，可提供一種改善結果的方法。圖中從深度200到350的區域剪切波的位置基本一致，簡單的平均可以獲得更穩定的結果。

最后，經過對獲得的剪切波進行計算后，得到的楊氏模量如圖 8所示。對比圖 6可以看到二者非常接近。由于聲速和泊松比的估算有一定誤差，當歸一化后，機械測試和超聲測試的結果非常接近。

圖7 A線上的位移Fig.7 Displacement Along Position A

圖8 仿體彈性的超聲測試結果Fig.8 Ultrasound Test Result of the Phantom Elasticity

3.3動物肝臟實驗結果

我們進一步在豬的肝臟上進行了實驗，結果如圖 9所示。其中的位移曲線分別距離超聲探頭的中心位置2.4 mm和4.8 mm。可以看到在300 μs的長脈沖作用下，豬肝組織在聚焦點附近隨時間位移。這些位移曲線明顯反應了剪切波傳播的過程。通過分解各種頻率成分得到圖9(b)的相速度信息，對式（3）的非線性模型通過最優化方法進行逆問題求解，計算得到的剪切模量約5.12 kPa，而粘性系數為1.5 Pa.s。

3.4安全性測試

3.3.1 聲壓測量以及MI和Ispta指標計算

以上實驗的聲壓用水聽器在水槽中進行了測量。使用通用電氣醫療系統的LOGIQ9醫用超聲系統以及10L線型探頭，在2.5 cm的聲學聚焦點可以對發射的功率進行0%到100%的調節。實驗中我們在最大功率時測得7 MPa的聚焦聲壓。

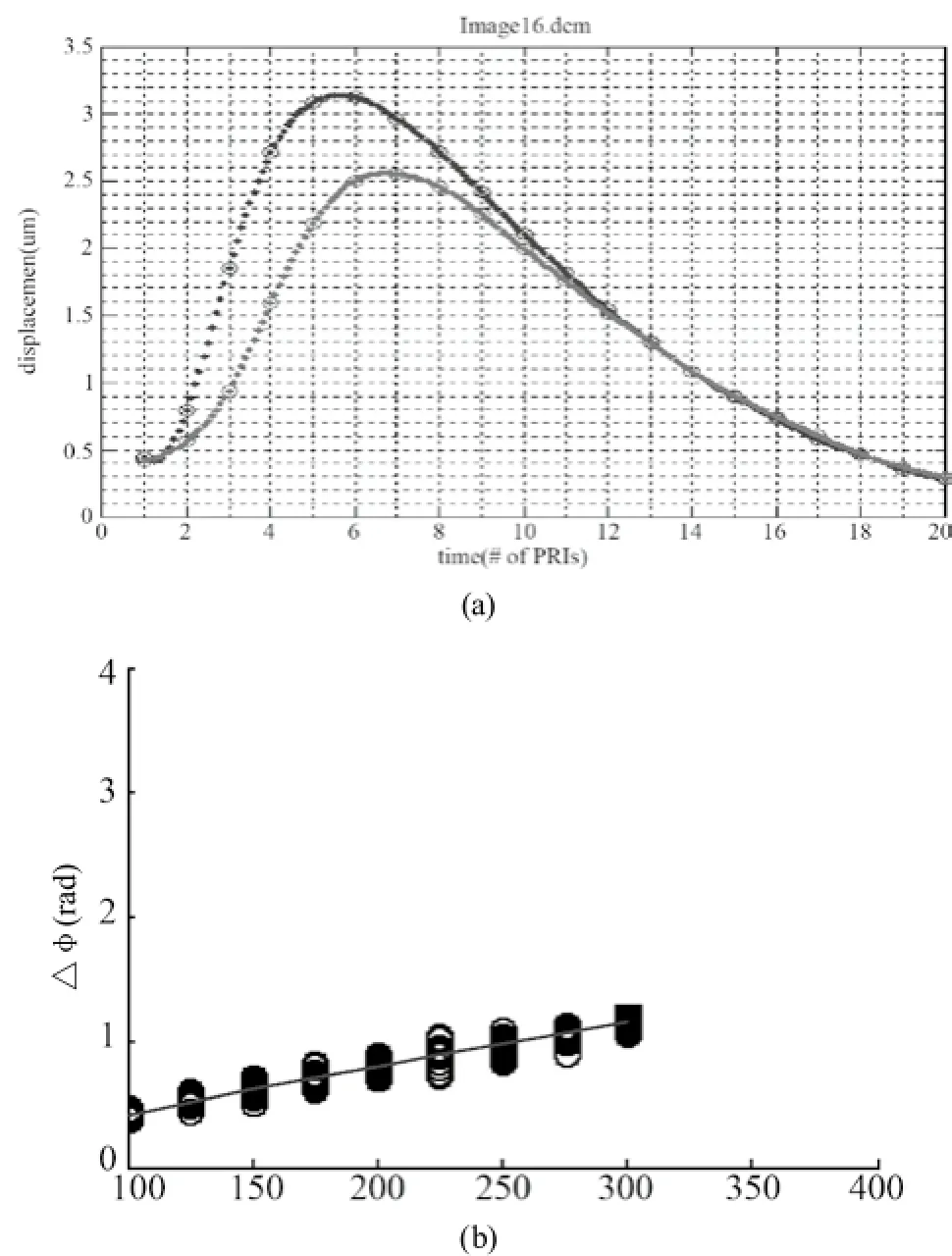
圖9 肝臟彈性的超聲測試結果Fig.9 Ultrasound Test Result of Liver Elasticity

FDA對醫用超聲的MI指標限制為2.0，Ispta為720mW/cm2。在以上的實驗中7 MPa的水中聲壓在考慮人體約0.3 dB/MHz/cm的衰減后在2.6 cm處的聲壓估計為4.5 MPa。

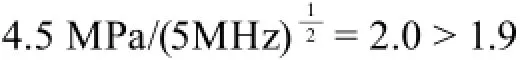
計算得到的值略微超過 FDA限制。然而由于我們在信噪比上尚有很大余地，完全可以略微調低發射功率以滿足該限制。

Ispta的計算根據FDA定義：

Ispta = 4.5 MPa2/(2*ro*c)*tpush/texperiment

由于我們不對肝臟成像，而僅僅是測量一個彈性值，理想狀態下僅需要發射一次長脈沖，這個值可以通過調節占空比任意縮小。在實驗中占空比為0.001時Ispta因此僅為340.3 mW/cm2，完全滿足FDA要求。

人的肝臟一般在肋骨以內1 cm處，最大尺寸達15 cm左右。盡管肝纖維化有彌散性，在足夠深度上測試其彈性無疑會有更高的代表性。為提高穿透性，我們進一步選擇了2 MHz以及機械聚焦在6 cm的探頭。實驗證明在5到6 cm的深度本文中的測試方法仍然具有很好的信噪比，能夠可靠地檢測肝臟彈性。

4 總結與展望

本文通過理論分析，用超聲測試肝臟組織的彈性和粘性的實驗方法，可定量判斷肝纖維化程度。理論分析和實驗結果均證明，利用現有的醫學超聲系統硬件，可以僅通過軟件控制和數據處理實現對彈性剪切波傳播速度的測量，利用非線型模型逆問題求解實現對粘彈性進行定量檢測，達到對醫學診斷上有意義的結果。該技術尤其適合肝病肆虐的發展中國家。該檢測的便捷性使得它可以納入到慢性肝病者的日常例行體檢中，做到早診斷、早預防和早治療。

[1] Jorgen Arendt Jensen, Estimation of blood Velocities using Ultrasound, Cambridge University Press, 1996

[2] Chihiro Kasai, et al, Real-time two dimensional blood flow imaging using an autocorrelation technique[J], IEEE trans. Ultra, 1985, 458-463.

[3] G. R. Torr, The acoustic radiation force[J], American Journal of Physics, 1984, 52(5): 402-408.

[4] Polina Solomonnovna Landa, Nonlinear Oscillations and Waves in Dynamical Systems[M]. Kluwer Academic Publisher, 1996.

[5] Novikov BK, Rudenko OV, Timoshenko VI. Nonlinear underwater acoustics[M]. New York: American Institute of Physics, 1987.

[6] Arnold P.G. Hoeks, et al. Comparison of the performance of the RF cross correlation and Doppler autocorrelation technique to estimate the mean velocity of simulated ultrasound signals[J], Ultra. in Med. & Biol, 1993, 19 ( 9):727-740.

[7] Armen P. Sarvazyan, Oleg v. Rudenko, et al. Shear wave elasticity imaging: A new ultrasonic technology of medical diagnostics[J]. Ultrasound in Med. & Biol, 1998, 24(9): 1419-1435.

[8] Timothy J. Hall, Mehmet Bilgen, et al. Phantom Materials for Elastography, IEEE Trans. Ultra. Fer. and Freq. Contr., November 1997, 44(6): 1355-1365.

[9] Marie Muller, Jean-Luc Gennison, Thomas Defieux, et al. Quantitative viscoelasticity mapping of human liver using supersonic shear imaging: Preliminary in vivo feasability study[J]. Ultrasound in Medicine & Biology, 2008,35 (2), 219-229.

[10] 解育新. 肝纖維化的超聲診斷現狀及進展[J]. 醫學影像學, 2008, l4(6): 942-944.

[11] 曾民德, 陸倫根, 茅益民. 肝纖維化的診斷方法及其評估[J]. 中國肝臟學, 2006, 11(2):102-205.

[12] Fahey BJ, Nightingale KR, Palmeri ML, et al, Acoustic radiation force impulse imaging of myocardial radio-frequency ablation: initial in vivo results[J]. IEEE UFFC, 2005, 52(4): 631-641.

Shearwave-Based Ultrasound Viscoelasticity Measurement System for Evaluation of Liver Fibrosis

【Writers】Wei Tan1, Xiaodong Han1, Gang Cheng1, Hazard Christopher2

1 General Electric Global Research Center in China, Shanghai, 201203 2 General Electric Global Research Center in USA

【Abstract】This paper describes a liver elasticity and viscosity measurement system based on existing medical ultrasound platforms. This system relies on acoustic radiation force to invoke transient response on soft tissue, and employs displacement estimation algorithms to detect the propagation of shear wave. The research proves that the velocity of the shear wave may serve as a reliable estimation of the Young's modulus and viscosity coefficient of the liver tissue, and existing commercial products may be easily adapted to support this technique without extra hardware cost.

ultrasound, liver fi brosis, cirrhosis, elasticity measurement, transient elastography

R318.03；R318.6

A

10.3969/j.isnn.1671-7104.2010.05.005

1671-7104(2010)05-0330-05

2010-05-09

譚偉，E-mail:wei.tan@ge.com