一種生長法快速構造三角網的算法研究

王會然

(河北省地礦局測繪院，河北廊坊 065000)

一種生長法快速構造三角網的算法研究

王會然?

(河北省地礦局測繪院，河北廊坊 065000)

針對DEM制作過程中大數據量構建三角網效率問題，提出了一種多級索引支持的三角網生長算法，該算法邏輯結構簡單，編程實現容易，可以驗正該算法比通用軟件提供的相應未優化算法速度提高很多。

不規則三角網；Delaunay三角網；索引

1 引 言

數字高程模型(DEM)，是一種描述地形起伏的數學模型。其可分為規則格網、不規則三角網和等高線幾種類型。規則格網具有結構簡單、直觀的特點，但在對復雜地形特征表達和分析方面，不規則三角網與其他兩種方法相比，具有較高的精度和效率，目前Delaunay三角網是公認的最優三角網。通過離散高程點和特征線、等高線構造生成三角網，已有許多專家進行了算法研究和改進，其方法類型主要有3類；

①分而治之法(由Shamos和Hoey提出)，即對大量點分塊構網，再合并成一個整體。構網時采用局部優化(Lop)算法保證其成為Delaunay三角網。其運算中大量使用遞歸，故實現起來有困難。

②數據點漸次插入算法(由Lawson提出)，其方法是先找到最外層點作多邊形將所有點包括進去形成一個凸殼。在此基礎上構網，將內部點逐一加入，并采用Lop算法保證其成為Delaunay三角網，此算法簡單，但效率不高。

③三角網生長算法，該方法算法簡便，如果不加優化，則效率亦不高。本文就針對生長算法，提出了一種優化算法——區域索引加正方形搜索區域的方法。使生長法具有很高的效率。

2 關于Delaunay三角網

Delaunay三角網為相互鄰接不重疊的三角形的集合。每一個三角形的外接圓內不包含其他點。Delaunay三角形有3個相鄰點連接而成，這3個相鄰頂點對應的Voronoi多邊形有一個公共的頂點，此頂點也是Delaunay三角形外接圓的圓心。Delaunay法則就是在構造三角網時，確保每個三角形內角是銳角或者三邊近似相等，避免鈍角和過小銳角出現。

3 三角網的構建算法

三角網生長算法，就是首先在已知離散點中任選一點做起始點，找到其最近點，以兩點連線作為起始基線，在基線右側，應用Delaunay法則搜索第三點，生成Delaunay三角形(每條基線方向如圖1，AB為起始基線)，再以三角形新的兩條邊作為新基線(AC和CB)，重復該過程，直到所有基線處理完畢。

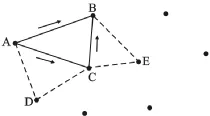
圖1 三基形生長示意圖

4 算法優化及實現

4.1 構網方法優化

(1)索引的建立:對采集的高程點(或等高線點)進行預處理。將數據讀入后，按坐標計算范圍，并統計點數，提出對話框詢問是否建立點的分區索引以及要建立索引的分區行數和列數，根據點密度情況人工輸入合理值。這里所說的對點進行分區，就是對所有點按坐標最小和最大所限定的范圍在水平和垂直兩方向等分，把這個范圍均分成若干行若干列，見圖2。對一個點，根據點的兩坐標值與分區邊緣比較一下，落在哪個區就統計在哪個區內，每個區有多少個點記錄在一個由區號標識的數組變量中，每個區中的點，也記錄在一個由區號標識的數組變量中。該數組變量除了包括點號和坐標外，還包括一個屬性值表示該點是否參與過一次構網，初始值為0，表示未構網。因為分區數和區內點數是在運行中得到的，故這些變量都用到動態數組。

圖2 對離散點進行索引示意圖

(2)搜索正方形的使用:對要搜索的點，如果在一個正方形范圍內進行搜索，搜到后再做點與基線關系的有關計算，則會使計算量進一步減少。以合適點為中心做一正方形，通過對正方形4頂點計算落在哪幾個分區中這一簡單比較運算，得到該正方形所用到的分區，在分區中將落在正方形中的點找到，再進行點與基線關系的運算，找出最佳點。開始構網時，是在所有點中先任選一個點(當然也可以選最左上一個點)，在所有點中找到離它最近的點，此兩點為起始邊(起始生長基線，之后的生長基線統稱基線)，起始點可不在整個區域邊緣，如取點時取文件的第一個點，該點就可能在中間某一位置，如圖3，A為起始點，B為與A的最近點，線段AB為起始生長基線，圖中搜索正方形中心點選基線的中點，邊長選已分區水平方向邊長的1/4，當正方形中無點或無合適點(如在AB所在直線左側有點，右側沒發現點，或有點但它們已經構網且夠兩次即該點已完成了構網，當前基線不再構網，要進行基線轉移，要到其他未完成的三角形上去找新基線)時，對正方形按一定數量增大邊長(但不能增大超過三角網預設最大邊長一定量級，如兩倍，如果超過，基線右側點有可能與基線距離會超過最大邊長允許值，這個最大搜索正方形邊長也是在開始根據三角網允許最大邊長大小給定的)，直到找到合適點或右側無點(見圖4和圖5)。圖4中，虛線正方形表示許可的最大搜索正方形。在圖3中，如當不是開始構網而是在構網中間時段，則AB基線表示當前生長基線。圖3為正方形落在一個分區內的情景，當然還可以落在幾個分區內，即跨幾個分區，見圖6。

圖3 搜索正方形構建示意圖

圖4 當前生長基線AB右側無點的情況

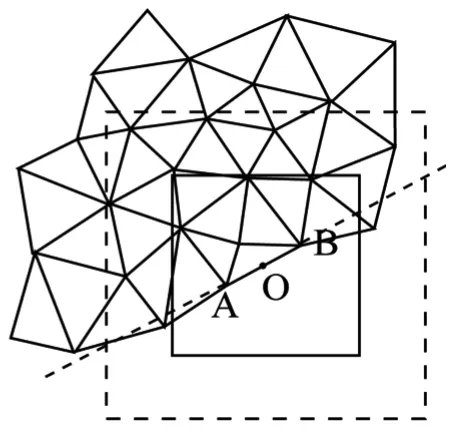
圖5 當前生長基線AB右側有點 但再沒有未曾構網點的情況

圖6 搜索正方形跨幾個索引區的情形

4.2 算法實現

當無優化時，構造三角網如圖7，當前基線為AB，為了找到符合條件的C點，需要對所選點與基線位置關系進行判斷，將最好的點如C作為下一個構網點，這就要將可能構網的所有點都要進行這種判斷計算，如圖6中的D、E、F、G、H、I……等等，即每構一個新三角形，就要對可能點進行遍歷搜索。當構網點數很大時，構網速度和效率就會很低。本方法所論述就是為改善這種情況的優化方法。首先進行分區:對讀入數據變量應包括:點號(按讀入順序)、x、y、z三坐標、區編號q(初始值為0)，假如x、y坐標最小值和最大值分別為xmin和xmax，ymin和ymax，如果分成m行n列，則共有m×n分區，記△x＝(xmax－xmin)/n，△y＝(ymax－ymin)/m，當讀入數據后再給出行列數，這些值就可以算出。接著就是對所有點按分區歸檔，進行第一次遍歷數據，對一個點(x，y)，當xmin＋(kh－1)×△x≤x＜xmin＋kh×△x則點所在區落在第kh列(1≤kh≤n的整數)，同理，當ymin＋(kl－1)×△y≤y＜ymin＋kl×△y則點所在區落在第kl行(1≤kl≤m的整數)。當kh和kl求得后，分區號q＝kh×n＋kl，將q值賦與該點區編號。用一個數組變量記錄每個區的點數累加值。接著進行第二次遍歷數據，根據所得每個區的點數累加值d(q)，取d(q)最大者，創建分區點信息數組p[q，d(q)，5]，第三維中包括點號dh、三坐標x、y、z、是否曾構網判斷值gw。如果為了節省內存，可將第三維數組分開表示為:pdh[q，d(q)，1]、px[q，d(q)，1]、py[q，d(q)，1]、pz[q，d (q)，1]、pgw[q，d(q)，1]，這樣就可以用整型變量表示點號和用短整型表示點已構網次數。

圖7 構造三角網無優化時情況示意圖

下面是搜索正方形建立及搜索構網點的具體過程:構網的第一個點從坐標最外圍為原則如左上、左下等，這樣構網是從邊緣開時的。如果第一個點按文件數據順序，則第一個點可能出現在區域內任一位置，這樣構網可能在區域內開始，兩種情況沒實質差別。第一個點確定后，先判斷它在哪個索引區，然后在該區和所有相鄰區內(有時該點可能與相鄰區內某點最近)查找最近點，兩點連線作為第一條生長基線。以基線中心點坐標為中心，構造搜索正方形，正方形起始邊長，可取分區的寬的四分之一。構造正方形時，以基線中點坐標，由邊推算出對應四角點坐標，然后對正方形四頂點坐標值與各分區邊縱橫坐標進行比較，確定該正方形所在的分區(一個或幾個)。在這些分區內，將所有區內點與正方形邊范圍比較，找出所有在正方形內的點。當無點時，把正方形按起始邊長的一半擴大正方形，直到找到點。找到點后，計算所有在正方形內點與基線關系，選出離基線最近的點，直到右側無點。對找到的點，計算該點與基線關系，應滿足以下兩種要求:①該點要在基線的右側。方法是按下面函數計算: F(x，y)＝y＋Ax＋B。式中A＝(y2－y1)/(x1－x2)；B＝(x1×y2－x2×y1)/(x2－x1)。 x1，x2，y1，y2分別為基線兩端點坐標。當F(x，y)〉0時，該點在基線左側，相反在右側。F(x，y)＝0表示該點在基線上。②讀取該點是否已構網狀態，判斷該點是否參與構網，未曾構網時直接進行下一步。當已構網時在已構網邊中判斷是否與該基線兩點中任意點達到兩次，達到兩次時，該點不再使用。③該點為頂點的角要取最大的。根據余弦定理c2＝a2＋b2－2abcosC可得cosC＝(a2＋b2－c2)/2ab，取cosC最小的，此時C值最大，cosC＜0時說明C角是鈍角，這里不排除鈍角這一情況，當點位不均勻或等高線平行性發生突變時，會出現這種情況。對合適的點，構建好三角形后，以新邊為基線，重復以上過程，直到把所有邊都進行了搜點構網。

5 結 論

該算法運算公式簡單，可容易地用VC＋＋和VB編寫程序實現，由于建立格網索引只需兩次遍歷所有點，在對搜索正方形時，也只用一些簡單坐標比較就可以在一個或幾個分區內找到在搜索正方形內的所有點，這樣就避免了在大量的點中判斷符合與基線構造三角形的條件計算問題。當點數很大時，設有一萬個點甚至幾十萬個，如果不優化，每構一個三角形都要對所有點進行是否在基線右側、點是否已構網兩次、到基線距離是否最小這些判斷，其中第1和第3兩項有公式運算，構網效率就很低。當用該方法優化時，先生成搜索正方形，再定位其4個角點所在索引格，然后在所有索引格中找正方形內點，最后在正方形內點進行上述判斷。所處理點數與正方形內點數有關，所以當正方形不用擴大時，其邊長為一個索引格寬1/4，如果我們共有M×N索引格，且我們索引時在水平和垂直兩個方向上索引格邊長大致相當，且我們同時設定高程點分布是比較均勻的(不均勻也沒關系，點的稀密也使落在正方形內的點同樣多或少，不影響最終全部處理的時間，這里假設這種情況，是為了好理解)，那么，每個正方形占全部點分布面積的比例為:1/(M×N×16)，也就是說，對點進行計算時所用點數為原來的1/(M×N×16)，由此可知，速度可以提高到(M×N×16)倍，值得一提的是，沒有計算生成搜索正方形、判斷正方形所在索引格、在索引格中找正方形中的點這些時間，實際上，我們處理的是當數據量很大時的情況，當數據量不大時，什么算法都不會有明顯優勢(計算機很快)。數據很大時每個索引格不會太小(至少幾百個點)，對于生成正方形是一個加減法運算，對正方形所在索引格判斷也只是4個點坐標與幾個索引格坐標比較，對落在正形內點判斷也只是幾個索引(1～4)內點與正方形邊坐標比較，這些做比較的次數不多且簡單，會使最終效果與上面估計的有所降低，但不是很大。對于正方形需增大找點的情況并不多，實際上每個起始正方形內往往會有上百個點。由此可知，此方法與不進行優化相比，速度提高幾十倍到幾百倍并不困難。只是注意，我們對索引格建立時，要大小合理，當太大時M和N都變小，根據效率倍數估算(M×N×16)可知會使率降低，但當太小時，會使最終搜索正方形內點太少，正方形內出現無點情況就增多，擴大正方形情況也就多了，同時相關比較運算也會增多。所以合適的索引格大小，也是保證最佳速度的關鍵。

6 存在問題

由于索引建立和其他相關數組建立，需要更多的內存，主要體現在:①對每個點要增加一個索引區號分量(整型)，增加內存1/7。②分區后又按區進行統計，等于是復制一遍數據，對于新增的判斷構網次數分量，可能其他方法也都用到，這里不妨也算上，共增加內存1.2倍。③為索引等服務的少量變量。最后估計多用內存近1.5倍。但現在計算機的內存已很大，這方面已不是主要問題。還有，沒有論述對所有點進行優化篩選，通過篩選，可以把一些對相對平坦或坡度均勻的多余點進行去除。同時沒有考慮特征線的情況，希望以后把這方面內容考慮進去(就是一條特征線間點是一定要連線構網的，這項做起來相對簡單些。)以使算法更加完善。

[1]彭李，劉少華，盧學軍.一種基于動態正方形的TIN的構建算法[J].現代測繪，第30卷第2期，2007

[2]唐麗玉，朱泉鋒，石松.基于STL的DelaunayTIN構建的研究與實現[J].遙感技術與應用，第20卷第3期，2005

Research of an Algorithm to the TIN Construction with the Growing Method

Wang HuiRan
(The institute of surverying and mapping of geologic Bureau of Hebei Province，LangFang 065000，China)

Aiming at inefficiency of triangulation construction for large data in the DEM production process，a triangulation growth algorithm supported by multi－level index is proposed in this paper.The logical structure of the algorithm is simple so that it can be implemented easily by programming.It can be tested that the new method will process more faster than the corresponding algorithm provided by some common softwares.

Irregular Triangulation；Delaunay Triangulation；Index

1672－8262(2010)02－146－04

P209

A

2009—06—29

王會然(1966—)，男，工程師，現從事測繪遙感工作。