T形航路船舶交通通過能力分析

文／韓 鵬 馬海洋 馬 勇

針對中國航道船舶交通現狀，提出T形航路船舶交通通過能力的研究課題，建立T形航路船舶交通通過能力模型，最后借助計算機語言實現模型的求解。

In view of vessel traff i c situation in China, the article proposes a research subject about vessel transit capacity in T-type channel and sets up a transit capacity model. And results can be given by using computer language.

航道通過能力的研究主要分為以下三種：以單位時間內通過的客運人數/貨物噸數來表示基于吞吐量的航道通過能力；以航道所能通行的最大尺度的船型來表示基于單船的航道通過能力；以單位時間內通過的船舶艘數來表示基于船舶交通的交通通過能力。其中航路船舶交通通過能力又分為單航路和多航路交通通過能力研究，單航路指單向或雙向航路，多航路包括T形及十字形航路等。

國外對航路船舶交通通過能力的研究起步較早，且大多以單、雙向航路船舶交通通過能力研究為主。對于多航路船舶交通，主要以日本稻石正明[1]等學者建立的船舶行為集群模型為代表，國內主要以余勁[2]等船舶交通流的到船分布和船頭間距分布特性研究為代表。本文嘗試借鑒國內外學者的先進研究手段，展開T形航路船舶交通通過能力的研究。

一、T形航路船舶交通規律分析

1.排隊論的引入

A.k.Erlang于1909年創立了排隊論[3]。排隊是人們日常生活中常見的現象，多航路船舶交通亦是一種較為復雜的排隊現象。產生排隊現象的兩個主要因素是資源的有限性和人們對資源的需求。此外，服務機構的管理水平、運行效率等也會明顯影響排隊現象的產生。排隊論的研究目的就是尋找各種排隊系統的規律性，以調整和控制排隊系統，使之最大限度地發揮服務系統的效率。

2.T形航路船舶交通流概況

T形航路內船舶交通情況復雜，一般分為以下幾種：圖1（1）為最簡單的航路船舶交通流分布情況，即簡化為兩支船舶交通流交匯情況，方向可向東或向西；圖1（2）為T形航路內三支船舶交通流分布情況，有一支船舶交通流不受其他船舶交通流的干擾，航路內有兩支船舶交通流交匯；圖2為本文所研究的T形航路基本交通流分布示意圖，在T形航路內船舶為三支交通流交匯。

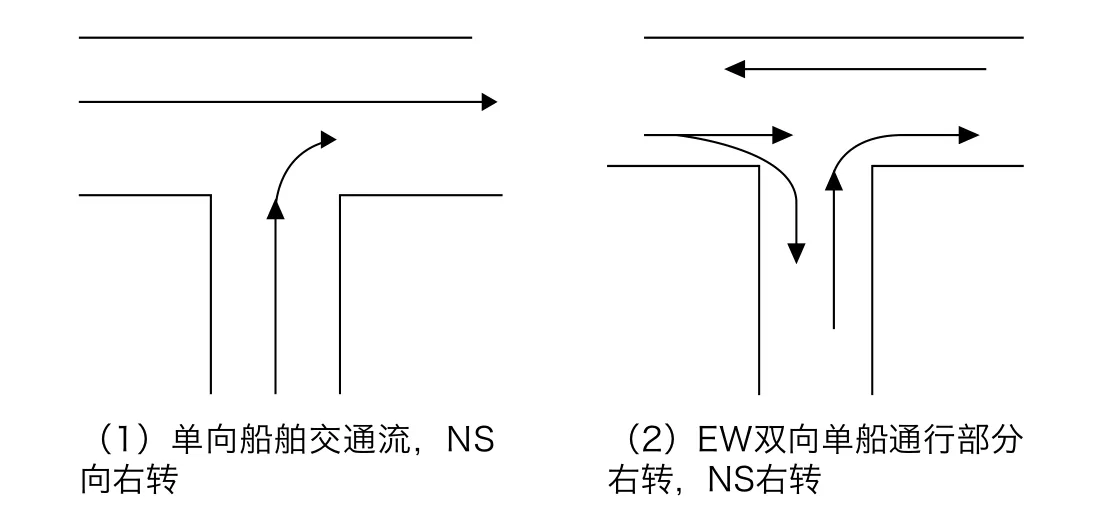
圖1 T形航路船舶交通流部分流向

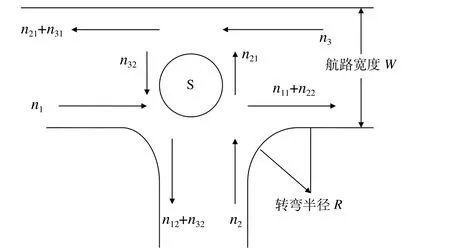
圖2 T形航路內船舶交通流分布

3.T形航路內船舶到達規律

對于一組實測交通數據x1，x2，…，xn，一般滿足某種特定的分布。交通工程中常用χ2檢驗加以驗證，這種方法不論是連續型還是離散型分布都可應用。本文采用χ2檢驗擬合船舶到達規律，T形航路內船舶到達為相互獨立事件，到達規律需在大量實測基礎上求得，一般服從相互獨立、同分布的Poisson分布，其分布的概率母函數、均值和方差分別是

4.T形航路內船舶服務規律

T形航路交叉區域內的船舶服務一般為單船服務，且為三支交通流循環服務，某一船舶在交叉區域駛過的距離除以其行駛速度即為該船舶在交叉區域的服務時間。服務的時間為一隨機變量，其分布的概率母函數、均值和方差分別為當T形航路為某一交通流內單船完成服務、轉向為其他隊列的船舶服務時，會出現一定時間的服務間歇，即交叉區域服務轉換時間，該隨機變量分布的概率母函數、均值和方差分別是本文結合T形航路內船舶交通的實際特點，求得服務率β為

式中：k為船舶列數(也代表T形航路服務窗口數，取k=1)；m為船舶類型數； Vi為第i類船舶的船速；pi為第i類船舶出現的概率；Si為第i類船舶駛過交叉區域的通行距離。

二、T形航路船舶交通通過能力模型的建立

1.服務的時間Vi, m

假定在某一交通流服務期間（τm＝tm-tm-1）有ζi(τm)艘船舶進入第i列交通流，記其中的第l艘船舶（l＝1,2,…,ζi(τm)）接受服務需要時間為Si,l，而在這Si,l期間內又有船舶進入第i列交通流。經計算得，船舶進入第i列交通流接受服務的時間Vi,m為

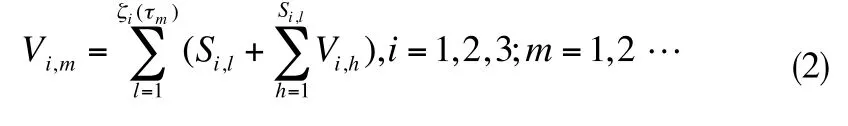
2.第 j 列交通流中平均船舶數

記μi(n)為交叉區域從第i列向第i+1列交通流服務轉換的時間，μj(μi)，ηj(vi)分別為在μi，vi時間內進入第j列交通流的船舶數量，則在tn+1時刻有

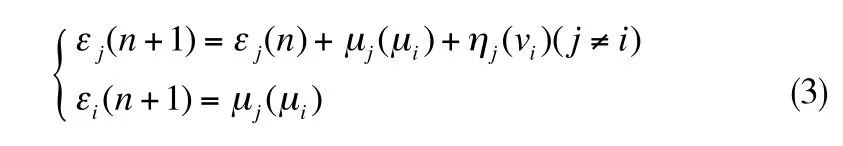
設在tn時刻第i列交通流開始接受服務，經計算得第j列交通流中平均船舶數為

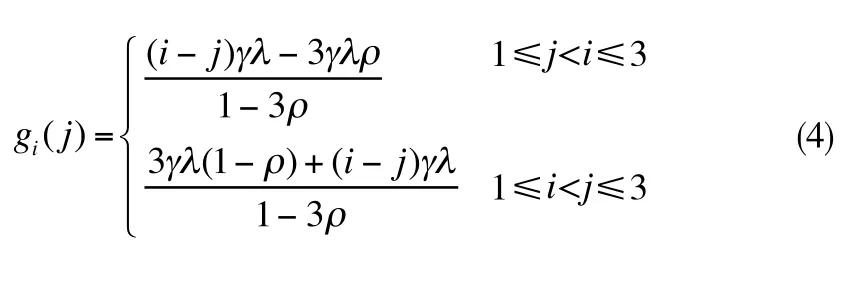
3.船舶接受服務的過程

若第i列交通流在tn時刻駛入并在tn1時刻駛離交叉區域，由于在tn1時刻仍然有船舶到達第i列交通流，因此，在tn1時刻新進入第i列交通流的船舶艘數為εi(n1)，而其駛離交叉區域的時刻為tn2，船舶接受服務的過程如圖3所示：

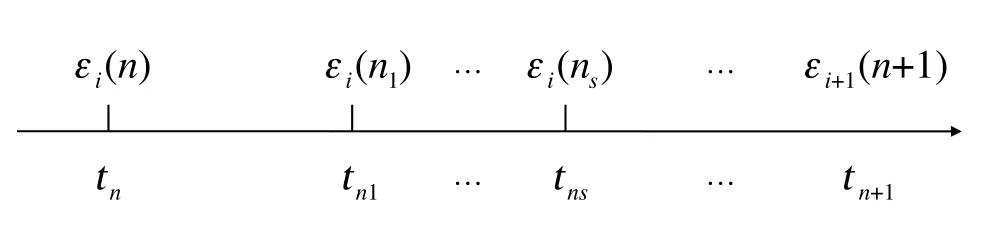
圖3 第i列船舶交通流接受服務的過程

4.T形航路內船舶交通通過能力N

若第i列交通流中第l艘船舶在第τm時間段（τm＝τmτm-1）進入該交通流，并在 時刻接受服務，則第l艘船舶等待接受服務的時間為

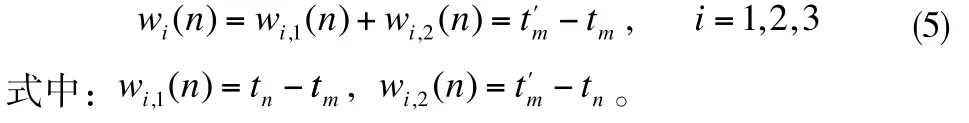
在此期間，有關系式：

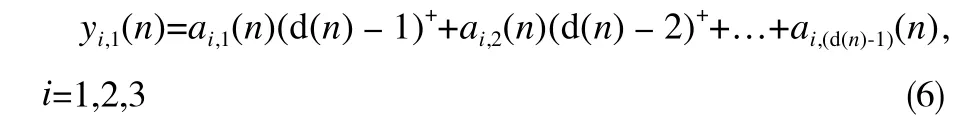
式中：d(n)為第i列交通流在時刻tn再次接受服務的時間；ai,m(n)為在τm時間內進入第i列交通流的船舶數量。

同理，在第i列交通流接受服務期間，新進隊列船舶等待接受服務時，有關系式:

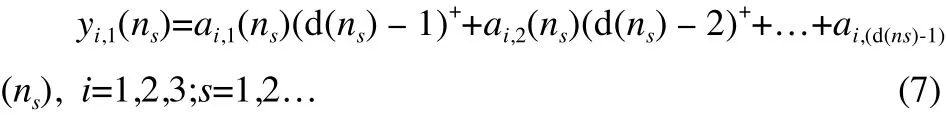
由式 (6)、(7)計算得wi,1(n)的平均值，同理，可計算得wi,2(n)的平均值，由此，船舶在交通流中接受服務的時間為

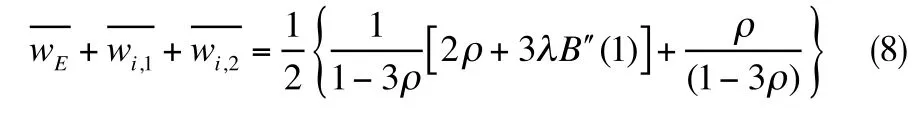
在系統中，船舶到達服從泊松分布，系統中所能容納的船舶數量為

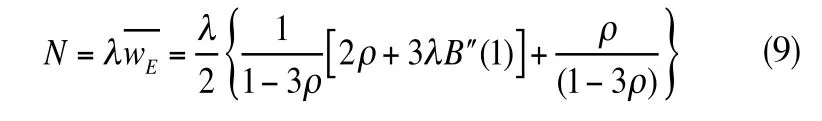
三、模型的實現

對于T形航路交通通過能力的計算，本文通過VC++編程加以實現。利用本模型可計算在一定約束性條件及相關航行參數下的T形航路船舶的交通通過能力。T形航路船舶交通通過能力求解流程如圖4所示。

依據本模型可求解不同船型（標準、中等、小型）在不同通過參數情況下對應的T形航路船舶日服務艘數。如對于1000 t級中型船舶，若橫流速度為0.33 m/s，可得出該T形航路日船舶交通通過能力為152艘；選取5000 t級標準船型，則在不同的設定參數（橫流分別為0.755 m/s、0.13 m/s）下對應的T形航路日船舶交通通過能力分別為110艘和124艘。經驗證，運算結果與目前我國主要T形航路理論日服務艘數基本一致。另外，通過模型也可驗證：T形航路服務水平越高，橫流越小，船舶交通通過能力越大。

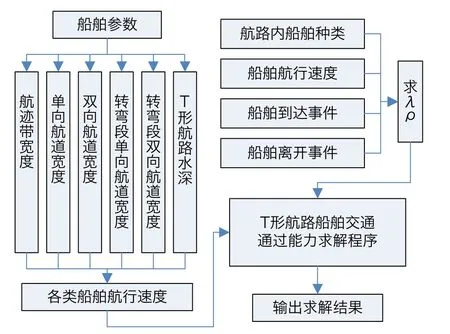
圖4 T形航路船舶交通通過能力求解流程

[1] 稻石正明, 今宿智仁. 船舶群と船舶群遭遇シミユレ—シヨン[C].日本航海學會論文集, 2003:21-26.

[2] 余勁. 西江航道船舶流的概率分布特性[J]. 交通運輸工程學報,2006(2):19-20.

[3] 陸鳳山. 排隊論及其應用[M]. 長沙:湖南科學技術出版社,1984:303-321.