基于多元線性回歸分析的風機噪聲預測的研究

徐冠基，柏 林，劉小峰，董鵬飛

（重慶大學測試中心，重慶 400030）

1 引 言

能源是國民經濟和社會發展的重要戰略物資，隨著煤、石油等不可再生能源短缺越來越嚴重，能源問題已成為當今世界矚目的焦點，各國都在促進可再生能源的發展。風力資源是取之不盡用之不竭的，利用風力發電可以減少環境污染，節省煤炭、石油等常規能源。風力發電技術成熟，在可再生能源中成本相對較低，有著廣闊的發展前景。而風力發電機產生的噪聲問題作為風力發電場選址過程中的主要矛盾之一，限制了風力發電機在全球范圍內大規模布置。因此，對風力發電機進行聲發射的測試和評估，對風力發電場的選址具有重要的現實意義[1-3]。

國際電工委員會于1998年制定了“IEC 61400-11，風力發電機組－第11節：聲學噪聲測量技術”國際標準第一版，以后不斷改進，對風力發電機聲發射評估過程做出了詳細規定，以保證風力發電機聲發射評估過程的一致性和結果的可比性[4]。

該文在仔細研究了IEC 61400-11標準后，提出采用多元線性回歸分析的方法對風力發電機在開機狀態下產生噪聲的聲壓級進行預測，對多元線性回歸分析的模型和求解過程進行了建模，求得線性回歸方程。

2 多元線性回歸分析法

多元線性回歸分析是預測分析最常用的方法之一，其基本原理就是：首先對歷史數據進行分析，建立數學模型；其次，用最小二乘法求取模型中的未知參數；最后，用回歸模型對因變量的變化趨勢做出預測。多元線性分析是應用最廣泛的統計學分支之一，其主要用途包括用于描述解釋現象、用于預測、用于控制等[5]。

2.1 多元線性回歸模型的建立[6-7]

多元線性回歸分析是研究一個因變y和多個自變量（x1，x2，x3，…，xm）之間線性關系的方法。假設在實際問題中，已經確定了對因變量Y有影響的主要因素有 p-1 個，記為 X1，X2，X3，…，Xp-1，則它們之間可以建立線性回歸模型：

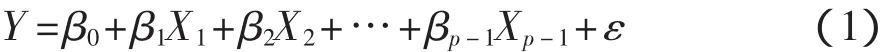
式中：β0，β1，β2，…，βp-1——未知參數，稱為回歸系數；ε——每次觀測時的隨機誤差，滿足Gauss-Markov假設，即 ε～N（0，σ2）。

在觀測得到n組相互獨立的實驗數據（xi1，xi2，xi3，…，xip-1）（i=1，2，…，n）后，便可得：

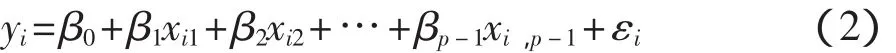
寫成矩陣形式為：

其中：

2.2 用最小二乘法求取回歸系數[8]

令Q=εTε=（Y-Xβ）T（Y-Xβ），則Q為n次觀測誤差的平方和，Q應該越小越好，于是可以取使Q取得最小值時的作為系數矩陣β的點估計。

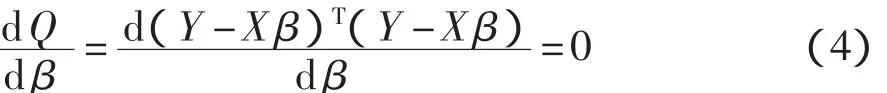
從而得到經驗回歸方程：

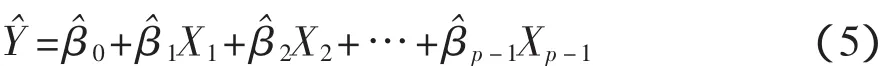
3 多元線性回歸分析在風力發電機噪聲預測中的應用

3.1 風機聲發射評估過程的研究

目前世界各國對風機聲發射評估過程的要求，都以IEC的“61400風力發電機系統-第11節：聲學噪聲測量技術”（簡稱IEC 61400-11國際標準）中的測量分析方法為主要依據。

為了全面體現風機噪聲的特點，標準規定需要對以下參數做出測量：

（1）聲學參數。風力發電機組產生的噪聲的聲壓。

（2）非聲參數。包括風力發電機組的輸出功率、轉速、機艙風速、槳距角、偏航角、溫度、氣壓、測風塔風速、風向。

根據標準的規定，必須對風力發電機組產生的噪聲的等效連續A計權聲壓級（簡稱聲壓級，用LAeq表示）做出計算。

風力發電機、風電場都有其獨特的噪聲發生機理：周圍環境通常為山村或田園，背景噪聲較低，但隨風速變化而改變（由氣流作用于植物或地表引起），并且具有掩蔽效應。

因此，風機噪聲的測試所需儀器設備較多、較雜。如“WINDTEST Kaiser-Wilhelm-KoogGmbH”，該公司在進行某次風機噪聲認證時所使用的聲壓測量儀器、傳感器如表1所示。

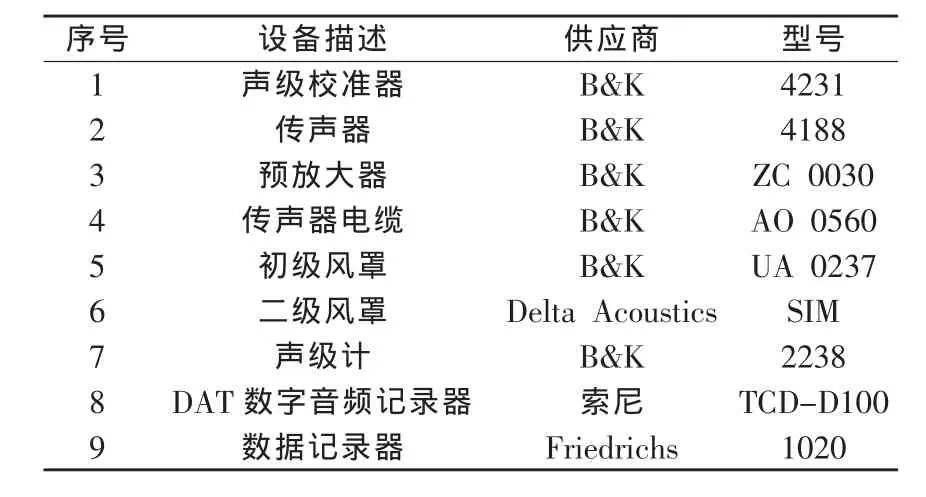
表1 “WINDTEST Kaiser-Wilhelm-Koog”使用的測量設備

由此可見，在實際測量工作中，聲壓的測量是不易實現的。因此，可以用多元線性回歸分析的方法，通過較易實現的非聲學參數的測量近似推斷出LAeq。具體過程如圖1所示。

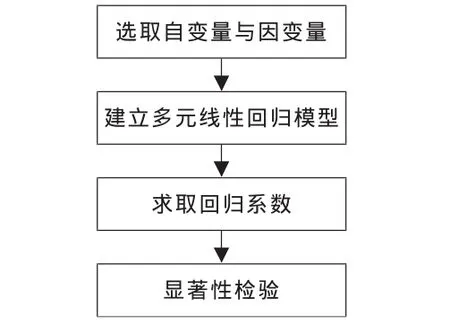
圖1 多元線性回歸分析預測噪聲聲壓級的過程

3.2 建立多元線性回歸模型[9]

在對IEC 61400-11國際標準詳細研究后，選擇了與LAeq有密切關系的幾個物理量作為自變量建立數學模型如下：

設：Y 為 LAeq；X1為輸出電功率；X2為偏航角；X3為溫度；X4為大氣壓力；X5為轉速；X6為槳距角；X7為風向；ε為每次測量時的隨機誤差。

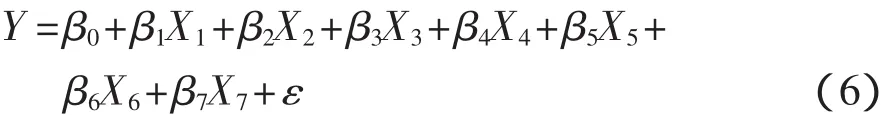
3.3 求取回歸系數

2008年5月，在新疆大阪城風場對某公司的1.5MW風力發電機組在開機狀態下進行聲發射測試，測量得到了噪聲的聲壓、輸出電功率、偏航角等上述模型中所需要的各個物理量，并通過計算得到了風機噪聲的聲壓級LAeq。測試持續35min，共得到210組數據。測試完全按照IEC61400-11標準的要求，具有較高的準確性和可信度。通過以上測得的數據，用最小二乘法求解回歸系數，得到多元線性回歸方程為：

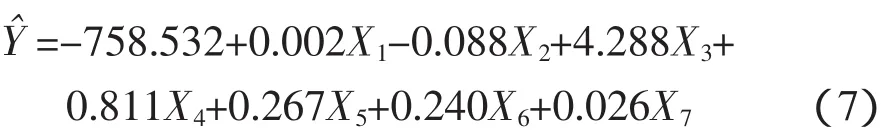
3.4 顯著性檢驗

由于事先并不能確定聲壓級與上述自變量之間具有線性關系，在建立回歸方程之前只是假設它們之間具有確定的線性關系，因而要對所得到的多元線性回歸方程進行顯著性檢驗。下面我們運用F檢驗法，對在3.3中所得到的多元線性回歸方程進行顯著性檢驗。

按照假設檢驗的原理與程序，提出原假設為：

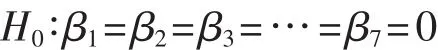
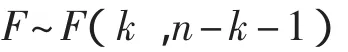
k——變量數，此次檢驗k=7；

n——樣本容量，n=210。

根據變量的樣本觀測值和估計值計算得到F≈70.99。詳細計算結果見表2。

表2 進行顯著性檢驗的結果

給定一個顯著性水平α=0.05，查F分布表，得到一個臨界值Fα=0.05（7，202）≈1.26。于是有F＞Fα=0.05（7，202），所以線性關系在95%的顯著水平下成立。

3.5 計算相對誤差

相對誤差的計算公式為[10]：

計算得到相對誤差的平均值為1.58%，計算結果見圖2，誤差處于可接受范圍內，說明用該多元線性回歸模型對風力發電機組噪聲的聲壓級進行預測是有效可行的。

4 結束語

多元線性回歸分析經常被用來對某些因變量的變化趨勢做出預測。該文給出了風力發電機組聲發射測試過程中對風機噪聲的聲壓級進行預測的多元線性回歸模型，并于2008年5月在新疆大阪城某風場進行了現場實驗。實驗結果表明，運用該模型對風力發電機組噪聲的聲壓級進行預測具有較高的精度和很強的實用價值。

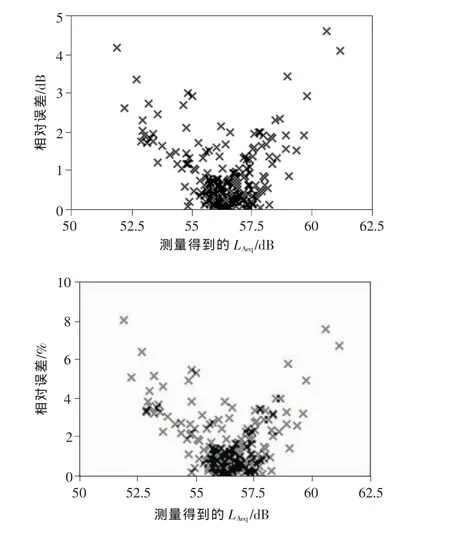
圖2 相對誤差的計算結果

[1]Sun L，Qin SH R，Bo L.Measurement system for wind turbines acoustic noise assessment based on IEC standard and Qin’s model[J].Chinese Journalof Scientific Instruments，2008，29（3）：458-465.

[2] Anon.Turbine noise and the environment[J].Noise Vib Worldwide，2004，35（2）：20-21.

[3]周燕莉.風力發電的現狀與發展趨勢[J].甘肅科技，2008，24（3）：9-11.

[4]International Electrotechnical Commission.IEC 61400-11：Wind turbine generator systems-Part 11：Acoustic noise measurement techniques Ed.2[S].Switzerland：IEC，2006.

[5] 張堯庭.多元統計分析引論[M].北京：科學出版社，1983.

[6] 張堯庭，朱曉冬.隨機向量相關性度量[J].應用概率統計，1988，4（1）：27-34.

[7] 宋來忠，王志明.數學建模與實驗[M].北京：科學出版社，2005.

[8] 謝云蓀，張志讓.數學試驗[M].北京：科學出版社，2000.

[9]陳勝利，郭冬瓊，張 玥.一種油田產量和可采儲量的預測模型及應用[J].承德石油高等專科學校學報，2004（4）：32-35.

[10]秦樹人，張明洪，羅德楊.機械工程測試原理與技術[M].重慶：重慶大學出版社，2002.