一種MASH1-1-1結構∑-Δ調制器設計及應用
潘林杰,王志剛,師奕兵
(電子科技大學自動化工程學院,四川 成都 611731)
1 引 言
隨著無線通信技術的迅速發展,作為核心技術之一的頻率合成技術,其性能和指標如捷變、低相噪、高頻率分辨率等,愈加成為研究的重點[1-2]。在傳統的整數頻率合成器中,輸出頻率是參考頻率的整數倍,頻率分辨率是它的參考頻率。要想提高頻率分辨率就得減小鎖相環的參考頻率,但是減小鎖相環的參考頻率會延長頻率轉換時間,因此整數頻率合成器的頻率分辨率和頻率轉換速度是矛盾的[3-4]。而在小數頻率合成器中,它通過切換多模分頻器的瞬時分頻比N和N+1來實現小數分頻,輸出頻率是參考頻率的分數倍,因此可以在高的參考頻率下得到高的頻率分辨率而不延長頻率的轉換時間。小數頻率合成器雖然解決了整數頻率合成器中頻率分辨率和頻率轉換時間的矛盾,但是它存在的另一個缺陷就是引進了尾數調制(或稱為量化噪聲)問題[5]。
抑制尾數調制的方法有兩種,一種是將瞬時相位誤差按照一定的轉化比例進行D/A變換,通過相加放大器來抵消鑒相器的誤差輸出,該技術稱為模擬相位內插(API)技術。但是由于受到模擬器件水平的限制,內插精度只能達到10-5,而且只有10-3可調范圍,對尾數調制的抑制大約70 dB左右[5]。另一種是采用基于MASH結構的∑-Δ調制技術,它能將小數分頻產生的量化噪聲進行整型,將大部分的量化噪聲能量都被推到頻率高端,只有小部分噪聲能量還留在環路帶寬內,這樣就可以利用鎖相環的模擬低通濾波器濾除小數分頻產生的大部分量化噪聲[6-8]。
2 小數分頻的尾數調制分析
小數分頻鎖相環的一般原理如圖1所示。圖中通過一個包括累加器的控制器,按一定規律周期性地更改分頻比N和N+1來實現小數分頻。設TN表示分頻比為N的時間,TN+1表示分頻比為N+1的時間,則有:
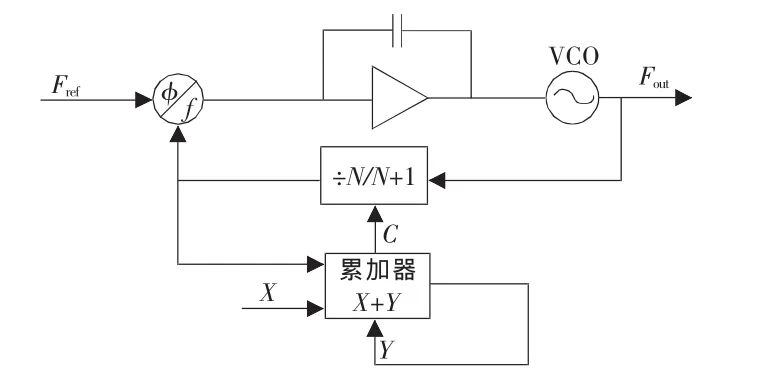
圖1 小數分頻鎖相環一般原理
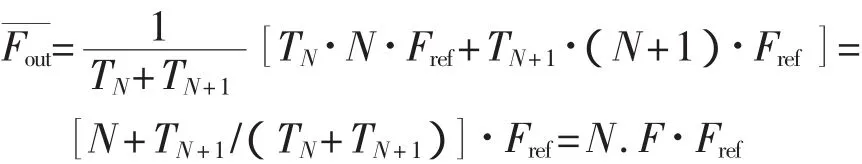
式中:Fref——鎖相環的參考頻率;
N——分頻比的整數部分;
F——分頻比的小數部分。
圖1中,當鎖相環鎖定時,分頻器的分頻比不是固定的,而是在N或N+1之間變化。由于輸出頻率Fout=N.F·Fref,所以當分頻比為N時,鑒相器的輸入信號Fout/N相位比參考頻率Fref相位超前2π.F/N。隨著累加器的不斷累加,兩者的相位差不斷增加,直到累加器溢出后,分頻器的分頻比變為N+1,這時兩者的相位差突然降到0,其結果是鑒相器輸出呈現階梯鋸齒波形,如圖2所示。
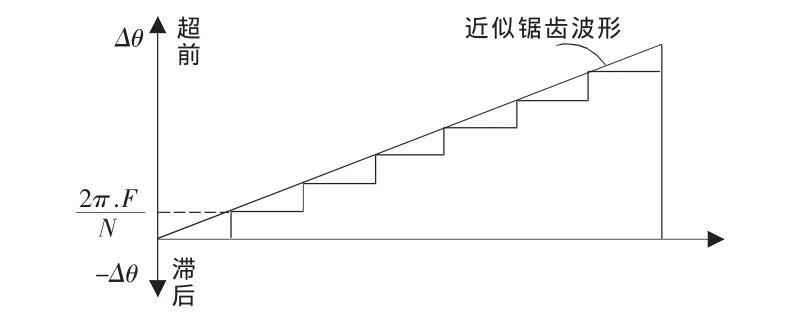
圖2 普通小數鎖相環鑒相器輸出
這樣一個波動的電壓信號加到VCO將會產生頻率調制,調制頻率fm=0.F·Fref,即小數分頻產生尾數調制。由于尾數調制的影響,輸出信號的頻率中除了載波Fout外還有大量Fout±nfm寄生分量,這將嚴重影響VCO輸出信號的質量。
3 MASH1-1-1結構Σ-Δ調制器分析
由上面的討論可知小數鎖相環輸出頻率中包含了大量的雜散和寄生分量,因此需要對小數分頻產生的尾數調制進行有效抑制。抑制尾數調制的方法有兩種,一種是模擬相位內插(API)技術,另一種是采用基于MASH結構的Σ-Δ調制技術。API技術由于受到模擬器件水平的限制,很少被應用。基于MASH結構的Σ-Δ調制技術對小數分頻產生的量化噪聲進行整形,大部分量化噪聲都被推到高頻端,只有小部分留在環路帶寬內,從本質上抑制了小數頻率合成器的尾數調制問題。
該文采用的是基于MASH1-1-1結構Σ-Δ調制器,其結構如圖3所示,由三個一階一位量化器的Σ-Δ調制器組成。與其他結構Σ-Δ調制器相比,其結構更加簡單。要實現這個數字調制器,只需要3個加法器和3個鎖存器,每一個加法器的溢出是一位的0或者1,控制邏輯簡單。
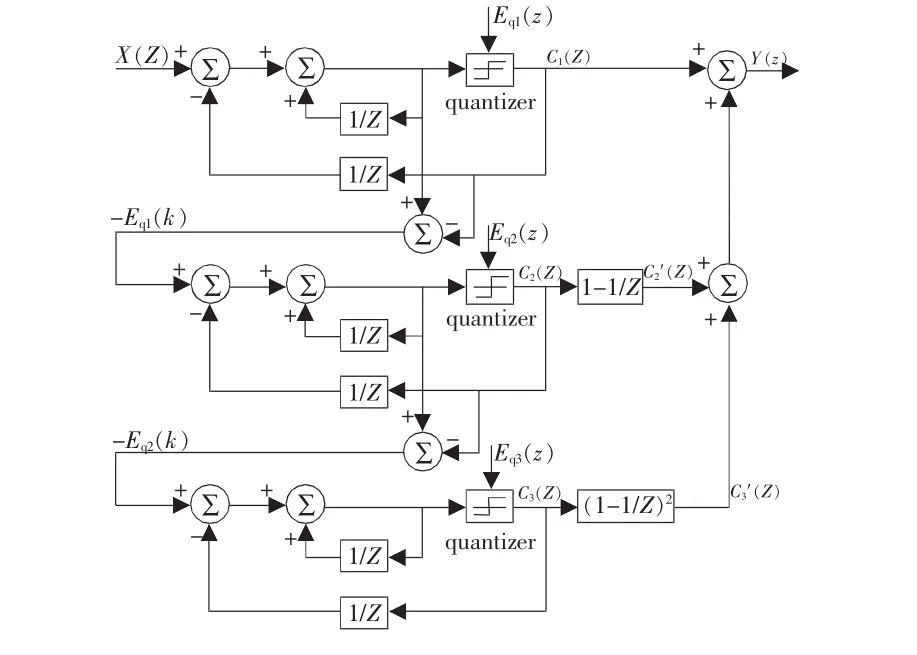
圖3 MASH 1-1-1三階Σ-Δ調制器Z域圖
圖3中C1(Z),C2(Z),C3(Z)分別是各級調制器的累加器溢出信號,Eq1(Z),Eq2(Z),Eq3(Z)是各級的量化噪聲,Z是離散時域中的LaPlace變量,它們的關系式如下所示:
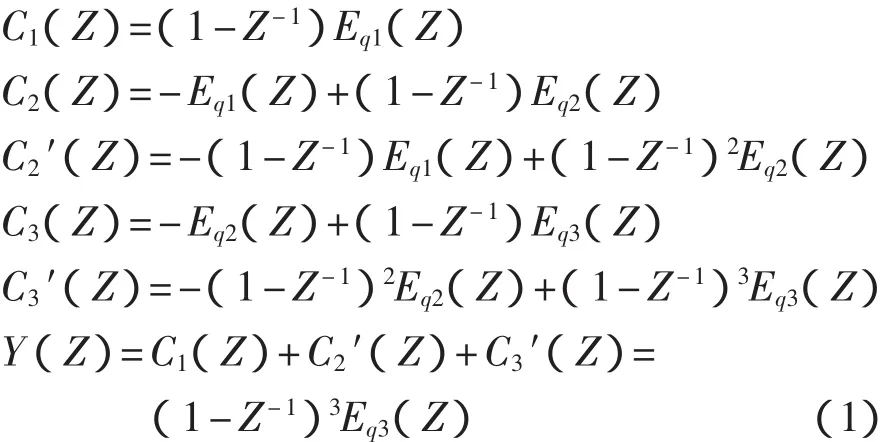
由式(1)可得MASH1-1-1三階Σ-Δ調制器噪聲傳遞函數:
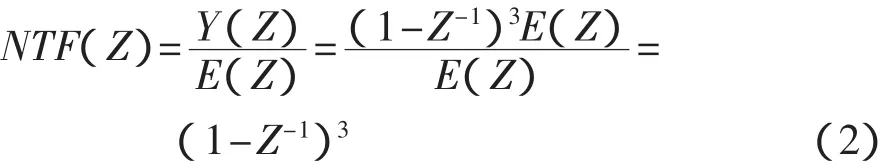
式中:NTF(Z)——三階Σ-Δ調制器噪聲傳遞函數;E(Z)——量化噪聲(由于每級都是相同的一位量化器,它們的量化噪聲都是一樣的,用E(Z)來表示)。
由式(2)可得,MASH1-1-1三階Σ-Δ調制器噪聲傳遞函數NTF(Z)包含3個位于坐標原點的極點,3個位于單位圓上的零點,因此系統是穩定的。
在DC~Fref頻帶內,量化誤差Eq(Z)的方差為1/12,則它的功率譜密度Sq(Z)為1/(12Fref)[5]。設S′q(Z)表示經過MASH1-1-1三階Σ-Δ調制器后的噪聲功率譜密度,則:

式(3)的頻域表達式為:
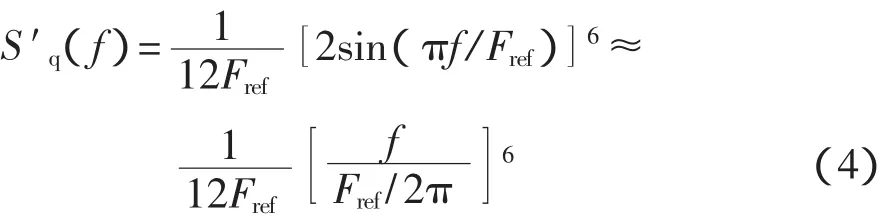
由式(4)可以看出,經過MASH1-1-1三階Σ-Δ調制器后量化噪聲的功率譜密度是頻率f的單調遞增函數,噪聲的能量隨著頻率f的增加呈指數遞增。而當f/Fref很小時,S′q(f)是很小的,幾乎可以忽略。
圖4是經過MASH1-1-1三階Σ-Δ調制器整形后的量化噪聲功率譜密度分布圖,可以明顯看出量化噪聲的能量大部分被推到高頻端,只有小部分留在環路帶寬內。圖4中的歸一化頻率是相對于Fref。
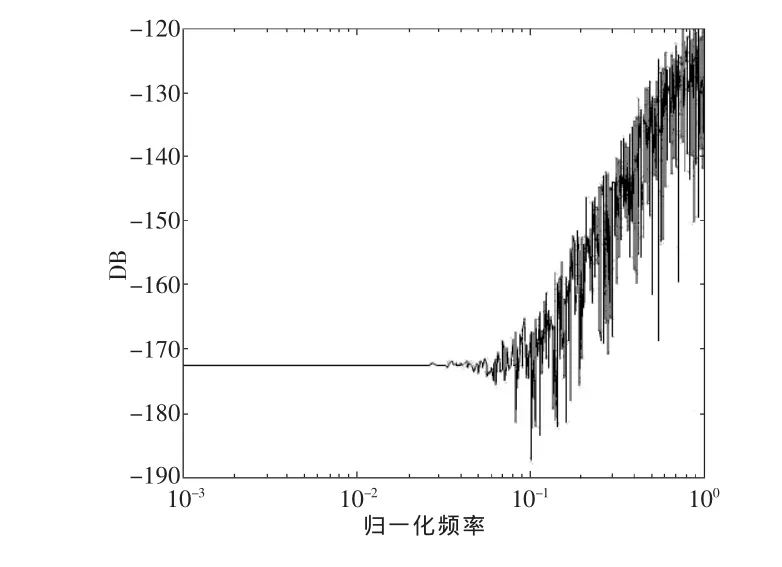
圖4 整形后的量化噪聲功率譜密度分布圖
4 MASH1-1-1結構三階Σ-Δ調制的電路實現
圖5即為上述MASH1-1-1三階Σ-Δ調制器在FPGA中的實現原理圖,24位累加器對應(1-Z-1)-1,D觸發器對應單位時延Z-1,數字加法器對應求和運算。

圖5 MASH 1-1-1三階Σ-Δ調制器實現電路
在圖5電路中,第一級累加器的溢出方式與最簡單的小數分頻的溢出方式相同,在第一級累加器溢出的那一周期,分頻比變為N+1。第一級累加器的余數輸出給第二級累加器進行數字積分,在溢出的那個周期,分頻比變為N+1,延遲一個時鐘周期后分頻比變為N-1。第二級累加器的余數輸出給第三級累加器進行數字積分,在溢出的那個周期,分頻比變為N+1,延遲一個時鐘周期后分頻比變為N-2,延遲兩個時鐘周期后分頻比變為N+1。
在每個調制參考周期內,分頻比Ndiv的變化范圍為N+4~N-3。分頻比經過數字加法器修正后,最終輸出給可編程分頻器。例如N為7’h78(十進制為120),F 為 24’h330201(十進制為 3 342849),輸出的平均分頻比為120.199249339059,其中小數分頻比為:
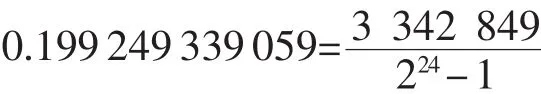
5 結束語
利用Σ-Δ調制技術將小數分頻產生的噪聲能量推到高頻端,然后通過鎖相環的低通濾波器濾除是現代頻率合成器設計的一個發展方向。基于MASH1-1-1結構Σ-Δ調制器具有結構簡單、實現方便、控制邏輯簡單的特點,可廣泛地應用于A/D轉換器和頻率合成器。該文利用FPGA來實現Σ-Δ調制器,可以達到降低功耗、縮小PCB面積、節約成本、設計更加靈活方便的目的。
[1]Chen C Y,Ho J J,Liou W R,et al.A 5.2GHz CMOS fractional-n frequency synthesizer with a MASH deltasigma modulator[C]∥MWSCAS.2008:738-742.
[2] Miller B,Conley R J.A multiple modulator fractional divider[J].IEEE Instrumentation and Measurement,1991,40(3):578-583.
[3]龔 薇,汪道輝.Σ-Δ技術在鎖相環頻率合成器中的應用[J].微計算機信息,2006,22(102):96-98.
[4]唐金元,王翠珍.鎖相環電路在數字電壓表噪聲抑制中的應用[J].計量與測試技術,2008,35(5):6-7,10.
[5] 劉祖深,王積勤.用Σ-Δ調制噪聲成形技術實現小數N頻率合成器的設計討論[J].電子測量與儀器學報,2003,17(4):20-25.
[6] Kratyuk V,Hanumolu P K,Moon U K,et al.A low spur fractional-n frequency synthesizer architecture[C]∥ISCAS.2005(3):2807-2810.
[7]Riley T A D,Copeland M A,Kwasniewski T A.Deltasigma modulation in fractional-n frequency synthesis[J].IEEE Journal of Solid-State Circuits,1993(28):553-559.
[8]Wang H,Brennan P V,Jiang D.FPGA implementation ofsigma-delta modulatorsin fractional-n frequency synthesis[C]∥ISSCS.2007,1(13-14):1-4.

