論物動學中公理化的形數結合幾何學方法（2）

曾煒鋒

（桂林市崇善路灣塘二巷5號2－4－2，廣西 桂林 541002）

本文是文［1］的第一個續篇。

整個自然界是辯證地發生、發展和消亡而過程轉化為再生的，這在至今仍然有效的而以文言秘語著之的中國古典科學中，是有文獻供考而可重新發現的。如：

《老子》（四十八章）：“為學日益，為道日損，損之又損，以至于無為。無為而無不為。”《論衡·遣告》：“夫天道，自然也，無為；如遣告人，是有為，非自然也。”

分，幾何分形——整個自然界的形數結合的幾何學，是有其形式表現的。如：《莊子·天下》：“一尺之捶，日取其半，萬世不竭。”又《天道》：“必分其能”，即必分整個現實宇宙的總能量，亦即設整個現實宇宙的總能量值為形上的常數一而分之。

關于形數結合的幾何分形，《莊子·齊物論》：“有分，有辯。”《系辭傳》（下）：“辯是與非。”《莊子·至樂》：“無為可以定是非。”又《天道》：“故古之人貴夫無為也。”

1 對稱

在科學研究中，對稱這個概念，最初源于日常生活。如人的面部器官（耳目鼻口）以鼻梁為中心左右兩側的正常分布基本相同，就說它是對稱的。《莊子·天下》：“譬如耳目鼻口，皆有所明，不能相通，猶百家眾技也，皆有所長，時有所用。”

關于對稱，理論物理學家楊振寧（1922－）說：“物理學中對稱的概念直接取自我們日常的見解。在動力學問題中，按照對稱來考慮，可以得到重要的結論。”［2］理論物理學家李政道（1926－）表明的見解尤為重要，他說：“1974年5月30日清晨約6點鐘，我住的北京飯店的房間里電話突然響了。我被告知，毛主席打算1 h后，在中南海住處見我。尤其使我感到驚訝的是，見面時他想了解的第一件事竟是物理學中的對稱。”

“根據韋伯斯特詞典，對稱的意思是‘平衡的比例’或者‘產生于平衡的比例的形式美’。”在中文里，對稱有幾乎完全相同的含義。從本質上說，對稱是個靜止的概念。而根據毛澤東的觀點，社會進化的基礎在于變革。動態，而非靜態，才是唯一重要的基本要素。他強烈地感覺到這種認識對于自然界肯定也是對的。所以才奇怪為什么對稱會在物理學中占有那么崇高的地位。

“在我們的會見中，我是唯一的客人。我們的坐椅之間是一個小茶幾。上面放著鉛筆、筆記本和兩杯綠茶。我把鉛筆【筆者按：這鉛筆的幾何學抽象為圖1-a1】放在筆記本上【即圖1-a1是位于一個平面之上】，把筆尖【圖1-a2的‘0’端】指向毛澤東，然后再把筆尖轉向我【圖 1-a3】。鉛筆【圖 1-a2】轉過來【圖1-a3】又轉過去【圖1-a2】。我指出，這運動沒有一刻靜止，但這整個過程卻具有對稱性。毛澤東很欣賞這樣的演示，并且問到對稱的更深含義，問到物理學家能否僅僅根據對稱性原理真正描述出普遍規律”，［3］即真正描述出“質化為量過程轉變為量化為質和質守恒的規律”，［1］亦即真正描述出——宇宙總能量之化為商過程轉變為商化為能和宇宙總能量守恒定律。

但是，李政道教授上述演示唯一的缺失是，未聲明其演示為就地取材——不可彎折的一支鉛筆（圖1-a1）。因為，木質的剛性鉛筆是不能對它施以可塑性實踐，以求得必須的某種經驗知識的。換言之，人們現在已知文［1］中的圖 3-a5或圖 5-a6內的實者表整個現實宇宙，即本文中的圖1′-a1表整個現實宇宙。對圖 1′-a1施以一定形式實踐的對折，則得整個現實宇宙內部的相對運動態（圖 1′-a2）。經驗地繩直圖 1′-a2，則得標量態的圖 1′-a3。將該標量態的圖 1′-a3，變換成矢量態的圖 1′-a4，是可能的。不可否認的事實是，只有在圖 1′-a4這種情況下，李政道教授才有可能以其手執圖1′-a4的中點，令其繞該中點轉過來（圖1′-a5）又轉過去（圖1′-a4）。李政道教授指出，這運動沒有一刻靜止，但這整個過程卻具有對稱性（圖1′-a6）。

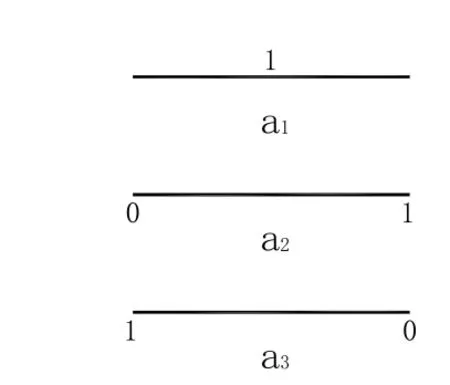
圖1 一支鉛筆及其動向

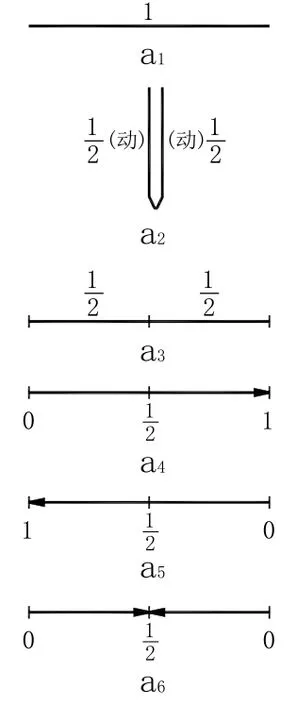
圖1 ′現實宇宙及其對稱

在此，我們用圖1來對應恩格斯、列寧的經典唯物辯證法思想的見解，并非無益。

恩格斯說：“運動【圖1′-a4】應當從它的反面【圖1′-a5】即從靜止【圖1′-a6】找到它的【可求解得的數值無窮小量的】量度，這對于我們的形而上學者【康托爾及其鼓吹者希爾伯特】來說當然是一道【連續統假設（continuum hypothesis）】難題和一付苦藥。”［4］

列寧說：“統一物【圖1′-a1】之分為兩部分【圖1′-a3】以及對它矛盾著【圖1′-a6】的部分【圖1′-a6的右側或左側】的認識，是辯證法的（是辯證法的‘本質’之一，是它的主要特點或特征之一，甚至是它的最主要特點或特征）。”［5］

毛澤東《矛盾論》：“按照唯物辯證法的觀點，自然界的變化，主要地是由于自然界內部矛盾的發展。……唯物辯證法是否排除外部的原因呢？并不排除。唯物辯證法認為外因是變化的條件，內因是變化的根據，外因通過內因而起作用。”

一言以蔽之，經典唯物辯證法的這些重要論述，必定會通過本文于后的形數結合的幾何分形及其可持續發展，而將逐一定量地表現出來。

2 幾何分形

在中國的數學科學史上，最早的幾何分形之學，在老子（公元前571－公元前？）之著《老子》一書中，即《老子》（四十八章）：“為學日益【筆者按：①學，見《說文解字》：“學，篆文敩省。”《書·說命下》：“惟敩，學半。”《說文解字》：“半，物中分也。”②日，見《說文解字》：“日，實也”】，為道日損【①道，見《莊子·繕性》：“道，理也。”理，見《說文解字注·理》：“鄭注樂記曰：理，分也。”②日，見《說文解字》：“日，實也。”③損，見《說文解字》：“損，減也”】，損之又損，以至于無為。無為而無不為。”但是，老子之著《老子》書中，這種以文言秘語而著之的幾何分形之學，今已幾乎無人能識。

《辭海》（1999年版）：“老莊學派以老子、莊子學說為主的道家學派。《史記》以老莊同傳，稱莊子‘其學無所不窺，然其要本歸于老子之言’。”如：

《老子》（四十三章）：“不言‘之’教，無為‘之’益，天下希及‘之’。”《莊子·知北游》：“夫知者不言，言者不知，故圣人行不言‘之’教。”

莊子（公元前369－公元前286）學說，即莊子之著《莊子》。《辭海》（1999年版）：“《莊子》亦稱《南華經》。道家經典之一。莊子及其后學著。《漢書·藝文志》著錄《莊子》52篇，現僅存郭象注本保留下來的33篇。其中內篇七篇，一般認定為莊子著；外篇雜篇可能攙雜有他的門人和后來道家的作品。一說內、外、雜諸篇都反映了莊子的思想。其文章汪洋恣肆，并多采用寓言故事形式，想象豐富。……歷來注解極多，于今通行本有郭象（？－312）注，王先謙（1842－1917）《莊子集解》、郭慶藩《莊子集解》等。”本文中的《莊子》，皆引自王先謙《莊子集解》。

《莊子·天下》：“一尺之捶【筆者按：一，其數；尺，其形。一尺，數與形結合的幾何學的圖形（圖1′）】，日取其半【日、半，見《說文解字》：“日，實也。”又：“半，物中分也”】，萬世不竭”而無為以終。

［定理 2］現實宇宙的總能量，日取其半，取之又取，以至于無為而終。

解：設現實宇宙的總能量值為尺（形）上的常數 1（文［1］中的圖3-a5或圖5-a6上的實者，即本文中的圖1′，亦即圖2-a1－6）。

求證：現實宇宙的總能量值1（圖2-a6），日取其半，取之又取，以至于無為而終。

證：幾何直觀表明，圖2-a6中唯實無虛，是不言而喻的。在中國的古漢語中，所謂日取其半，即實取其半或實取其物中分也。《說文解字》：“日，實也。”又：“半，物中分也。”

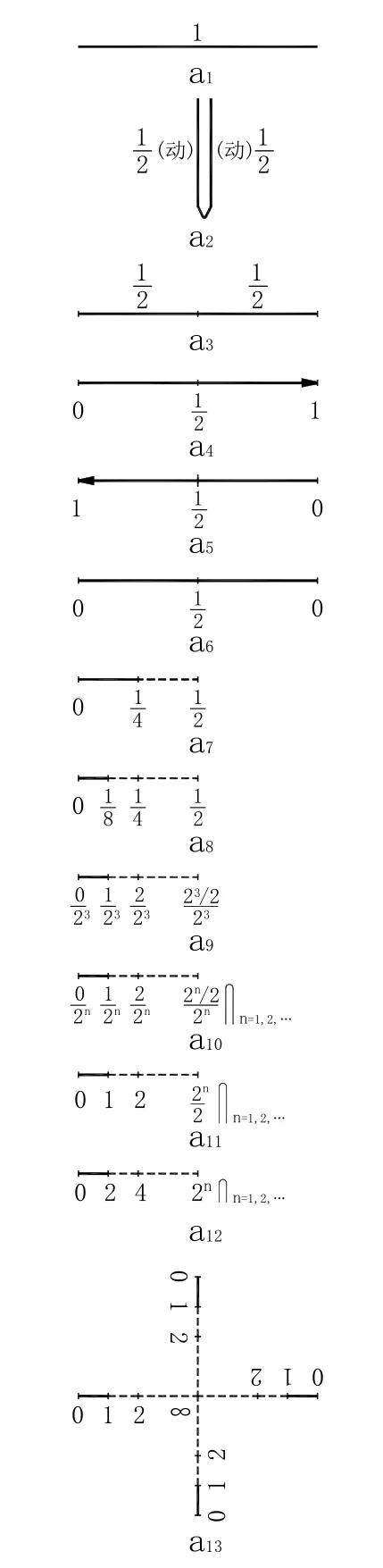
圖2 幾何分形及其張量態

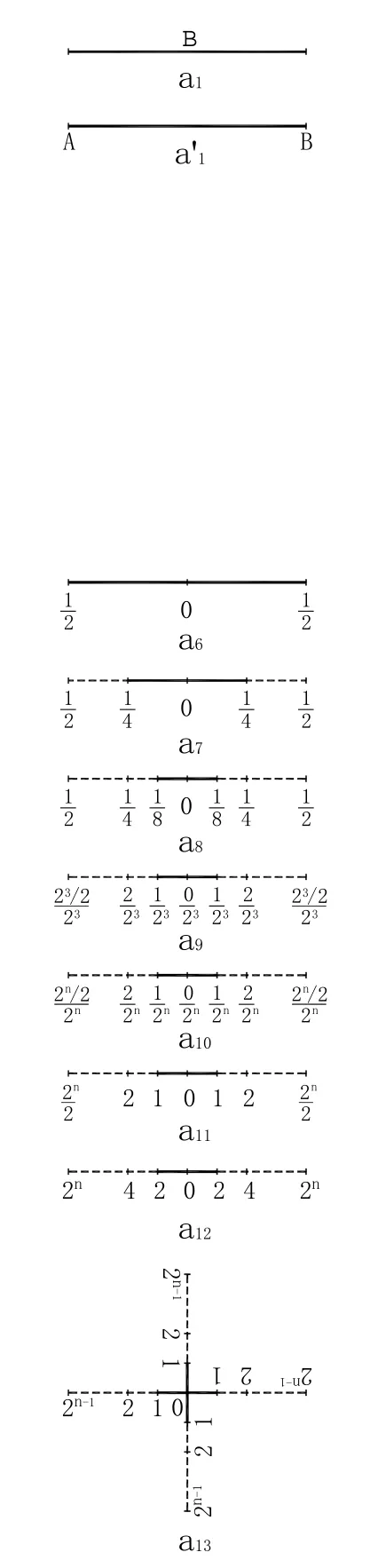
圖2 ′歐氏幾何?平面直角坐標

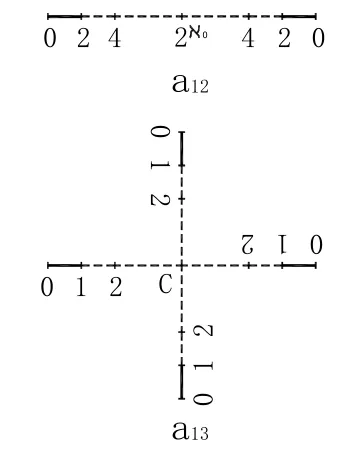
圖2 ″連續統的基數

對圖2-a6實取其半，則得圖2-a7。

對圖2-a7實取其半，則得圖2-a8。

遵《莊子·天運》：“不可多取”之訓導，而對圖2-a8中的分數通分，則得圖2-a9。

將圖2-a9一般化，則得圖2-a10。

以張量描述宇宙膨脹著的整個自然界，即對圖2-a10施以去分母的張量運算，則得圖2-a11。又繼續對圖2-a11施以去分母的張量運算，則得圖2-a12或圖2-a13。

結論：現實宇宙的總能量值1（圖2-a1－6），日取其半（圖2-a7），取之又取（圖2-a8），用至于無為（圖2-a12或圖2-a13）而終。

證畢。

3 幾何微分

什么是科學？孫鉞說：“科學是認識世界的過程。”［6］或者說，科學是定量地認識現實宇宙的過程，尤以幾何微分為工具，而求解得我們人類的宇宙過程極為敏感的初始條件或邊界條件。

哈利韋爾（Jonathan J. Halliwell）說：“量子宇宙學家不可推卸的任務是提出宇宙初始條件或邊界條件的定律。”［7］不幸的是，西方學術界的這種努力，至今仍未見成效。

在中國本土的傳統科學中，自然科學（又稱“量子渾沌宇宙學”），其目的是要求解得量子渾沌宇宙態（圖 2-a12或圖2-a13）。而且，量子渾沌宇宙態是幾何微分的直接基礎，即是隱行別也的直接基礎。《說文解字》：“微，隱行也。”又：“分，別也。”又：“別，分解也。”分解也，即別解也，亦即量子凝聚形式有序宇宙學的初始條件或邊界條件之解也，不可不察。

所謂渾沌，是以其量子——能量子（實）與虛量子（不實）同向相連或未別來表征的。（圖2-a12）《辭海》（1999年版）：“渾沌①同“混沌”。——曹植（192－232）《七啟》：“夫太極之初【筆者按：①夫，見《說文解字》：“夫，——周制以八寸為尺”，即密制以八寸（圖 2″-a12，即圖 2-a12）為尺（圖 1，即圖 2-a1－6）。②之，見《莊子·田子方》：“凡之亡也”】，渾沌未分【即能量子（實）與虛量子（不實）同向相連而未別（圖2-a12）。《說文解字》：“分，別也”】。”又：“混沌①古……天地相連的狀態。《白虎通·天地》：‘混沌相連【筆者按：連（圖2-a12），見《莊子·大宗師》：“連乎其似好閉也。”《易·坤·文言》：“天地閉。”《禮記·月令》：“天地不通閉塞而成冬。”《說文解字注·冬》：“冬之為言終也。”《莊子·田子方》：“凡之亡也”】，視之不見，聽之不聞。’”《中華大辭典》（1915年編）：“混沌，陰陽未分也【筆者按：引伸為虛、實同向相連而未別也】。見《字匯》。”故曰：量子渾沌的數學科學形式表現，即圖2-a12，不誤。

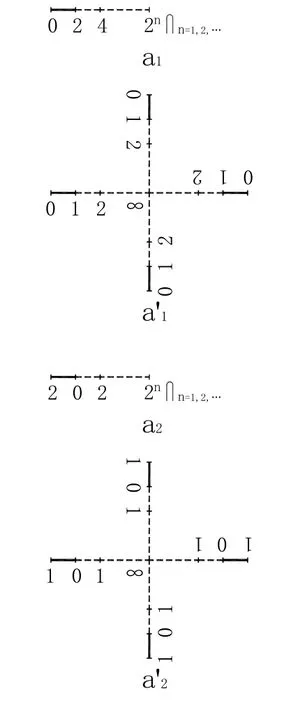
圖3 從渾沌到可迭代有序

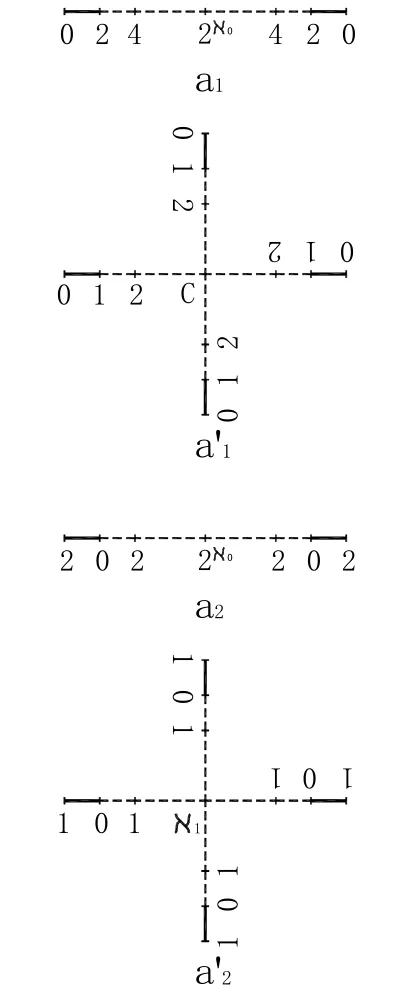
圖3 ′連續統的基數·序數及N1

所謂幾何微分，即《老子》書中至今仍然有效的“無為而無不為”之說，亦即《莊子》書中的“有為”之說。

《老子》（四十八章）：“為學日益，為道日損，損之又損，以至于無為【圖2-a12或圖2-a13，即圖3-a1或圖3-a′1】。無為而無不為【圖3-a2或圖3-a′2】。”《莊子·天道》：“無為也，則用天下而有馀；有為也，則為天下用而不足。故古之人貴夫無為也。”因為，《老子》書中的“無為”，即是幾何分形之終（圖2-a12或圖2-a13）。《莊子·秋水》：“消息盈虛，終【圖2-a12或圖2-a13，即圖 3-a1或圖 3-a′1】則有始【圖 3-a2或圖 3-a′2】。”又《知北游》：“死【圖 2-a12或圖 2-a13，即圖 3-a1或圖 3-a′1】也生之【之，見《莊子·人間世》：“而知‘之’所為‘出’乎哉。”《說文解字》：“之，出也”】始【圖3-a2或圖3-a′2】。”故曰：始【圖3-a2或圖 3-a′2】，即量子凝聚形式有序宇宙階段［1］極為敏感的初始條件或邊界條件，亦即我們人類的宇宙過程極為敏感的初始條件或邊界條件。但是，敏感其何？這個問題于中國古代流傳至今以文言秘語而為之的文獻中，是有記載的。如，

《老子》（四十八章）：“取天下【圖2-a12，即圖3-a1，亦即圖 5-a1。《史記五帝本紀》：“天下謂之渾沌”】常以無事。”《莊子·大宗師》：“無事而生定。”又《逍遙游》：“定乎內、外【圖5-a1，即圖 3-a1，亦即圖 2-a12】之分【圖 5-a2（《說文解字》：“之，出也。”又：“分，別也”），即圖3-a2】。”《禮記·大學》：“外本內末。”又如，

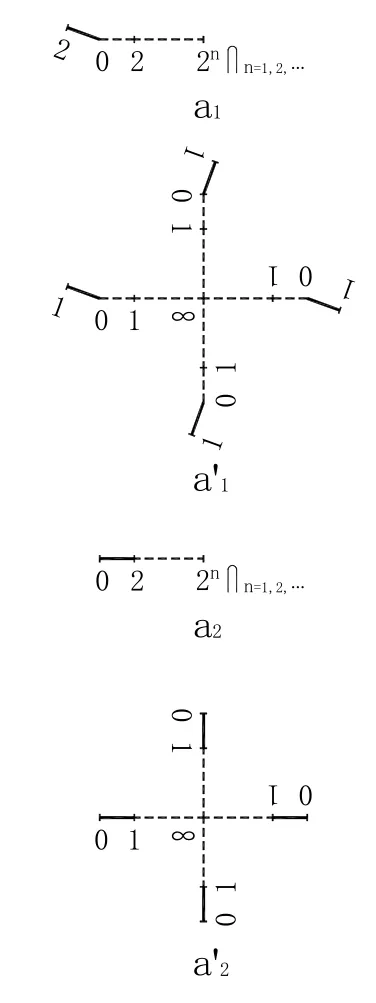
圖4 無窮積分或無窮集合

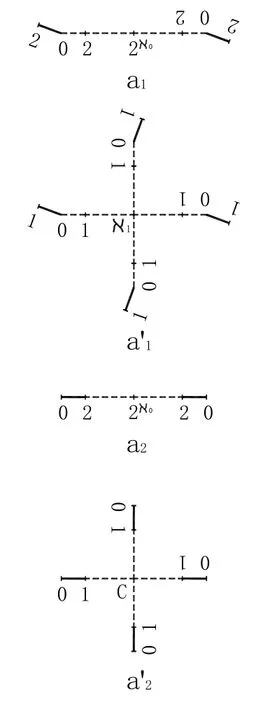
圖4 ′連續統假設

《老子》（四十八章）：“取天下常以無事【1．以，見《說文解字》：“以，用也。”2．無事，見圖 6-a1，即圖 3-a1，亦即圖2-a12】。及其有事【有事，即事至。《莊子·田子方》：“事至而斷”（圖 6-a2，即圖 3-a2）】，不足【圖 6-a2，即圖 3-a2】以取天下【用取圖 6-a1，即圖3-a1，即圖 2-a12】。”《禮記·樂記》：“宮為君，商為臣，角為民，徴為事，羽為物。【筆者按：即圖6-a1為圖 6-a2】”《論語·學而》：“敏于事【圖 6-a2】。”

商（圖6-a1，即圖3-a1，亦即圖2-a12），見《中華大辭典》（1915年編）：“商，張也，陰氣開張。”又：“商，漏刻也。《儀禮士昏禮注》日入三商為昏。《通雅》三商，三刻也”。再見《辭海》（1999年版）：“商④漏刻。古代漏壺中箭上所刻的度數。《儀禮·士昏禮》賈公彥疏：‘鄭目錄云：‘日入三商為昏。’……商，謂商量【曾煒鋒按：商量，讀作Shānɡ liànɡ。［辨誤］在這里，商量——不能讀作 Shānɡ liánɡ】，是漏刻之名。’”再者，《莊子·天下》：“譬如耳目鼻口【筆者按：見圖 7-a1，即圖 3-a1，亦即圖2-a12】，皆有所明，不能相通，猶百家眾技也，皆有所長，時有所用。”又《知北游》：“耳目聰明【筆者按：見圖7-a1，即圖3-a1，亦即圖2-a12】。”又《天地》：“聰明睿知，給數以敏。”《論語·學而》：“敏于事【圖 6-a2，即敏于數 0（圖 7-a2）】。”《系辭傳》（上）：“易，無思也【筆者按：無，見《說文解字》：“無，亡也”】，無為也【無為（圖2-a12，即圖3-a1，亦即圖7-a1），見《莊子·田子方》：“無為而才自然矣。”《論衡·遣告》：“自然也，無為”】，寂然不動【中國的寂然不動說與西方的熱寂說于宇宙過程互相對立。見文［1］的圖7】，感而遂通天下之故。”《禮記·樂記》：“感于物【筆者按：物，見圖 6-a2，即圖 7-a2】而后動【動，見圖7-a3或圖6-a3，即圖4-a1】。”《莊子·刻意》與《莊子·天道》皆曰：“動而與陽同波【圖7-a3，即圖6-a3，亦即圖4-a1或圖4-a′1】”，此即中國古代科學中至今仍有效的量子宇宙波動說。

霍金（Stephen Hawking）在就任［英］劍橋大學盧卡西恩講座教授的就職講演中說：“我認為【我們人類的】宇宙【過程】的初始條件，是和局部的物理定律一樣，都是同樣適合作為科學研究及理論的課題來探討的。”［8］不幸的是，霍金教授及他的西方同行們，事實上至今仍未能“對宇宙的初始條件及局部的物理定律做出解釋。”［8］

其實，量子渾沌宇宙態【圖2-a12，即圖3-a1】的局域等值變換【圖3-a2】，則得我們人類的宇宙過程的極為敏感的初始條件或邊界條件。

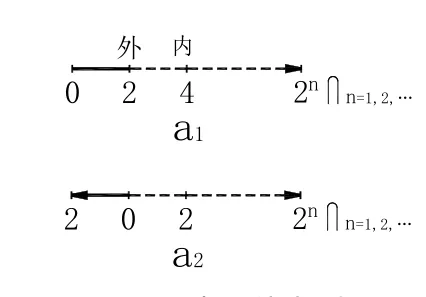
圖5 內、外出別

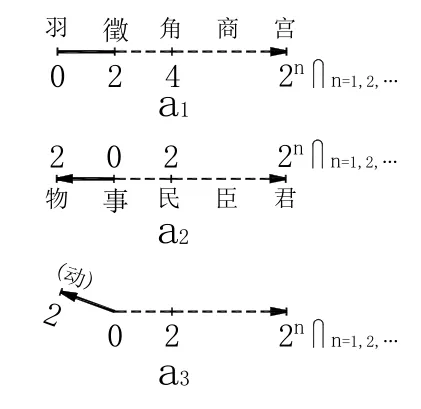
圖6 無事·有事

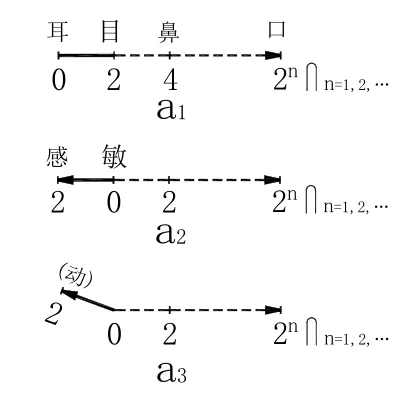
圖7 七竅·敏感·動

4 無窮積分或無窮集合

在中國古代的數學科學中，以道家學派為代表創建的無窮積分或無窮集合，仍是以文言秘語來表述的。所以，道藝復興，是重振中國科學的前提條件。（見表1）

《老子》（四十八章）：“為學日益，為道日損，損之又損，以至于無為【圖2-a12或圖2-a13，即圖3-a1或圖3-a′1】。無為而無不為【圖3-a2或圖3-a′2】。”《莊子·天道》：“無為也，則用天下而有馀；有為也，則為天下用而不足。故古之人貴夫無為也。”《老子》（七十七章）：“有馀者【圖2-a12或圖2-a13，即圖3-a1或圖 3-a′1】，損之 【圖 3-a2或圖 3-a′2】；不足者【圖 3-a2或圖3-a′2】，補之【圖 4-a1或圖 4-a′1及圖 4-a2或圖 4-a′2】。”《莊子·天下》：“以有積為不足【圖3-a2或圖3-a′2】”，即以有無窮積分為圖3-a2或圖3-a′2，亦即有無窮積分極為敏感的初始條件或邊界條件為圖3-a2或圖3-a′2。因為，圖3-a2即圖7-a2是不言而喻的。

再者，《莊子·大宗師》：“陰陽于人【筆者按：人，見《說文解字》：“人，天地之性最貴者也”】。”又《知北游》：“人之【筆者按：之，見《莊子人間世》：“而知‘之’所為‘出’乎哉。”《說文解字》：“之，出也”】生，氣之聚也，聚則為生，散則為死。”又：“死【圖 2-a12或圖 2-a13，即圖 3-a1或圖 3-a′1】也生之始【圖3-a2或圖3-a′2】。”又《人間世》：“氣也者，虛而待物【圖6-a2，即圖3-a2中以同步迭代】者也【圖6-a3，即圖4-a1】。唯道集虛【筆者按：1．唯，見《辭海》（1999年版）：“唯④語助詞，無義。《論語·述而》：‘與其進也，不與其退也，唯何甚。’”2．道，何謂道？《系辭傳（上）》：“一陰一陽之謂道”，其形數結合的幾何學語言即：一陰一陽出謂道（圖6-a2，即圖3-a2），《說文解字》：“之，出也。”3．集，見《左傳·襄公二十六年》：“今日之事，幸而集。”（1）事，見《莊子·田子方》：“事至而斷”（圖6-a2）。（2）幸，見《莊子·德充符》：“幸能正生”，即幸能是生（圖3-a2）。《說文解字》：“正，是也。”再見《中華大字典》（1915年編）：“幸本作。《說文夭部》：“吉而免兇也。從，從夭。夭，死之事，死謂不。《段注》死為不幸，則免死為幸。”筆者：死（圖2-a12，即圖3-a1）為不幸，則免死（圖3-a2，即圖6-a2）為幸。故曰：所謂幸而集，即圖3-a2而集。《辭海》（1999年版）：“集⑥通‘輯’。輯睦；……”輯睦，見《左傳·成公十六年》：“輯睦以事君”，即輯睦用事君（圖6-a2，即圖 3-a2）。《說文解字》：“以，用也。”4．集虛，即無窮集合和無限程序的有限多個同步迭代步驟有其完整解，因為圖6-a2即圖3-a2中存在著的迭代者與被迭代者之間的可整除關系是其根據。”】。”這就是我們重新發現《莊子》書中以文言秘語而為之且至今仍有效的，無窮集合之說及其解。

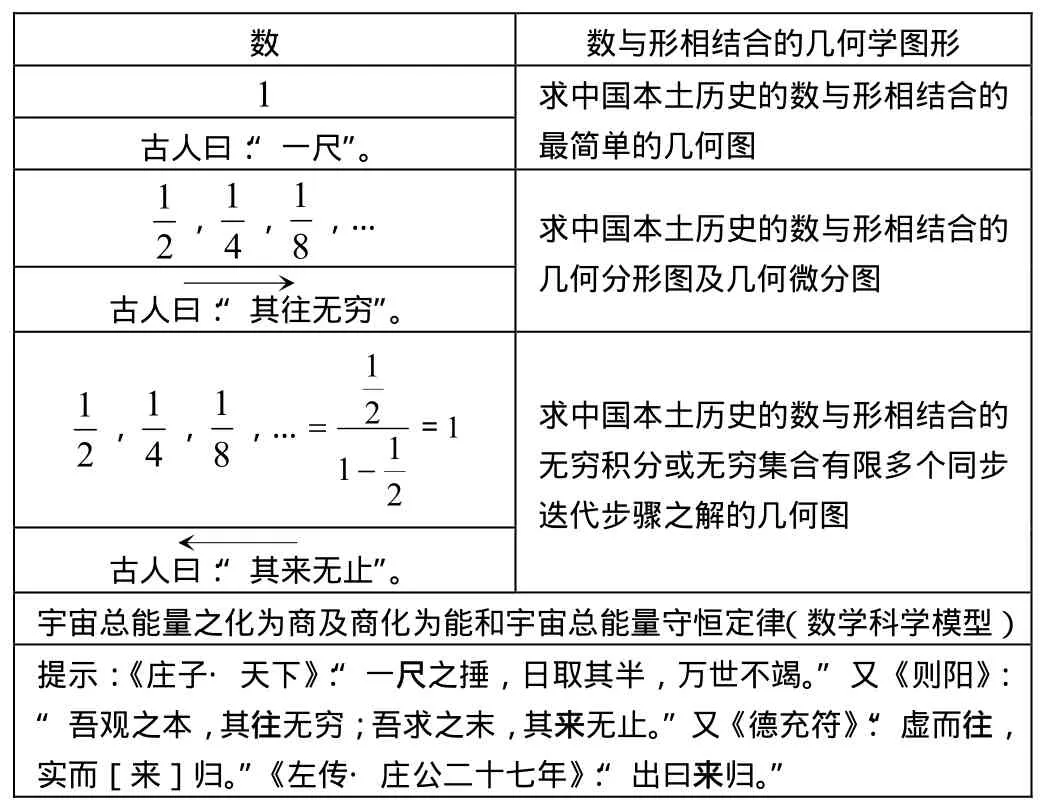
表1 中國古代的數學科學

5 西方的數學

什么是西方的數學的全貌？

數學家張恭慶教授說：“由于數學的壯大和發展，20世紀以來，已經沒有一個人能夠像龐加萊（Henri Poincaré，1854－1912）和希爾伯特（David Hilbert，1862－1943）當年那樣通曉數學的全貌了。”［9］

式(24)雖然消除了輔助參數但θ2中卻同時引入了另外的輔助參數ρ.顯然，θ2中ρ和x,y是相關的，因此式(24)的結果同樣并非最優.為此，在第3步中，利用θ2中輔助參數ρ與目標位置x,y的約束關系來構建方程，從而進一步提高目標位置的估計精度.考慮的估計誤差，則由ρ=x2+y2可得：

所以，我們僅限于簡要地逐一討論與本文相關的、西方的歷史的數學中的一些問題。

5.1 歐幾里得《幾何原本》

愛因斯坦（Albert Einstein，1879－1955）說道：“西方的科學發展是以兩個偉大的成就為基礎，那就是：希臘哲學家發明形式邏輯體系（在歐幾里的幾何學中），以及（在文藝復興時期）發現通過系統的實驗可能找出因果關系。在我看來，中國的賢哲沒有走上這兩步，那是用不著驚奇的。要是這些發現果然都作出了，那倒是令人驚奇的事。”［10］

關于歐幾里的幾何學，西方的數學史權威莫里斯·克萊因（Morris Kline，1908－1992）說：“Euclid的直線是我們所說的線段。”［11］

我們的初級中學課本《幾何》中說道：“線段用表示它的兩個端點的兩個大寫字母來表示【筆者按：即本文中的圖2′-a′1】，也可以用一個小寫字母來表示【即本文中的圖2′-a1】。”［12］

張英伯教授說：“歐幾里得《幾何原本》中的內容已在現代中等教育中分成了若干部分，分別歸入平面幾何、代數、三角、立體幾何。初中平面幾何的內容主要取材于《幾何原本》的前六章，……。《幾何原本》的開頭列出的5個公理和五個公設……公理適用于數學的各個領域……公設適用于幾何部分。”［13］

M·克萊因說：希臘“古典時期【初等】數學成就的精華是 Euclid的《原本》。”［11］“作圖題在希臘幾何中起重要作用，而Euclid公設確實限制只許用尺規作圖。【張理京、張錦炎譯注：“‘尺規’兩字是按習慣說法譯的，這里的‘尺’實際應是‘直邊’，理應理解為沒有刻度的尺。”】”［11］他還指出：“Euclid舉出如下的公設：

（1）從任一點到任一點作直線［是可能的］。

（2）把有限直線不斷循直線延長［是可能的］。

（3）以任一點為中心和任意距離［為半徑］作一圓［是可能的］。

（4）所有直角彼此相等。

（5）若一直線與兩直線相交，且若同側所交兩內角之和小于兩直角，則兩直線無限延長后必相交于該側的一點。”稍后，M·克萊因說：“頭3個公理說的是可以構作線和圓。所以它們是對兩件東西存在性的聲明，在第一篇里的講述過程中，Euclid通過構作證明了其他一些東西的存在，但平面是例外。”［11］

筆者警覺到，M·克萊因教授的上述說教，對人們具有極大的欺騙作用。

首先，歐幾里得《幾何原本》的公設1，從任一點到（另）任一點作直線。

眾所周知，歐幾里得幾何作圖，必須有其作圖用的工具和給定的已知的作圖條件，這樣就會出現如下兩種可能的情況：

一種可能是，若事先給定作圖的工具——一把沒有刻度的直尺和一個圓規（《辭海》（1999年版）：“圓規作圖用的作圖工具。有兩股，上端鉸接，下端可隨意分開或合攏，以調整所作圓或圓弧半徑的大小”），則歐幾里得《幾何原本》的公設1是作不成圖的。因為，作圖用的作圖工具——尺長已定，若給出的任意兩點間的距離大于作圖工具——尺長，則作不成圖。若給出的任意兩點間的距離小于作圖工具——尺長，而作出的直線（線段）其對應于作圖工具——直尺上至少有一刻度，而與歐幾里得《幾何原本》的作圖工具——無刻度的直尺之規定相悖。

另一方面，若先給定任意的兩點，并以此兩點間的距離為準，去制造一把長度相對應而無刻度的直尺，然后以該直尺為作圖的一定工具，對上述給定的任意兩點間作直線（線段）雖為可能，但是這種作圖是沒有普適性的。

所以，歐幾里得《幾何原本》的公設 1，是其尺規作圖規定作不成圖的一個所謂假設。

再者，歐幾里得《幾何原本》公設 2，即把有限直線不斷循直線延長；公設5，即平行公設或平行公理。

關于歐幾里得《幾何原本》的這兩條公設或公理，甚至西方的數學史權威M·克萊因也指出道：“關于在物質空間里是否可假定存在無限直線這個與此【平行公理】有關的問題，起初沒有那么多人關心，但終于突出成為【與平行公理】同樣重要的問題。Euclid只是小心地假設，可以按需要延長一條（有限）直線，因而甚至那延長后的直線也還是有限的。還有Euclid敘述平行公理的特別措辭，說兩條直線將在截線的同旁內角之和小于兩直角的一側相交，這是為了避免直接說出兩條直線無論怎樣延長都不相交的一種方式。然而，Euclid確實含有無限直線存在的思想，因為假若直線都是有限的，則在任何情況下它們也不能按需要任意延長，而且它證明了平行線的存在性。”［14］

其三，歐幾里得《幾何原本》的公設 3，以任意一點為圓心和任一距離（為半徑）可作一圓。

筆者斷言，所謂“以任意一點為圓心和任一距離（為半徑）作一圓”，是不可能的。因為，歐幾里得《幾何原本》的作圖工具之一為無刻度的直尺，其尺長已經給定，則其另一作圖工具——圓規，其規距能夠也只能夠作以該直尺的尺長為半徑的圓。換言之，歐氏《幾何原本》作圖工具之一——無刻度的直尺的尺長一定，則其另一作圖工具——圓規是而且只能夠是一個死規或銹規，即規距既不能夠大于也不能夠小于直尺的尺長，亦即規距是也只能夠是恒為尺長的圓規。

結論：綜上所述，歐幾里得《幾何原本》的所謂出發點——公理體系，不真。

5.2 坐標幾何或解析幾何

關于坐標幾何，M·克萊因說：“Fermat和Descartes是數學中【繼 Euclid《幾何原本》之后】下一個巨大創造的主要負責人，……他們所創立的科目叫坐標幾何或解析幾何，其中心思想是把代數方程和曲線曲面等聯系起來。這個創造是數學中最豐富最有效的設想之一。”［15］

雖然，M·克萊因吹捧了坐標幾何，他還是不得不指出道：“別的數學家用比較粗魯的語言攻擊分析方法。Carnot希望‘把幾何學從分析學的畫符樣難懂的文字中解放出來。’這個世紀后期，Eduard Study（1862－1922）稱坐標幾何的機器似的過程為‘坐標磨坊的嘎嘎聲。’”他還接著說：“對幾何學解析方法的反對不只是出于個人的偏好或口味。首先，一個真正的問題是，到底解析幾何學是不是幾何學？因為方法和結果的實質都是代數，它們的幾何意義都是隱蔽的。”［14］

對解析幾何的見解，數學家張恭慶教授的見解尤為離譜，他說：“數學一開始就是研究‘數’和‘形’的。從古希臘時期起，人們就已試圖把它們統一起來。目的雖未能完全達到，但卻找到了兩者之間的種種聯系，推動了數學的發展。17世紀笛卡爾的解析幾何可謂是這兩者結合的典范，用‘數’研究‘形’，引進了坐標，也引進了變量數學。”［9］

《辭海》（1999年版）：“坐標，確定平面上或空間中一點位置的一組有序數。例如，在平面上，取點O為原點，過點O引互相垂直的兩條直線 X′OX、Y′OY，稱為坐標軸，從一點P作它們的垂線 PM、PN。設從點 O到垂足M和N的距離是|X|和|Y|，視垂足M在點O的右或左，N在點O的上或下，而規定X和Y的正和負。稱（X，Y）為點P在笛卡兒坐標系XOY下的坐標，簡稱‘直角坐標’。”

事實上，人們歷來不知“平面直角坐標”的真正來歷唯本文中的圖2′，即反科學或背離科學的圖2′。

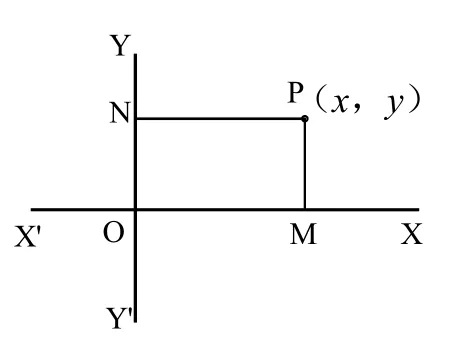
圖8 平面直角坐標

5.3 集論——無窮集合和無限程序

關于西方的數學，M·克萊因說：“二十世紀數學中最為深入的活動，是關于基礎的探討。強加于數學家的問題，以及他們自愿承擔的問題，不僅牽涉到數學的本性，也牽涉到【西方的】演繹數學的正確性。”［16］

論及西方的數學基礎，M·克萊因指出：“1930年以后的全部發展還留下來兩個沒有解決的大問題：去證明不加限制的經典分析與集合論的相容性，以及在嚴格【幾何】直觀的基礎上去【重新】建立【西方的】數學，或者去確定這種途徑的限度。在這兩個問題中，困難的根源都在于無窮集合和無限程序中所用到的無窮（infinity）。”［16］

關于集合論，M·克萊因說：“西方的集合論的創建者是Georg Cantor（1845－1918）。”［16］他又說：“Contor指出，他的關于無窮數或超限數的理論，不同于普通所說的一個變量變得無窮小或無窮大的那個無窮的概念。兩個一一對應的集合具有相同的勢或基數。對于有限集合來說，基數就是這集合中的元素的個數。對于無窮的集合，要引進新的基數。自然數集合的基數用N0表示。”［16］他還說：“Cantor已經證明，對于給定的任一集合，總可以構造一個新的集合，即所給集合的所有子集構成的集合，使其基數大于所給集合的基數。如果給定集合的基數是N0，則其全部子集構成的集合具有基數2No。Cantor已經證明2No＝C，這個C就是連續統的基數。另一方面，他通過序數引進了N1，并證明N1是N0的后繼者，于是N1≤C。

至于N1＝C是否成立，即連續統假設（continuum hypothesis）是否成立，Contor不管怎樣刻苦努力，也不能回答。在1900年的國際數學會議上，Hilbert把這個問題列入了著名問題的名單中。”［16］

但是，西方的數學中的康托爾連續統假設欲獲證明，其于中國的傳統數學科學中不過是順手牽羊的小事一樁。如，

5.4 從混沌到有序

在中國的古典數學科學中，從渾沌到有序的最簡要的文言秘語表述是，《莊子·在宥》：“渾渾沌沌，終身不離【筆者按：所謂終身不離，即死亦相連——連續統（圖2-a12或圖2-a13，即圖3-a1或圖3-a′1）或大一統。《公羊傳·隱公元年》：“何言乎王正月？大一統也。”《莊子·天下》：“歷物之意，曰：至大‘無’外，謂之大一；至小‘無’內，謂之小一。”1．無，見《說文解字》：“無，亡也。”2．內、外，見《禮記·大學》：“外本內末”（圖5-a1，即圖2-a12）】；若彼知‘之’【之，見《莊子·田子方》：“凡之亡也”（圖2-a12，即圖3-a1）】，乃是離‘之’【之，見《莊子·人間世》：“而知‘之’所為‘出’乎哉。”《說文解字》：“之，出也”（圖 3-a2，即圖 5-a2）】。”

本文于前已引《辭海》（1999年版）：“老莊學派以老子、莊子學說為主的道家學派。《史記》以老莊同傳，稱莊子‘其學無所不窺，然其要本歸于老子之言’。”如：

《莊子·在宥》：“渾渾沌沌，終身不離；若彼知之，乃是離之”一說，然其要本歸于老子之言——《老子》（四十八章）：“為學日益，為道日損，損之又損，以至于無為【圖2-a12，即圖3-a1】。無為而無不為【圖3-a2，即圖5-a2】。”

但是，西方的理論物理學家海森堡（Werner Karl Heisenberg，1901－1976）問道：“二千五百年以來，哲學家和自然科學家一直在討論這個問題：如果人們試圖把物質一次又一次地不斷分割下去，將出現什么情況？什么是物質的最小成分？”［17］另一方面，西方的數學家哈爾莫斯（P. R. Halmos）說：“渾沌（chaos）概念與動力系統概念有關，粗略地講，混沌理論研究動力系統的無窮過程的行為。……渾沌通常與分形（fractal）有關。”［18］

一言以蔽之，西方的物理學家和數學家，至今仍無人能知從渾沌到有序的定量之解，即使是伊里亞·普里戈金（Ilya Prigogine，1917－2003）亦不例外。曾慶宏（1941－）和沈小峰（1934－）說：“《從混沌到有序》（Order out of chaos）是比利時著名科學家、諾貝爾獎金獲得者伊·普里戈金教授和他的學生、同事伊·斯唐熱（Isabelle Stengers）博士合寫的一本關于自然科學哲學問題的著作。”［19］

5.5 三體問題

在人類的科學史上，所謂三體問題，是可積系統的形式表現問題，即《老子》（七十七）章：“不足者（圖3-a2或圖3-a′2）”的形式表現問題，亦即《莊子·天下》：“以有積為不足（圖3-a2或圖 3-a′2）”之說。

另一方面，M·克萊因說：“三體運動問題成為New ton以來的【西方的】一個主要問題，至今還未解決。”［15］又：“在三體問題中得到一些特殊精確解，是拉格朗日（Joseph Louis Lagrange，1736－1831）在1772年一篇得獎論文《論三體問題》中給出的。這些解中，有一個是說，這些物體能夠作這樣的運動，使得它們的軌道是同時描出的3個相似橢圓，而且以三物體的質量中心為其共同的焦點。另一個是，假定3個物體從一個等邊三角形的3個頂點開始運動，那么它們就好象粘住在這個三角形上運動著，而這個三角形本身圍繞著三物體的質量中心轉動。第三個是，假定三物體是從一直線上的初始位置投入運動的，那么在適當的初始條件下，它們將繼續固定在這一直線上，而這條直線在一平面上圍繞物體的質量中心轉動。對于Lagrange來說，這3種情況是沒有物理實在性的，然而那個等邊三角形的情況在1906年被發現適用于太陽、木星和一個名叫Achilles的小游星。”［15］普里戈金說：“一個受到非常廣泛研究的例子就是三體問題，這或許是動力學史上最重要的問題。既受地球又受太陽影響的月球的運動，就是這個問題的一例。人們作了無數次嘗試去把它表述成一個可積系統的形式，直到十九世紀末，布倫斯（Bruns）和彭加勒證明了這是不可能的。”［19］

顯然，既受地球又受太陽影響的月球的運動，是天體物理中的問題。林家翹教授指出：“宇宙論和天體物理是不同的兩種學科。”［20］其實，可積的三體問題的對象，是也只是整個宇宙——我們人類的宇宙過程的初始條件或邊界條件，即中國古代的“以有積為不足【圖3-a2】”（《莊子·天下》）。

5.6 地圖四色問題

西方的法朗西斯·古特里（Francis Guthric）于1852年提出了一道數學難題——地圖的四色問題（亦稱“四色猜想”）。所謂地圖的四色問題，是指能否只用四種顏色在地圖上把所有的地區涂色，使相鄰的兩個地區的顏色不同。

歐陽光中指出道：“1976年9月，《美國數學會通告》宣布了一件震撼全球數學界的消息：美國伊利諾斯大學的兩位教授阿佩爾（K. I. Appel）和哈肯（W. Haken）……利用電子計算機證明了地圖的四色猜測是正確的。”［21］數學家哈爾莫斯（P. R.Halmos）認為阿佩爾和哈肯聲稱利用電子計算機證明了地圖的四色猜想，是數學進展中的一個突破（explosion），他說：“突破意味著一種大的響聲，一則出乎意料的通告，但不一定是件好事情。”［22］

歐陽光中說：“1977年12月9日我國著名科學家錢學森教授在《人民日報》上發表了一篇題為《現代科學技術》的文章，其中有這樣一段話：‘去年數學界轟動一時的一件事，是用電子計算機證明了數學上的四色定理。畫地圖最多只需要四種顏色。要證明這個定理很難，數學家經過上百年的努力，證明不了。去年美國數學家用電子計算機證明了。他們看到這個問題要證明并不是不可能，而是證明的步驟、程序很復雜，人一輩子的時間也證不完。他們就把程序編好，交給高速的電子計算機去干。高速電子計算機也用了一千多個小時才證出來。美國數學家認為，他們的主要貢獻不在證明了四色定理，而在運用電子計算機完成了這件人沒有能夠完成的事。’”他還接著說：“利用高速電子計算機終于解決了數學中的這一大難題。然而數學家們仍舊在問：證明能否簡化？是否不用計算機也能證明？這些正等待有志者去攻關。”［21］

在筆者看來，意欲證明地圖的四色問題，首先必須畫出地圖，然后方能為其著色。

地圖，見《管子·七法》：“兵也者【筆者按：兵，見《莊子·列御寇》：“兵為外”（圖 5-a1，即圖 2-a12）】，善于地圖【1．地，見《白虎通·爵》：“父天母地，故稱天地。”《莊子·達生》：“天地者，萬物之父母也，合則成體，散則成始。”《禮記·樂記》：“天高地下，萬物散殊。”《莊子·秋水》：“天在內”（圖5-a1，即圖8-a1，亦即圖2-a12）。2．圖，見《老子》（六十三章）：“圖難于其易。”《系辭傳（上）》：“易，無思也［筆者：無，見《說文解字》：“無，亡也”］，無為也。感而遂通天下之故。”《莊子·列御寇》：“知道易，勿言難。知而不言，所以之天也。”又《秋水》：“天在內”（圖5-a1，即圖8-a1，亦即圖2-a12）。《禮記·樂記》：“天高地下”（圖8-a1，即圖2-a12）。《史記·五帝本紀》：“天下謂之渾沌”（圖2-a12）。《周禮·夏官·職方氏》：“掌天下之圖，以掌天下之地（圖 8-a1，即圖 2-a12，亦即圖 3-a1）。”《說文解字》：“圖，畫、計難也”（圖 2-a12，即圖 3-a1）】，謀十官【1．謀，見《莊子·應帝王》：“無為謀府。”又《德充符》：“府萬物。”2．十，見《說文解字》：“十，數之具也。—為東、西，|為南、北，則四方中央備矣”（圖 2-a13，即圖 3-a′1）。3．官，見《中華大字典》（1915年編）：“官，管也。”《禮記王制疏》：“其諸侯以下及三公至士，總而言之，皆謂之官。官者管也”】。”

為地圖（圖 8-a1，即圖 2-a12，亦即圖 3-a1）著色見《莊子·齊物論》：“四者熟知天下之正色哉【筆者按：1．四，見《中華大字典》（1915年編）：“四，陰數也。象四分之形。見《說文四部》。《段注》口像四方，八像分也。”2．天下，見《史記·五帝本紀》：“天下謂之渾沌”（圖2-a12，即圖3-a1）。3．正，見《說文解字》：“正，是也”】。”又《盜跖》：“則變容易色稱不足【筆者按：不足，見《老子》（七十七章）：“有馀者（圖2-a12，即圖3-a1），損之（圖 3-a2）；不足者（圖 3-a2），補之（圖 4-a1及圖 4-a2）。”】”。

所以，在中國的傳統數學科學中，所謂的地圖四色問題，即為圖8-a1涂色問題，亦即為圖2-a12涂色的問題。而另一方面，在西方的傳統數學中，所謂的地圖四色問題，即為康托爾的2No（由圖2-a12牽出的圖2″-a12）涂色的問題。但是，美國的阿佩爾教授和哈肯教授為康托爾的2No配圖了嗎？或者說，他倆怎么會證明了四色猜想呢？

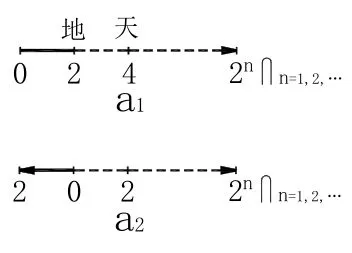
圖8 天高地下

5.7 第一推動

關于“第一推動”之說的由來，方勵之說：“——‘第一推動’是個很老的問題，在亞里士多德的《物理學》中就已提到了。中世紀的托馬斯·阿奎那，則把‘第一推動’作為證明上帝存在的第一種方法。他在《神學大全》中曾如下寫道：

‘在世界上，有些事物是在運動著，這在我們的感覺上是明白的，也是確實的，凡事物運動，總是受其他事物推動。……’

‘如果一件事物本身在動，而又必受其他事物推動，那么其他事物又必定受另一其他事物推動。但我們在此決不能一個一個地推到無限。……所以，最后追到有一個不受其他事物推動的第一推動者，這是必然的。每個人都知道，這第一推動者就是上帝。’

現代科學興起后，許多神學論斷都被科學直接證明是不對的。可是‘第一推動’一直是個難點。牛頓曾表述過大體與阿奎那相同的論斷，也承認存在‘第一推動者’。后來的物理學雖然不再提‘第一推動者’，但也并未回答‘第一推動’是由何推動的。”［23］

宇宙自所謂不動到始動，西方的物理學不解地謂之第一推動。那么，宇宙是怎樣自所謂不動到始動的呢？為了科學定量定態地解答這個問題，不妨重復本文于前已述。即

《老子》（四十八章）：“為學日益，為道日損，損之又損，以至于無為【圖2-a12，即圖3-a1，亦即圖7-a1】。”《論衡·遣告》：“自然也，無為。”《系辭傳》（上）：“無為也，寂然不動。”

《老子》（四十八章）：“為學日益，為道日損，損之又損，以至于無為。無為而無不為【圖3-a2，即圖7-a2】。”《莊子·天道》：“無為也，則用天下而有馀；有為也，則為天下用而不足。故古之人貴夫無為也。”《老子》（七十七章）：“有馀者【圖2-a12，即圖3-a1或亦即圖7-a1】，損之【圖3-a2，即圖7-a2】。”

《老子》（四十八章）：“為學日益，為道日損，損之又損，以至于無為。無為而無不為。”《莊子·天道》：“無為也，則用天下而有馀；有為也，則為天下用而不足。故古之人貴夫無為也。”《老子》（七十七章）：“有馀者，損之；不足者【圖3-a2，即圖7-a2】，補之【圖4-a1及圖4-a2。其圖4-a1，即圖7-a3】。”

文［1］已證，宇宙三過程循環無限有其向下和向上的分枝，而且是宇宙三過程循環無限及其任一過程皆三階段發展的。我們人類的宇宙過程的前身，即非我們人類的宇宙過程的第三階段（向下的分枝過程的第三階段），被《老子》（四十八章）：“為學日益，為道日損，損之又損，以至于無為”（圖2）求解得，且求解得其終——“無為”為圖2-a12，即圖3-a1，亦即圖7-a1的所謂不動態（《系辭傳》（上）：“無為也，寂然不動”）。

所以，宇宙自所謂不動（圖2-a12，即圖3-a1，亦即圖7-a1），而到始（圖3-a2，即圖7-a2）動（圖4-a1，即圖7-a3），根本不存在西方的物理學中的所為“第一推動者”。

1 曾煒鋒.論物動學中公理化的形數結合幾何學方法（1）［J］.科學之友，2009.11（33）：1～6

2 楊振寧.基本粒子發現史（楊振玉、范世藩譯）［M］.上海：上海科學技術出版社，1963.9：52

3 毛澤東同李政道討論“對稱”［N］.人民日報，1988.09.11：第8版

4 恩格斯.反杜林論（中譯本）［M］.北京：人民出版社，1970：59

5 列 寧.談談辯證法問題（中譯本）［M］.北京：人民出版社，1973：1

6 孫 鉞.科學的意義［N］.科學時報，2008.09.18：B3版

7 Jonathan J. Halliwell.量子宇宙和宇宙創生（龔 靜、韓王榮譯）［J］.世界科學，1992.10：4

8 Stephen Hawking.理論物理的盡頭是否已經在望？（林華清譯）［J］.世界科學，1991.7：1、6

9 張恭慶.國際數學家大會和我們［J］.數學通報，2000.7：2、1

10 許良英等編譯.愛因斯坦文集（第一卷）［M］.北京：商務印書館，1976：574

11 M·克萊因.古今數學思想（第一冊）（張理京、張錦炎譯）［M］.上海：上海科學技術出版社，1979：68、31、44、69

12 人民教育出版社數學室編.初級中學課本《幾何》（第一冊）［M］.北京：人民教育出版社，1983：4

13 張英伯.歐氏幾何的公理體系和我國平面幾何課本的歷史演變［J］.數學通報，2006.1：4～5

14 M·克萊因.古今數學思想（第三冊）（北京大學數學系數學史翻譯組譯）［M］.上海：上海科學技術出版社，1980：277～278、245

15 M·克萊因.古今數學思想（第二冊）（北京大學數學系數學史翻譯組譯）［M］.上海：上海科學技術出版社，1979：1、80、228～229

16 M·克萊因.古今數學思想（第四冊）（北京大學數學系數學史翻譯組譯）［M］.上海：上海科學技術出版社，1981：289、323～324、60、66、69～70

17 W. Heisenberg.基本粒子是什么？（范岱年譯）［A］.現代物理學參考資料（第三集）［C］.北京：科學出版社，1978：5

18 P. R. Halmos.數學的進展減慢了嗎？（上）（劉華杰譯）［J］.世界科學，1991.11：12

19 伊·普里戈金、伊·斯唐熱.從渾沌到有序（曾慶宏、沈小峰譯）［M］.上海：上海譯文出版社，1987：1，112

20 陳奎寧.林家翹教授談中國學者的治學方法有可改進之處［J］.大自然探索（自然科學），1984.1：1

21 歐陽光中.地圖四色問題［M］.北京：人民教育出版社，1981：4～5、5

22 P. R. Halmos.數學的進展減慢了嗎？（下）（劉華杰譯）［J］.世界科學，1991.12：5

23 方勵之.宇宙的創生［J］.中國社會科學院研究生院學報，1985.4：4