貝葉斯計量經濟學及面板數據中的貝葉斯推斷

李小勝

（安徽財經大學 統計系，安徽 蚌埠 233030）

0 引言

隨著貝葉斯理論的發展和計算機模擬等數值計算技術的提高，貝葉斯技術已大量應用在各門科學當中，而把貝葉斯理論應用到計量經濟學，是上世紀60年代以來在一大批統計學家和計量經濟學家的共同努力下，迅速發展起來的。貝葉斯計量經濟學的發展主要得益于60年代的Jacques Dréze,Tom Rothenberg,Walter Fisher,Albert Ando,Gordon Kaufman,Arnold Zellner等人。其中 Zellner的《An Introduction to Bayesian Analysis in Econometrics》一書的出版標志著貝葉斯計量經濟學的真正誕生。該書較為全面地闡述了貝葉斯計量經濟學的大多數專題。

隨后出版的大多數計量經濟學的教科書也都含有貝葉斯計量經濟學的章或節，例如Maddala（1978），Intriligator（1978），Malinvaud（1980），Judge et al（1985），Chow(1983)的計量經濟學教課書。相比60年代以前人們應用的非貝葉斯計量經濟學的方法，這個方面的文獻和書籍多了起來。Zellner(1985)對貝葉斯計量經濟學理論發展進行了回顧，秦朵（Qin,1996）從另一個角度也進行了回顧。Poirier,D.J.（2006）更是對國外（1970～2000）幾種重要的期刊使用貝葉斯方法在經濟和計量經濟學文章中的數量的發展速度進行了回顧。當代許多杰出的計量經濟學家如Geweke,Litterman,Dempster,Sims,Maddala,Chib等都應用貝葉斯計量經濟學。華人計量經濟學家秦朵（1994）就應用貝葉斯計量經濟學，李宏毅（1997）把貝葉斯計量經濟學應用到面板數據分析當中。周國富（1990）把貝葉斯計量經濟學應用到資產定價和資產組合中。而國內研究貝葉斯理論的人員很多，但是研究貝葉斯計量經濟學的文獻并不是很多，只有朱慧明（2006）研究了貝葉斯計量經濟學的幾個重要專題，并深入地進行了討論。本文將首先比較經典學派與貝葉斯學派的異同；然后，給出面板數據中應用貝葉斯方法的一些優勢與結果。

1 貝葉斯學派與經典學派之間的差異及其分析的優點

貝葉斯學派與經典學派之間主要差異是明顯的。首先，兩個學派的核心差別是對于概率的不同定義。經典學派認為概率可以用頻率來進行解釋，估計和假設檢驗可以通過重復抽樣來加以實現。而貝葉斯學派認為概率是一種信念。結合這種信念加以假設檢驗（先驗機會比），當數據出現以后就產生后驗機會比。這種方法結合了先驗和樣本信息輔助假設檢驗。其次，兩者差異體現在使用信息不同，經典學派使用了總體信息和樣本信息，總體信息即總體分布或總體所屬分布族的信息，樣本信息即抽取樣本(數據)提供給我們的信息。而貝葉斯學派除利用上述兩種信息外，還利用了一種先驗信息，即總體分布中未知參數的分布信息。兩者在使用樣本信息也有差異，經典統計對某個參數的估計θ^說是無偏的，其實是利用了所有可能的樣本信息，貝葉斯學派只關心出現了的樣本的信息。而且貝葉斯學派將未知參數看作是一個隨機變量，用分布來刻劃，即抽樣之前就有有關參數問題的一些信息，先驗信息主要來自經驗和歷史資料。而經典統計把樣本看成是來自具有一定概率分布的總體，所研究的對象還是總體，而不局限于數據本身，將未知參數看作常量。

貝葉斯分析方法的優點也很多，與頻率方法比較貝葉斯方法充分利用了樣本信息和參數的先驗信息，在進行參數估計時，通常貝葉斯估計量具有更小的方差或平方誤差，能夠得到更精確的預測結果；貝葉斯HPD（最大后驗）置信區間比不考慮參數先驗信息的頻率置信區間短；貝葉斯方法能對假設檢驗或估計問題所做出的判斷結果進行量化評價，而不是頻率統計理論中的接受，拒絕的簡單判斷；在基于無失效數據的分析工作，貝葉斯統計有著重要優點（韓明，2005），一批產品中抽出10進行檢驗，若無不合格品時，經典統計認為次品率為0而貝葉斯統計得到的是1/12，可見貝葉斯估計更謹慎。

2 面板數據的貝葉斯推斷

面板數據是用來描述一個總體中給定樣本在一段時間內的情況，并對樣本中每一個樣本單元都進行多重觀察。這樣的數據在計量經濟學中稱為Panel Data，而統計學中稱為Longitudinal Data。面板數據常用雙下標變量表示。例如

yit,i=1,2,…,N;t=1,2,…,T

N表示面板數據中含有N個個體。T表示時間序列的最大長度。若固定t不變，yi.,(i=1,2,…,N)是橫截面上的N個隨機變量；若固定i不變，y.t,(t=1,2,…,T)是縱剖面上的一個時間序列（個體）。 Mundlak（1961）、Balestra 和 Nerlove（1966）最早把Panel Data引入到經濟計量中。從此以后，大量關于Panel Data的分析方法、研究文章如雨后春筍般出現在經濟學、管理學、社會學、心理學等領域。面板數據分析的文章可謂是浩如煙海，Baltagi與Hisao各自的書中都進行了回顧。

而上面的文章和書籍中的面板數據分析都是在頻率學派的觀點下闡述的，但是把Bayes方法融入面板數據的文章不是很多，且大多數文章只給出了在二次損失函數下的貝葉斯后驗的均值和后驗方差，并沒有給出怎么得來的。本文就用貝葉斯方法來分析面板數據看其優勢所在。面板數據的模型常用下式表示：

yit=ait+xitβit+εit（i=1,2……N；t=1,2,……T）

其中，Xit=(x1it,x2it，xkit)'是 k×1 的外生變量向量；βit=(β1it,β2it，βkit) 是 k×1 的參數向量；ait是截距項，k 為解釋變量的個數ε；εit是k×1的誤差擾動項（標量）。下標it表示第i個單位（個人、家庭、公司和國家等）在第t期的情況。

通常我們的假定是截距項和斜率項不隨時間變化，而且斜率項通常又假定是不變的，截距項隨個體不同而不同。有式：yit=ai+Xitβ+εit。 上式我們可以用一個向量來表示：y=Xβ+ε。其中我們假設ε～N（0，Ω），那么這個面板數據模型的y服從均值為Xβ，方差為Ω的正態分布y～N(Xβ,Ω)。在Ω已知的條件下我們可以應用廣義最小二乘法的均值和方差的估計量，分別為：

β^=(X'Ω-1X)-1X'Ω-1y，Var(β^)=(X'Ω-1X)-1

由于ε到y的雅可比變換是一一對應的變換，所以似然函數為：

f(y|β，Ω)=（2π）-NT/2|Ω|-1/2exp{-(1/2)(y-Xβ)'Ω-1(y-Xβ)}

記 L(β，Ω)=（2π）-NT/2|Ω|-1/2exp{-(1/2)(y-Xβ)'Ω-1(y-Xβ)}=(2π)-NT/2|Ω|-1/2exp{-(1/2)(y-Xβ^)'Ω-1(y-Xβ^)+(β-β^)1X'Ω-1X(β-β^)}

由于：(y-Xβ)'Ω-1(y-Xβ)=(y-Xβ^)'Ω-1(y-Xβ^)+(β-β^)1X'Ω-1X(β-β^)，貝葉斯分析中上述這個模型的先驗假設大致可以分為四種：①已知 Ω 而 β 未知，我們假設 β 服從 π(β|Ω)～N（β0，Ω0）；②Ω和β都未知，我們假設其服從模糊先驗（Jeffreys先驗）分布為：π(Ω)∝|Ω|-（p+1）/2；③已知 β 而 Ω 未知，我們假設其服從 π(Ω)～IWp(n,Ω0)，IW 表示逆 Wishart分布。 維度為 p，自由度為n，Ω0為已知陣，又叫超參數；④Ω和β都未知，我們假設其服從共軛先驗分布為：π(β|Ω)∝π(β|Ω)π(Ω)，即 π(Ω)服從逆Wishart分布，π(β|Ω)表示給定Ω下的正態分布。本文只討論第一種情況，第二種情況得到的后驗估計與廣義最小二乘法相同。第三種一般很少出現，方差信息都已知而參數還未知，一般不用。第四種情況由于超參數太多，一般只有理論上探討的意義。所以若我們取β的先驗分布為β～N(β0，H)，那么先驗密度函數為：

π(β)=（2π）-K/2|H|-1/2exp{-(1/2)(β-β0)'H-1(β-β0)

根據貝葉斯定理。后驗密度似然函數先驗密度。即π(β|y)=π(β)Lπ(β，Ω)。 有：

π(β|y)∝exp{-(1/2)[(β-β^)'X'Ω-1X(β-β^)+(β-β0)'H-1(β-β0)]}

上面的公式中我們已略去與β無關的項，[……]中可以表示為：

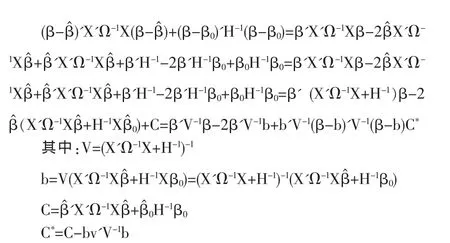
C*中不含有 β，那么最終后驗密度為：π(β|y)∝exp{-(1/2)(β-b)'V-1(β-b)]}，即 β～N(b,V)，在二次損失函數下后驗均值就是關于后驗分布的期望值：

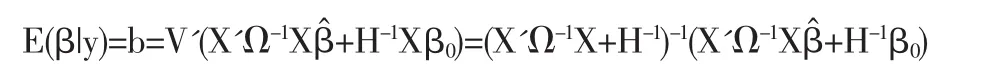
后驗方差為：var(β|y)=V=(X'Ω-1X+H-1)-1

3 結論

從上面的均值和方差可以看出，面板數據的貝葉斯計量經濟學的后驗均值是廣義最小二乘法和先驗均值的加權，后驗方差是先驗方差和樣本方差的加權；貝葉斯方法得到的均值和方差綜合了先驗信息、樣本信息，使推斷更為科學合理。

正如Zellner(1997）所說：在計量經濟學中，經典學派不用先驗信息是很難讓讓人相信的，他們常在想誤差項是個什么分布，有無自相關，建立怎樣的模型（是參數的，還是非參數模型），選擇一個什么樣的顯著性水平，檢驗的勢如何？例如經典學派在假設隨機系數模型和時變參數模型，那么他們對參數分布作出的假定就相當于貝葉斯學派，給出參數的具體分布一樣。當然貝葉斯學派的先驗信息有時也是有很大局限性的，受個人知識和經驗的影響，先驗分布選擇的帶人為的主觀性等，這也是經典學派不用貝葉斯方法的原因。總之，從上述分析可以看出，如果貝葉斯方法使用的恰當會使推斷更為精確。

[1]劉樂平,袁衛.現代Bayes方法在精算中的應用及展望[J].統計研究，2002，(2).

[2]茆詩松.貝葉斯統計[M].北京：中國統計出版社，1999.

[3](美)普雷斯(S.James Press).貝葉斯統計學：原理、模型及應用[M].廖文等譯.北京：中國統計出版社，1992.

[4]朱慧明，韓玉啟.貝葉斯多元統計推斷理論[M].北京：科學出版社，2006.

[5]方開泰.實用多元統計分析[M].上海：華東師范大學出版社，1989.

[6]韓明.基于無失效數據的可靠性參數估計[M].北京：中國統計出版社，2005.

[7]Balestra,P.,M.Nerlove.Pooling Cross-Section and Time-Series Data in the Estimation of a Dynamic Economic Model:The Demand for Natural Gas[J].Econometric,1966，34.

[8]Mundlak,Y.Empirical Productions Free of Management Bias[J].Journal of Farm Economics,1961，(43).

[9]Zellner,A.An Introduction to Bayesian Inference in Econometrics[M].Chichester：John&Wiley，1971.

[10]Press，J.S.Applied Multivariate Analysis:Using Bayesian and Frequentist Methods of Inference[M].Nelbourne：Krieger Publishing，1982.