廣義矩方法及其在金融領域的應用
柳會珍,張成虎,周宗澤
(1.西安交通大學 應用經濟學博士后流動站,西安 710061;2.西安交通大學 經濟與金融學院,西安 710061;3.山西省張峰水庫建設管理局,太原 030012)
0 引言
常用的統計估計方法有矩估計法、極大似然估計法、貝葉斯方法和最小二乘法,在這幾種方法中,極大似然估計和貝葉斯方法需要總體的概率分布,在實際應用中有較大的局限性而且對模型較為敏感;最小二乘法要求模型的隨機誤差項和解釋變量不相關,因而在處理特殊模型時適用,應用范圍較窄。矩估計法是一種簡單的統計估計方法,在參數估計中,只需求出和參數有關的矩,并以樣本矩代替相應的總體矩,組建一個以參數為未知數的方程組,求解方程組得到參數的矩估計。矩估計不受總體概率分布的限制且不需要實際樣本數據的產生過程,因而在實際中得到廣泛應用。總體分布中的一個參數可能和多個總體矩有關,由矩估計法對參數進行統計估計就有可能得到多種估計結果,該采用哪種矩估計,這些矩條件之間關系如何協調,哪個矩條件較為重要,這些問題傳統的矩估計均無法處理。
本文主要介紹廣義矩估計方法的統計思想,對該方法和極大似然估計、最小二乘估計法之間的關系進行了論證研究,同時在數據產生過程具有相關性的條件下對權重矩陣的選取和具體實施過程進行了深入分析,最后給出在金融資產定價方面的應用實例。
1 廣義矩方法的統計性質
1.1 統計思想
假設Xt是一個t期觀察到的(n×1)隨機向量,θ是未知(a×1)參數向量,h(θ,Xt)是(r×1)向量值函數,即 h:Ra×Rn→Rr,滿足E(h(θ,Xt))=0,等式中的r行稱為正交條件或矩條件。
廣義矩方法的統計思想是選取θ使得樣本矩g(θ;YT)盡可能接近零總體矩,即廣義矩估計θ^使得目標函數Q(θ;YT)=g'(θ;YT)WTg(θ;YT)在θ^達到最小,這里 WT是正定權重矩陣, 根據實際應用中不同矩條件的重要性選取。
取 WT為單位矩陣,則目標函數 Q(θ;YT)=g'(θ;YT)g(θ;YT),顯然 Q(θ;YT)≥0,取θ^使 Q(θ^;YT)=0,即 g(θ^;YT)=0,則θ^是參數 θ的矩估計,所以廣義矩估計是矩估計的推廣。
1.2 和最小二乘估計以及極大似然估計的關系
考慮多元線性回歸模型:

其中Xt=(Xt1,Xt2,…,Xtp)'是t時刻觀測到的解釋變量向量,β=(β1,β2,…,βp)'是未知參數向量。
在經濟和金融領域,常假設解釋變量矩陣Xt和隨機誤差 εt不相關,即 E(Xtεt)=0。 由模型(1)可得這個等式就是廣義矩估計法中的正交條件,其中包含p個方程。由于正交條件個數等于待估參數個數p,權重矩陣WT可以取為單位陣,則由廣義矩估計的統計方法可知β))的樣本矩解得參數向量β的廣義矩估計為顯然等于普通最小二乘估計,所以普通最小二乘估計是廣義矩估計的一個特例。
設Zt是一個t時刻觀察到的變量構成的(n×1)隨機向量,zt是隨機向量 Zt的具體觀測值,Zt=(Z1,Z2,…,Zt)表示直到 t時刻所有觀察數據。在給定Zt-1的條件下的Zt條件密度為f(zt|Zt-1,θ),θ是未知參數向量。由密度性質可得:1,A其中表示隨機向量Zt的所有可能取值集合。假設微分和積分順序可交換,兩邊對參數θ求導得即,令,則有E(h(θ,Zt)|Zt-1)=0,顯然正交條件的個數和未知參數個數相同,由廣義矩估計法可得:參數θ的廣義矩估計滿足等式(θ,zt)=0。
將直到T時刻為止觀察到的所有樣本數據構造似然函數得 L(θ;z1,…,zT)=,對數似然為 lnL(θ;z1,…,zT)=假設函數 f(zt|Zt-1,θ)關于 θ 可微,且最大值在參數空間內部取得,則對數似然函數最大化的一階條件為顯然參數向量θ的極大似然估計和廣義矩估計相同,所以在密度函數滿足一定的條件下,廣義矩估計和極大似然估計是一致的。
1.3 權重矩陣的選取
廣義矩估計方法中權重矩陣的選取非常重要,直接決定了正交條件的重要性,即樣本矩接近零的關注程度,所以在利用廣義矩方法對模型參數進行統計估計時,需要考慮實際問題所需,同時為了后續的模型過度識別檢驗工作需要,又要照顧到統計分析處理的有效性。
理論上為了保證廣義矩估計的漸進有效性,選取的逆矩陣作為權重矩陣,這里是過程的{h(θ0,Xt)}的協方差矩陣,其中 Γi=E(h(θ0,Xt)h'(θ0,Xt)),θ0是參數向量的真實值,這里假設h(θ,Xt)過程是平穩的。
1.4 模型過度識別限制的檢驗
2 在金融領域的應用
廣義矩方法在金融資產定價方面有著重要的應用。Cochrane給出的資產定價公式為:pt=Etmt+1(b)xt+1,其中mt+1(b)是隨機折現因子,其中包含了金融資產價格的風險調整因素,b是未知參數向量,xt+1,pt分別是收益向量和價格向量,Et表示已知時刻t時信息下的條件期望[12]。利用期望迭代定律可得:

由于金融資產價格一般變化較大,不具有平穩性,因此為了統計分析處理的方便,我們將公式(2)改寫成收益率形式如下:

公式(3)就是廣義矩方法中的正交條件。令ut(b)=mt+1(b)Rt+1-1,gT(b)=ET[ut(b)]其中記號ET表示樣本均值,則ut(b)是定價誤差,gT(b)是定價誤差的樣本均值。由廣義矩方法要求使gT(b)盡可能接近零總體矩,根據不同的金融資產定價誤差要求,選取權重矩陣WT,使得Q(b;xT)=gT'(b)WTgT(b)達到最小,求得參數向量b的廣義矩估計b^。在金融實證分析中,目標函數Q(b;xT)的最小化可以轉化為求參數向量b的廣義矩估計,滿足等式
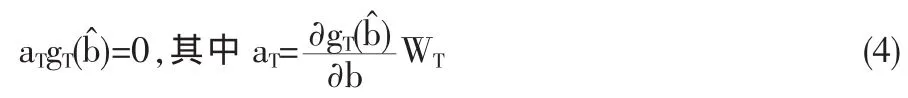
等式(4)表示定價誤差的線性組合為零,即定價誤差向量和一些特殊向量正交,這些特殊向量取決于權重矩陣WT,需要根據實際問題中對各種資產定價誤差的關注程度和統計有效性來確定。
由于金融市場的復雜性,金融資產收益率之間存在一定的相關性,而且個別資產收益率變化較大,在選取權重矩陣時均需考慮這些情形,否則得到的廣義矩估計不能反映真實的定價誤差。
相應的樣本均值為
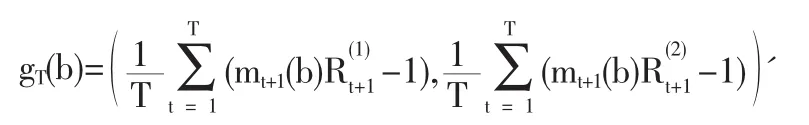
3 總結
由于廣義矩估計不需要像傳統的極大似然估計和貝葉斯估計那樣要求嚴格的分布假設,更適合復雜的經濟和金融系統的參數估計和模型檢驗,因而近年來在計量經濟和金融研究領域得到了廣泛的應用,并且隨著應用的逐步深入進一步推動了廣義矩理論和方法的發展。隨著經濟發展和金融市場的不斷創新,將會出現越來越多的非線性性問題和預測要求,在這些情形下,勢必需要最優化、對模型非線性限制的過度識別檢驗等方法技術,廣義矩理論方法能夠很好地處理這些模型中的參數估計和檢驗問題,因而在計量經濟學和金融領域將有更廣闊的應用前景。
[1]Hansen,L.P.Large Sample Properties of Generalized Method of Moments Estimators[J].Econometrica,1982,50.
[2]Hansen,L.P.,Scott,F.R.The Role of Conditioning Information in Deducing Testable Restrictions Implied by Dynamic Asset Pricing Models[J].Econometrica,1987,55.
[3]Hansen,L.P.,John H.,Erzo,L.Econometric Evaluation of Asset Pricing Models[J].The Review of Financial Studies,1995,8.
[4]Hansen,L.P.,Ravi J.Assessing Specification Errors In Stochastic Discount Factor Models[J].Journal of Finance,1997,52.
[5]Campbell,J.Y.,Lo,A.W.,Mackinlay,A.C.The Econometrics of Financial Markets[M].Princeton:Princeton University Press,1997.
[6]Poon,S.,Rockinger,M,Tawn,J.Extreme-Value Dependence in Financial Markets:Diagnostics[J].Models and Financial Implications.Review of Financial Studies,2003,17(2).
[7]Stock,J.H.,J.H.Wright.GMM with Weak Identification[J].Econometrica,2000,68.
[8]Lars Korsholm.The GMM Estimator Versus Semiparametric Efficient Score Estimator under Conditional Moments Restrictions[C].Working Paper,AarhusSchoolofBusiness,University Aarhus,1999.
[9]詹姆斯D.漢密爾頓,劉明志譯.時間序列分析[M].北京:中國社會科學出版社,1999.
[10]Hansen,L.P.Generalized Method of Moments Estimation:A Time Series Perspective[J].InternationalEncyclopedia ofSocial And Behavioral Sciences,2000,6.
[11]Hansen,B.E.,West K.D.Generalized Method of Moments and Macroeconomics[J].Journal of Business and Economic Statistics,2002,20(4).
[12]Jeffrey,C.F.,Giovanny,P.O.Estimating Forward-Looking Euler E-quations with GMM Estimators:An Optimal Instruments Approach[C].Working Paper,Federal Reserve Bank of Boston,2004.
[13]John H.Cochrane.Asset Pricing[M].Princeton:Princeton University Press,2001.
[14]Koenker,R.,Machado,J.A.F.GMM Inference when the Number of Moment Conditions Is Large[J].Journal Of Econometrics,1999,93.
[15]Imbens,G.W.GeneralizedMethod ofMomentsandEmpirical Likelihood[J].Journal of Business and Economic Statistics,2002,20.
[16]Imbens,G.W.,Spady,R.H.,Johnson,P.Information-Theoretic Approaches to Inference in Moment Condition Models[J].Econometric,1998,66.
[17]Brown,B.W.,Newey,W.K.GMM.Efficient Bootstrapping,and Improved Inference[J].Journal of Business and Economic Statistics,2002,20.
[18]Hall,A.R.Generalized Method of Moments[M].New York:Oxford University Press,2005.
[19]Singleton,K.J.Empirical Dynamic Asset Pricing[M].Princeton:Princeton University Press,2006.
[20]Hansen,L.P.Generalized Method of Moments Estimation[C].Working Paper,Department of Economics,University of Chicago,2007.
[21]Newey,W.K.,West,K.D.A Simple,Positive Semi-Definite,Heteroskedasticity and Autocorrelation Consistent Covariance Matrix[J].Econometrica,1987,55.

