不等間隔動態數據的灰色建模
程毛林
(蘇州科技學院 數理學院,江蘇 蘇州 215009)
0 引言
在很多實際問題中,有時采集的歷史數據不多,因而多數統計預測方法的效果往往不理想,而灰色預測方法特別適合于貧信息場合,在原始時間序列點數較少的情況下仍能作出很好的預測,尤其適合于原始數據近似符合指數規律變化且變化速度不是很快的場合,但通常建立的灰色模型如常用的GM(1,1)模型處理的是等間隔時間序列,在其它時間序列預測模型中如移動平均法、指數平滑法等也要求數據為等間隔時間序列。然而,在某些問題的考察中,原始數據為非等間隔時間序列,本文就此問題作些探討,對非等間隔時間序列分別為單調型和起伏型建立灰色模型。
1 不等間隔動態數據的灰色建模方法
1.1 單調型序列灰色建模
事物的發展大體上分為單調型和起伏型兩大類,單調型是指事物隨著時間呈遞增態勢,設單調型序列為不等間隔動態數據,記為其中為第ti年的數值,這里首先假定X(0)為非負遞增型時間序列。
對X(0)進行一次累計計算,得生成序列:
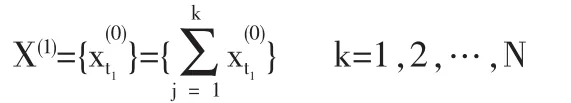

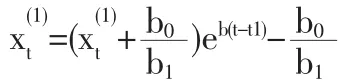
這是連續型微分方程模型,下面關鍵是估計出b0,b1為此需要進行離散化。這里設X(0)作一次累計。(1)式為

由差分和微分的關系
Δt+εt得
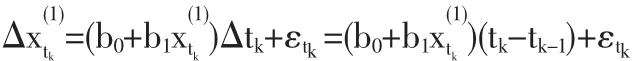
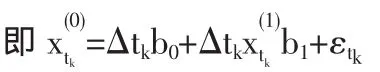

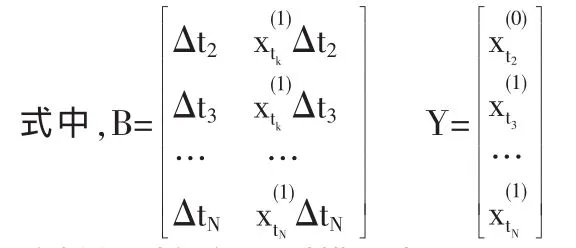
這樣得到灰色預測模型為
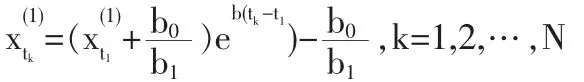
若序列是遞增的,但其值是負的或開頭的某些值是負的,則只要將數據作轉換就得到一個非負的遞增序列。若序列是遞減的,則只要作轉換就可得到遞增序列,上式M為常數,按數據量級取某一值。
1.2 起伏型序列的灰色建模
若原始序列為不等間隔起伏型動態數據,在呈近似指數規律變化同時,還呈現周期性的波動。記原始序列為為第 ti年的數值。
對X(0)進行一次累計計算,得生成序列:
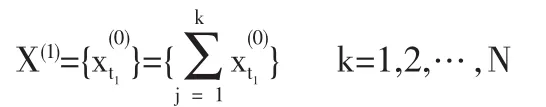
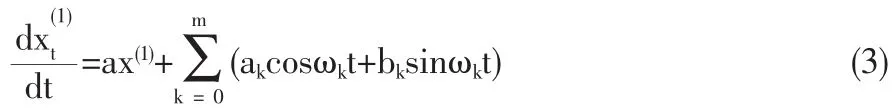
規定ω0=0,為求(3)式的解,我們先給出一般變系數線性微分方程設數據累加后X(1)滿足微分方程的解.

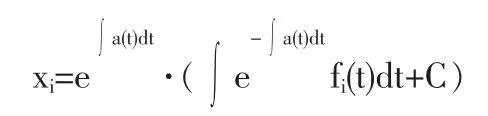
滿足初值問題的特解為
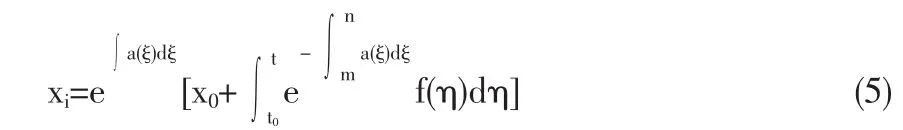
對(3)式,fi(t)=aicos(ωit)+bisin(ωit)
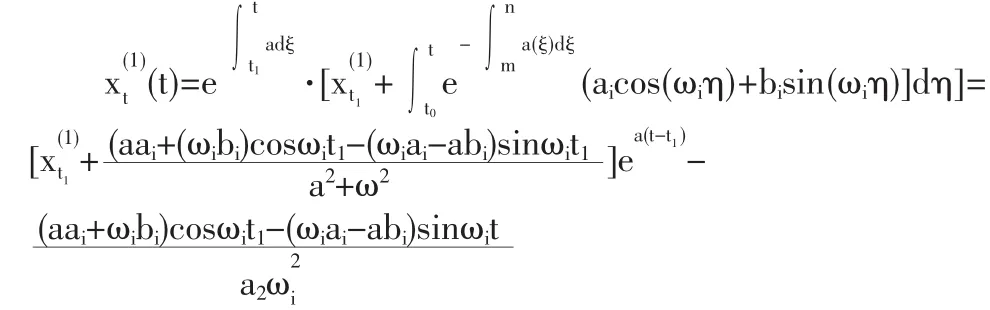

這樣(3)式的解為
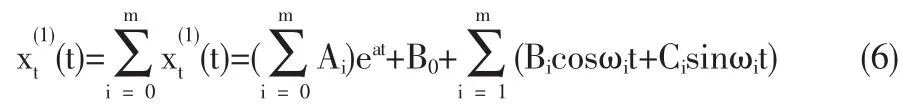
于是由
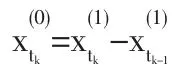
得到原始序列預測值。
現在需要對式(3)中未知變量 a、a0、a1、b1、a2、b2…am、bm、ω進行參數估計。這里給出線性化估計方法。先給出ωk的取值,N'為的 1≤N'≤N 某數值,可以通過多取幾個值,建立模型后比較誤差選取N'。
(3)式改寫成
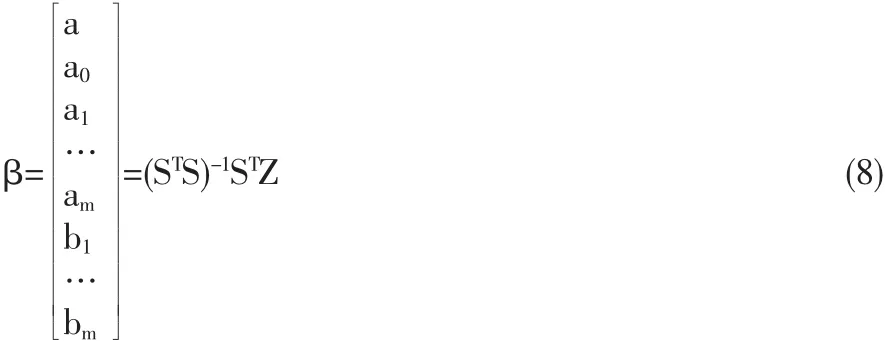
式中

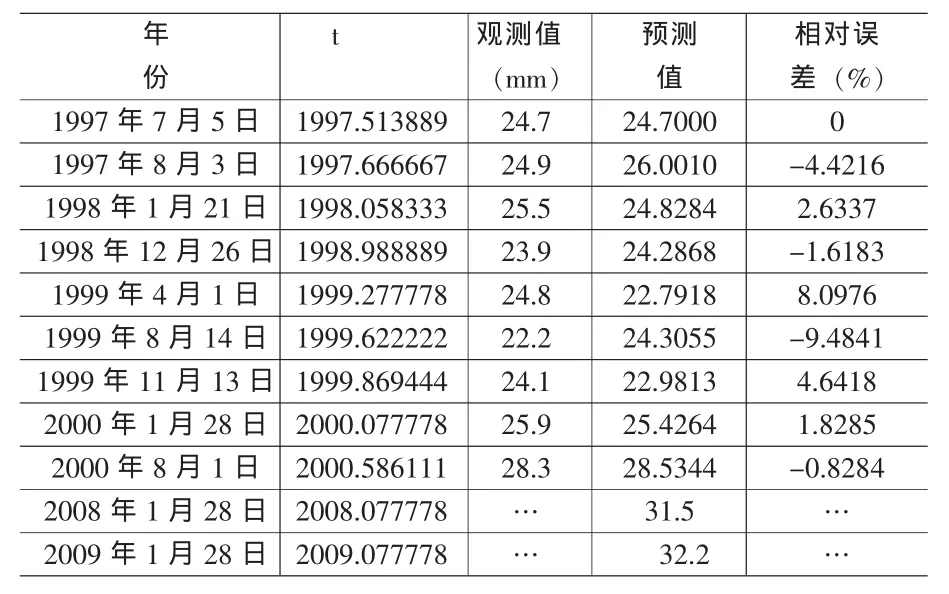
表1 蘇州虎丘塔傾斜觀測值及預測結果
這樣求出 a、a0、a1、b1、a2、b2…am、bm
于是得到(6)式,再由得原始序列的估計值。
2 不等間隔動態數據的灰色建模應用于蘇州虎丘塔傾斜預測
虎丘塔現有形變監測系統近年來建立,近年來對虎丘塔的監測一直在進行,積累了大量的觀測數據。本文采用塔基加固以后的數據進行處理和分析,討論虎丘塔維修以后至今塔體傾斜的發展趨勢。由于第八層(最頂層)的形變量代表了虎丘塔的最大形變,是判斷虎丘塔傾斜量的主要指標(見表1),這里就第八層的形變量進行預測,由于觀測的數據是不等間隔時間序列,所以采用本文方法。
從表1中的數據可以看出時間序列在緩慢上升的同時,還存在季節性的變化(溫度、雨量等季節性干擾)。
這里取 ωk=2πk/7(k=1,2,3,4)
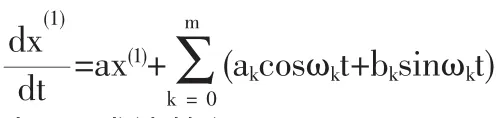
由(8)式計算得
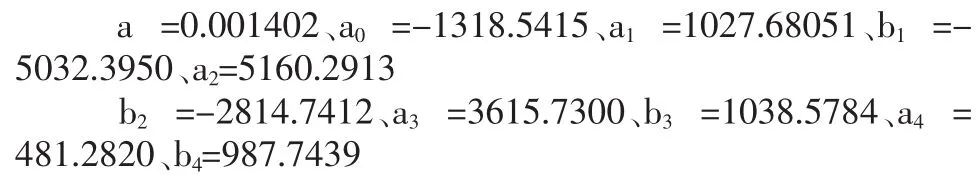
于是

[1]魏風英等.長期預測的數學模型及其應用[M].北京:氣象出版社,1990.
[2]沈繼紅等.數學建模[M].哈爾濱:哈爾濱工程大學出版社,1996.
[3]鄧聚龍.灰色控制系統[M].武漢:華中工學院出版社,1985.
[4]周紀薌.實用回歸分析[M].上海:上海科學技術出版社,1990.
[5]劉則毅.科學計算技術與Matlab[M].北京:科學出版社,2001.
[6]程毛林.不等間隔動態數據的差分建模[J].數學認識,2003,(1).

