沸石分子篩吸附和擴散：研究現狀、存在問題和展望

朱偉東， 鐘依均， 張富民，肖 強， 許春慧， 郝仕油， 代 偉

(浙江師范大學 物理化學研究所，先進催化材料省部共建教育部重點實驗室,浙江 金華 321004)

1 研究背景

沸石分子篩是一類具有骨架結構的微孔晶體材料，由于其特有的規則孔道結構(擇形選擇性，shape-selectivity)、強酸性和高水熱穩定性，在催化、分離等化學工業和石油化工領域具有廣泛的應用.因為天然沸石分子篩不能滿足工業生產的大規模需求，沸石分子篩的人工合成一直以來都受到廣泛的關注，科學家不斷地合成出具有新型結構、優異催化或吸附性能的沸石分子篩[1].另外，沸石分子篩催化的研究范圍也不斷地被擴大，在烴類轉化、選擇氧化、環境催化等多方面都有涉及[2-3].近年來，隨著科學儀器的發展改進，人們對沸石分子篩的吸附和擴散研究不斷地深入.同時，隨著計算機技術的進步，相關分子模擬(molecular simulation)技術及理論方面的研究也得到了長足發展[4-5].

吸附和擴散(adsorption and diffusion)現象不僅在科學上引起人們的高度關注，而且在工業中具有廣泛的應用[6].根據吸附質分子尺寸和形狀的不同，沸石分子篩(膜)能夠選擇性地吸附特定分子，與傳統的精餾分離工藝相比，采用沸石分子篩(膜)進行分離的能耗明顯降低.沸石分子篩的吸附擴散性能對于吸附分離至關重要，吸附質在孔道里的擴散速度往往是吸附分離的控制步驟.因此，對基于吸附的分離或純化過程來說，精確的吸附平衡數據和擴散系數的獲取對優化過程設計非常重要.

沸石分子篩的多相催化反應在現代大型石油化工和各種精細化工生產中起著舉足輕重的作用.沸石分子篩的催化性能往往與分散在沸石分子篩晶體孔道內部的催化活性中心密切相關.沸石分子篩催化反應的宏觀過程包括：1)反應物從流體主體擴散到沸石分子篩晶體的外表面(外擴散)；2)反應物從沸石分子篩晶體外表面向孔道內部擴散(內擴散)；3)在沸石分子篩晶體內部孔道的內表面上進行催化反應(化學反應)；4)產物從沸石分子篩晶體內孔道擴散到外表面(內擴散)；5)產物從沸石分子篩晶體外表面擴散到流體主體(外擴散).從優化過程設計、工業控制及開發或改良沸石分子篩催化劑等方面考慮，本征催化動力學的獲取顯得非常重要.沸石分子篩的擇形選擇性是用以描述只有大小、形狀與沸石分子篩孔道相匹配的分子才能進入沸石分子篩孔道并被吸附或催化的現象.由于分子大小要與沸石分子篩孔道尺寸相當，從而使得分子在沸石分子篩孔道里的擴散速度較慢，限制了分子在沸石分子篩中的傳質速率(即擴散限制)，由此嚴重影響了沸石分子篩催化劑的活性、選擇性等性能[7].因此，探討吸附物種在納米尺寸范圍的擴散效應對沸石分子篩催化反應動力學的影響具有重要的學術價值.同時，這些研究將為沸石分子篩催化劑的設計、制備及使用條件提供重要的指導作用，可加深對催化過程中發生的復雜反應動力學行為的認識.

2 研究現狀

2.1 吸附

表征單組分體系在沸石分子篩晶體中吸附的常規實驗技術是體積法和重量法，在過去的數十年里，在系統靈敏度、操作范圍和自動化程度等方面，這兩種常規實驗技術都得到了極大的提高[8].目前，應用這兩種常規實驗技術，可以精確地測定單組分物種在沸石分子篩晶體中的平衡吸附量.此外，隨著計算機科學的不斷發展，應用蒙特卡羅(Monte Carlo)法可以模擬和預測單組分物種在沸石分子篩晶體中的平衡吸附量，并能與實驗測定值很好地吻合.最近，Smit和Maesen[5]在國際權威刊物《化學評論(Chemical Reviews)》上對分子模擬技術在研究沸石分子篩吸附、擴散及擇形選擇性等方面的應用作了全面回顧及評述.鑒于已報道的大量實驗結果與分子模擬預測結果相一致，他們指出目前分子模擬技術可以代替“實驗”用于精確地“測定”單組分物種在沸石分子篩晶體中的平衡吸附量.圖1[9]比較了異丁烷(isobutane)在純硅(疏水性)沸石分子篩silicalite-1上的實驗等溫線和分子模擬結果，可以看到兩者具有一致性.文獻[10]通過實驗觀察到直鏈和支鏈烷烴在silicalite-1上的吸附性質之間的差異，提出了“不同分子定位”的概念，并通過分子模擬對此予以證明[11].根據具有2個不同空間的體積填充過程，分子模擬對吸附給出了令人滿意的解釋，并且與實驗結果一致.基于這樣的事實，文獻[12-13]進一步提出了一個用于描述烷烴類分子在沸石分子篩silicalite-1上等溫吸附的雙位朗繆爾(dual-site Langmuir,DSL)模型：

(1)

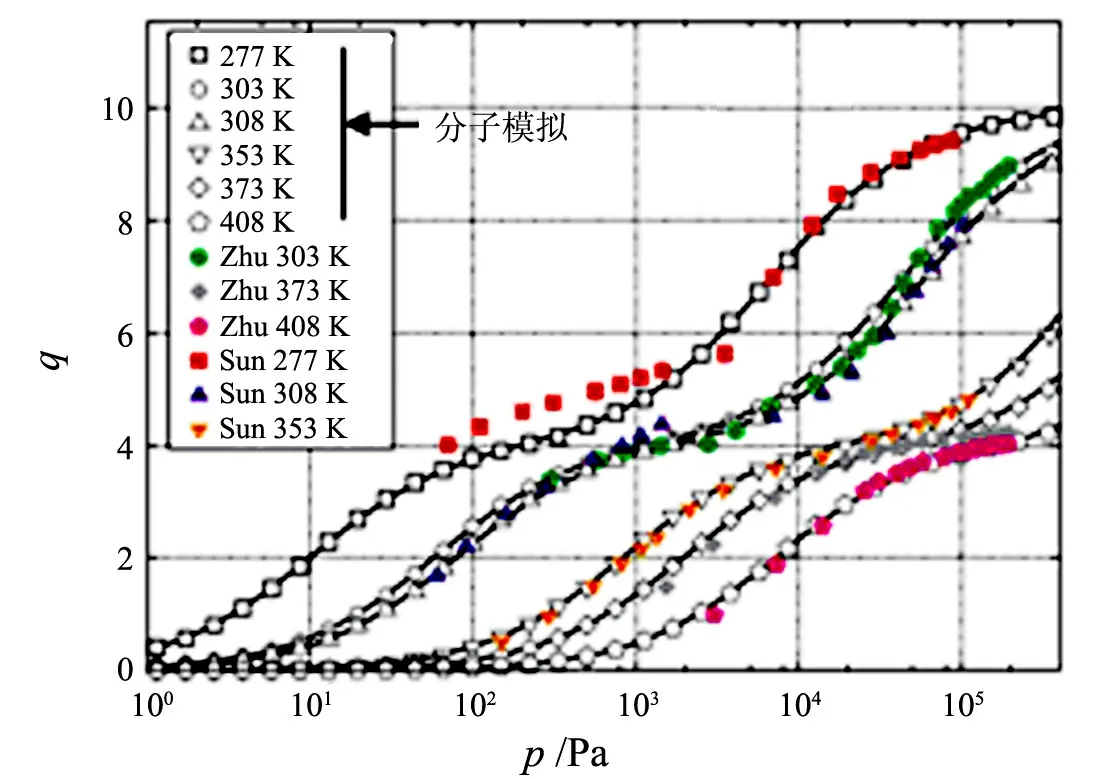
吸附量q的單位為單位晶胞分子數

如圖2所示，DSL模型很好地描述了正丁烷和異丁烷在silicalite-1上的吸附行為.總之，無論是實驗手段還是分子模擬技術，都能很好地測定和預測單組分物種在沸石分子篩晶體中的平衡吸附量[12-14].

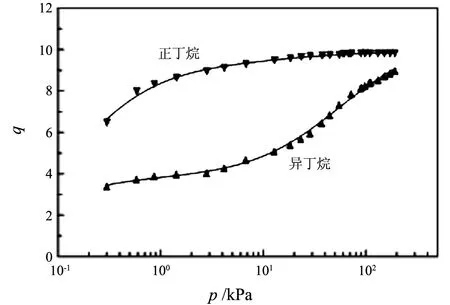
吸附量q的單位為單位晶胞分子數

沸石分子篩在催化反應和吸附分離的實際應用中，多組分體系的吸附行為常基于實驗所測得的純組分吸附等溫線，通過選擇合適的理論模型(如理想吸附溶液理論，ideal adsorbed solution theory,IAST[15])來預測混合體系的吸附行為[14].但這種預測有時會產生很大的偏差，甚至與實驗結果呈相反的趨勢.因此，應用合適的實驗手段測量多組分體系在沸石分子篩中的平衡吸附量具有重要的理論研究意義和應用價值.然而，迄今為止，關于多組分體系在沸石分子篩中的平衡吸附量實驗值的報道很少.這是由于沒有一種實驗手段可以直接確定吸附相物種的濃度，只能通過間接的實驗方法測定多組分體系的平衡吸附量，導致數據處理繁復、極其耗時，且有時受分析手段的限制而無法實施[8].

然而，隨著分子模擬技術和理論的不斷發展，模擬和預測多組分體系在沸石分子篩晶體中的吸附成為可能，大量模擬結果已見報于近期《化學評論》[5].模擬結果顯示，多組分體系在沸石分子篩中的吸附行為符合理想吸附溶液理論.如圖3所示，正丁烷-異丁烷混合體系在沸石分子篩silicalite-1上的分子模擬吸附等溫線與IAST預測完全吻合；對正丁烷的吸附分離因子隨著氣相總壓力的增加而增大.與之相比，筆者利用穿透柱(breakthrough column)技術，結合Interscience Compact GC快速檢測流出相中正丁烷和異丁烷的濃度，獲得了該雙組分體系在silicalite-1上的吸附等溫線和分離因子，實驗所測對正丁烷的選擇性隨著氣相總壓力的增加而減小.由于丁烷異構體的分子形狀及大小不同，導致它們在silicalite-1晶體內的吸附定位不同：含支鏈的異丁烷分子傾向于吸附在直型孔道(straight channels)與Z字型孔道(zig-zag channels)相接的交叉孔道(intersections)里；而直鏈烷烴正丁烷傾向于吸附在直型和Z字型孔道里[12].由此，silicalite-1對丁烷異構體呈現吸附異性，然而經典的IAST無法描述該雙組分體系在silicalite-1上的吸附行為.

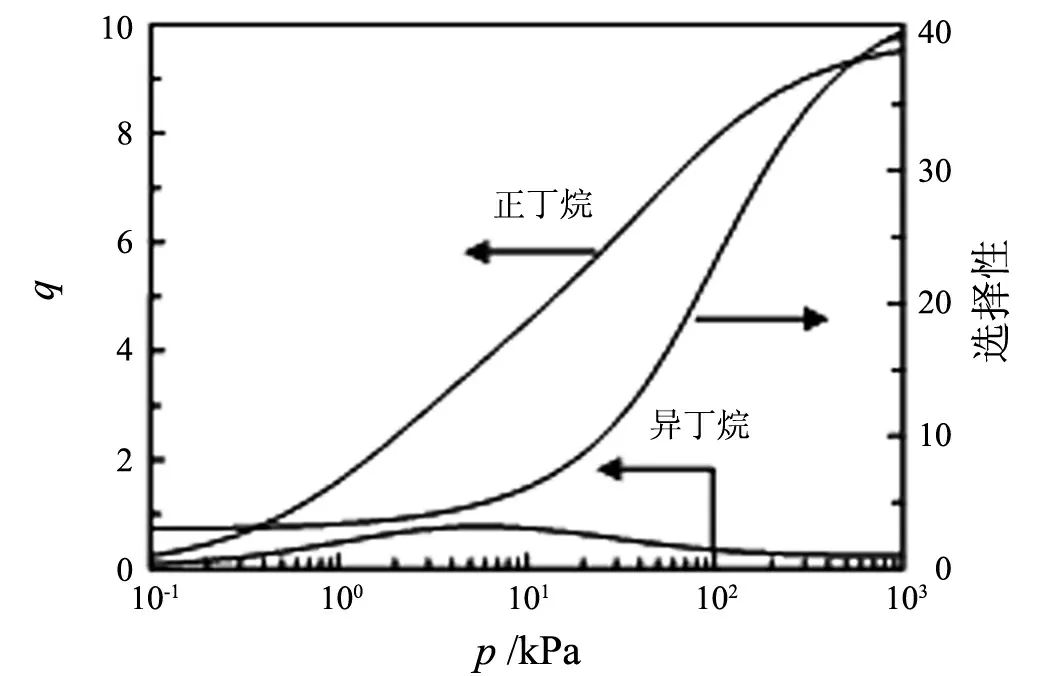
吸附量q的單位為單位晶胞分子數

2.2 擴散

研究分子在沸石分子篩中的擴散機理一直被視為一項富有挑戰性的工作.迄今，已有多種實驗技術應用于測定探針分子在沸石分子篩微孔道內的擴散系數，各種測定沸石分子篩內擴散系數(intracrystalline diffusivity)的實驗技術、實驗原理及它們的優缺點見表1.

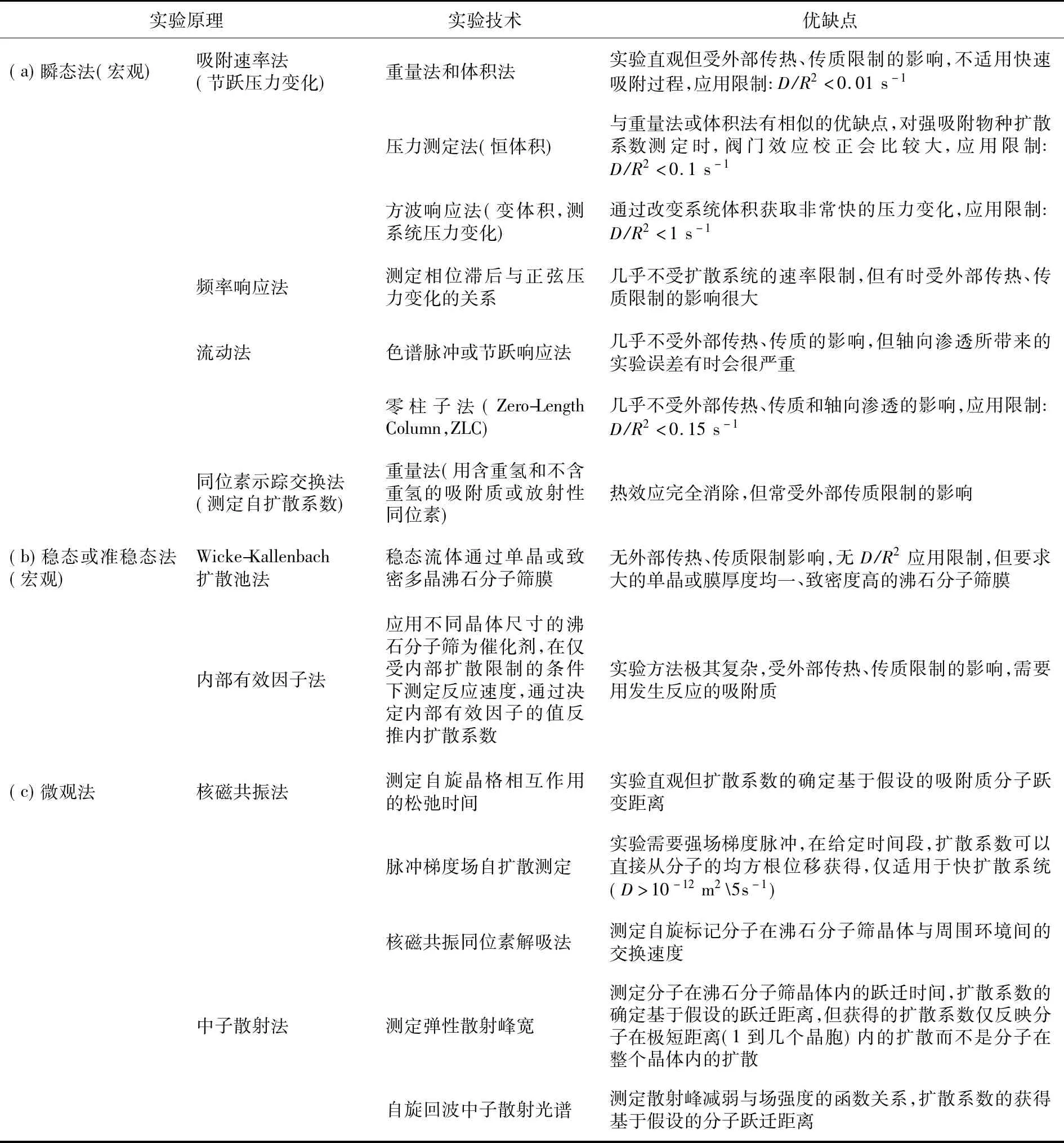
表1 測定沸石分子篩內擴散系數的實驗方法

宏觀方法確定沸石分子篩晶體內擴散系數都是建立在測定探針分子從晶體外表面進入并通過晶體的流量的基礎上，在明確的邊界條件下，運用Fick第一定律推算內擴散系數，所測得的擴散系數叫傳遞擴散系數(transport diffusivity，Dt)，或Fick擴散系數.

J=-Dt▽c.

(2)

式(2)中:J是流體流量；c指擴散物種的濃度.在宏觀方法中，實驗上給予系統一個濃度梯度，但從熱力學的角度看，擴散的驅動力(driving force)是化學勢梯度(chemical potential gradient).由此，式(2)可寫成

▽μ=-DMS▽μ.

(3)

式(3)中:L是單組分Onsager輸移系數；μ是化學勢；DMS稱校正(corrected)擴散系數或稱Maxwell-Stefan擴散系數.為了建立Maxwell-Stefan擴散系數DMS與傳遞擴散系數Dt間的關系，定義熱力學校正因子Γ為

(4)

由此，

▽μ=Γ▽c.

(5)

即通過熱力學校正因子Γ，可以建立Dt與DMS間的關系

Dt=ΓDMS.

(6)

當吸附質在沸石分子篩中的濃度很低時，Γ值接近1，這時傳遞擴散系數等于Maxwell-Stefan擴散系數，否則，熱力學校正因子需根據所測得的吸附平衡方程而獲得

(7)

式(7)中：p是平衡壓力;q是吸附量.對于Langmuir吸附方程

(8)

式(8)中,θ是吸附占有率(occupancy).顯然傳遞擴散系數Dt隨著吸附量的增加而增大.

由微觀方法所測得的擴散系數稱為自擴散系數(self-diffusivity,Ds)，通過確定分子完成一次躍遷所需平均位移時間而計算得到.迄今，所有微觀方法存在一個普遍缺點，即自擴散系數的確立是建立在假設的躍遷距離基礎上.理論上，吸附相濃度較低時，自擴散系數等于Maxwell-Stefan擴散系數或校正傳遞擴散系數,即

Ds(0)=DMS.

(9)

此外，自擴散系數隨著吸附相濃度的增加而減小，這與傳遞擴散系數與吸附相濃度間的關系呈相反的趨勢：

Ds=Ds(0)(1-θ).

(10)

分別應用宏觀方法和微觀方法對同一體系進行實驗測定，所測得的擴散系數會有很大的差異，不僅所測得擴散系數與吸附相濃度的變化呈相反趨勢，而且由2種方法分別獲得的低吸附相濃度時的擴散系數有數量級上的差異[16].圖4是用不同方法測得的低吸附相濃度時丙烷在silicalite-1上的擴散系數.顯而易見，常用的宏觀技術，例如：ZLC,Wicke-Kallenbach和頻率響應(frequency response)法，獲得基本一致的實驗值；而相比較，用脈沖梯度場核磁共振(pulsed field gradient NMR,PFG-NMR)法所測擴散系數要高2個數量級.這種差異迄今還沒有一個完整的理論解釋[16].

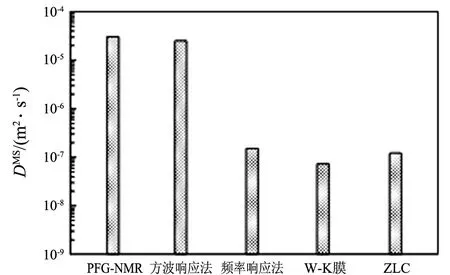
圖4 微觀和宏觀實驗技術在334 K和低吸附相濃度時測得丙烷在silicalite-1中的自擴散系數及校正傳遞擴散系數的比較[16]

近年來，分子模擬技術在預測沸石分子篩擴散系數方面得到了廣泛應用，模擬所得擴散系數及它們與吸附相濃度間的關系與微觀實驗法所測結果基本一致[4-5].微觀實驗法和分子模擬技術在“分子水平”上研究探針分子在沸石分子篩微孔道內的擴散機理，極大地豐富了該領域的理論，但它們的“實驗條件”與工業應用條件差異很大.相對而言，宏觀法(例如：ZLC和Wicke-Kallenbach技術)的實驗條件與沸石分子篩在工業應用時的條件更接近.事實上，到目前為止，在分離及催化過程設計中，所用沸石分子篩擴散系數大都來自宏觀法測定.

多組分體系在沸石分子篩中的擴散，由于其復雜性，一直被視為化工傳質領域的一大難題.迄今，國際上應用較為廣泛的理論模型是由荷蘭Amsterdam大學Krishna教授提出的廣義Maxwell-Stefan方程(generalized Maxwell-Stefan,GMS)[17-18].在單組分擴散情況下，化學勢差是驅動力；但對于混合物來說，還包括分子間作用力(“摩擦”或“交換”)

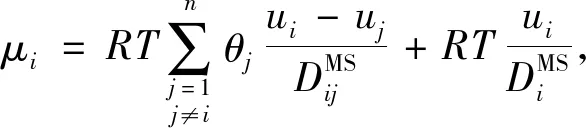
i=1,2,…,n.

(11)

如同單組分體系的情況下，化學勢差可以用所有組分的吸附量表示為

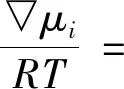
(12)

式(12)中，熱力學校正因子為

i,j=1,2,…,n.

(13)

值得注意的是，由于不同分子的大小和幾何形狀的差異，使得其在沸石分子篩上具有不同的飽和吸附量，因此，式(13)包含組分i和j的飽和吸附量.考慮這種特性，GMS公式以流量和吸附量表示[19-20],即

▽

i=1,2,…,n.

(14)

以矢量-矩陣符號表示，式(14)轉化為

(J)=-ρ[B′]-1[Γ](▽θ)=

-ρ[qsat][B]-1[Γ](▽θ).

(15)

矩陣元素：

(16)

[qsat]是飽和吸附量的一個對角矩陣.對雙組分體系，流量的明確表達式為:

(17)

(18)

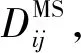
(19)

Maxwell-Stefan方程結合理想吸附溶液理論已應用于多組分體系在沸石分子篩中的傳質研究，大部分研究工作基于分子模擬[4-5]，而建立在實驗工作基礎上的研究論文報道甚少[20-22].最近，Krishna等[18]通過分子模擬指出：對于孔道型(channel type)沸石分子篩(例如MFI)應用GMS方程結合IAST時，必須考慮擴散物種間的相互作用，即Maxwell-Stefan交換擴散系數(exchange diffusivity)；相反，對于籠子型(cavity type)沸石分子篩(例如DDR)，擴散物種間的相互作用可以忽略.但這一分子模擬結果還未得到實驗證實.

3 存在的科學問題

鑒于以上討論，在沸石分子篩吸附和擴散研究領域，存在如下重要科學問題：

1)分子模擬結果顯示，silicalite-1對烷烴異構體呈現吸附異性，但經典的理想溶液吸附理論仍能很好地描述該雙組分吸附行為.用實驗方法驗證這一分子模擬結果勢在必行.

2)微觀實驗方法或分子模擬技術測得或預測的自擴散系數隨著吸附相濃度的增加而減少，這與經典擴散理論和宏觀實驗方法所觀察到的結果呈相反趨勢.而目前，宏觀實驗方法研究探針分子在沸石分子篩中的擴散的大部分工作局限于測定低吸附量時(線性處)的擴散系數，但在實際工業應用中，分子在沸石分子篩中的吸附量在非線性處.因此，實驗研究探針分子在較高吸附相濃度時的擴散機理具有十分重要的科學意義和工業應用價值.

3)Smit和Maesen[5]指出，用微觀實驗方法或分子模擬技術測定或預測分子在多維孔道沸石分子篩(如silicalite-1)中的一個特定微孔道里的擴散系數，而用宏觀方法則測定探針分子在整個晶體內的傳遞擴散系數，由此導致它們間的差異.那么能否利用宏觀實驗方法測定探針分子在一個特定的微孔道內的擴散系數？

4)應用Maxwell-Stefan方程研究多組分體系在沸石分子篩中的傳質，需要結合由混合物吸附方程而得到的熱力學校正因子Γij.如果實驗證明理想吸附溶液理論不能描述混合物的吸附行為(例如丁烷異構體在silicalite-1上的吸附)，則必須建立新的混合物吸附方程，方能更確切地闡述多組分體系在沸石分子篩中的擴散機理.

4 展 望

基于國內外在沸石分子篩吸附和擴散研究領域所共存的重要科學問題，本研究小組以烷烴異構體在silicalite-1及二氧化碳和甲烷在DDR型沸

石分子篩中的吸附和擴散為體系，將展開全面而深入的研究.選擇silicalite-1和DDR沸石分子篩為研究體系，其理由是：1)無論是實驗研究還是分子模擬，在沸石分子篩吸附和擴散研究領域，silicalite-1是迄今研究最多的一種沸石分子篩[5]，但如前述，仍有大量的科學問題有待解決；2)基礎研究已顯示，silicalite-1在烷烴、二甲苯異構體的分離上有廣闊的應用前景[20,23]，而純硅DDR型沸石分子篩能有效地分離CO2，在天然氣凈化領域有潛在的應用價值[22]；3)同屬MFI型的ZSM-5沸石分子篩在石油化工領域里是應用最廣泛的催化劑之一[2-3]；4)Silicalite-1屬孔道型而DDR屬籠子型沸石分子篩，它們代表了沸石分子篩的2種典型的結構類型.

本研究小組將合成高純度silicalite-1和DDR型沸石分子篩晶體，且晶體形貌一致、大小均勻，研究丁烷和己烷異構體在silicalite-1晶體中的混合吸附及CO2和甲烷在DDR晶體中的混合吸附；合成晶軸有序的silicalite-1膜及膜厚度均一、致密度高的DDR膜；應用ZLC和Wicke-Kallenbach(膜)技術測定單組分體系的擴散系數，重點考察吸附相濃度與擴散系數間的關系；測定兩組分混合體系通過silicalite-1和DDR沸石分子篩膜的流量，建立溫度、壓力與流量間的關系.

在此基礎上，提出新的混合物吸附理論模型，用于描述烷烴異構體混合物(例如：正丁烷與異丁烷，正己烷與3-甲基戊烷)在silicalite-1(由于烷烴異構體的分子形狀、大小不同，導致它們在silicalite-1孔道內的吸附定位不同)和CO2與甲烷混合物在DDR(吸附質分子間強相互作用)中的非理想吸附行為；基于實驗所測單組分體系擴散系數，建立沸石分子篩傳遞擴散系數與吸附相濃度間的方程；從實驗角度驗證Maxwell-Stefan方程應用于研究多組分體系在沸石分子篩中的擴散機理的可靠性，在此基礎上修正或發展新的模型；闡明利用微觀和宏觀實驗方法對同一體系所測擴散系數差異的內在原因.

參考文獻：

[1]徐如人，龐文琴.分子篩與多孔材料化學[M].北京:科學出版社，2004.

[2]Corma A.From microporous to mesoporous molecular sieve materials and their use in catalysis[J].Chem Rev,1997,97(6)：2373-2419.

[3]Corma A,Carcia H.Lewis acids:From conventional homogeneous to green homogeneous and heterogeneous catalysis[J].Chem Rev,2003,103(11)：4307-4365.

[4]Keil F J,Krishna R,Coppens M O.Modeling of diffusion in zeolites[J].Rev Chem Eng,2000,16(2)：71-197.

[5]Smit B,Maesen T L M.Molecular simulations of zeolites:Adsorption,diffusion,and shape selectivity[J].Chem Rev,2008,108(10)：4125-4184.

[6]Do D D.Adsorption analysis:equilibrium and kinetics[M].London:Imperial College Press,1998.

[7]Corma A,Fornes V,Pergher S B,et al.Delaminated zeolite precursors as selective acidic catalysts[J].Nature,1998,396：353-356.

[8]Talu O.Needs,status,techniques and problems with binary gas adsorption experiments[J].Adv Colloid Interface Sci,1998,77：227-269.

[9]Dubbeldam D,Calero S,Vlugt T J H,et al.Force field parametrization through fitting on inflection points in isotherms[J].Phys Rev Lett,2004,93(8):0883021-0883024.

[10]Zhu W,van de Graaf J M,van den Broeke L J P,et al.TEOM:A unique technique for measuring adsorption properties.Light alkanes in silicalite-1[J].Ind Eng Chem Res,1998,37(5)：1934-1942.

[11]Vlugt T J H,Zhu W,Kapteijn F,et al.Adsorption of linear and branched alkanes in the zeolite silicalite-1[J].J Am Chem Soc,1998,120(22)：5599-5600.

[12]Zhu W,Kapteijn F,Moulijn J A.Adsorption of light alkanes on silicalite-1:Reconciliation of experimental data and molecular simulations[J].Phys Chem Chem Phys,2000,2(9)：1989-1995.

[13]Zhu W,Kapteijn F,van der Linden B,et al.Equilibrium adsorption of linear and branched C6alkanes in silicalite-1 studied by the tapered element oscillating microbalance[J].Phys Chem Chem Phys,2001,3(9)：1755-1761.

[14]Vlugt T J H,Krishna R,Smit B.Molecular simulations of adsorption isotherms for linear and branched alkanes and their mixtures in silicalite[J].J Phys Chem B,1999,103(7)：1102-1118.

[15]Myers A L,Prausnitz J M.Thermodynamics of mixed-gas adsorption[J].AIChE J,1965,11(1)：121-127.

[16]Karger J,Ruthven D M.On the comparison between macroscopic and n.m.r. measurements of intracrystalline diffusion in zeolites[J].Zeolites,1989,9(4)：267-281.

[17]Krishna R.A unified approach to the modelling of intraparticle diffusion in adsorption processes[J].Gas Sep Purif,1993,7(2)：91-104.

[18]Krishna R,van Baten J M.Onsager coefficients for binary mixture diffusion in nanopores[J].Chem Eng Sci,2008,63(12)：3120-3140.

[19]Kapteijn F,Moulijn J A,Krishna R.The generalized Maxwell-Stefan equations for zeolites:sorbate molecules with different saturation loadings[J].Chem Eng Sci,2000,55(15)：2923-2930.

[20]Kapteijn F,Zhu W,Moulijn J A,et al.Zeolite membranes-modelling and application[M]//Cybulski A,Moulijn J A.Structured Catalysts and Reactors.2nd ed.Boca Raton:Taylor & Francis Group,2006:701-747.

[21]Zhu Weidong,Hrabanek P,Gora L,et al.Role of adsorption in the permeation of CH4and CO2through a silicalite-1 membrane[J].Ind Eng Chem Res,2006,45(2)：767-776.

[22]Van den Bergh J,Zhu W,Gascon J,et al.Separation and permeation characteristics of a DD3R zeolite membrane[J].J Membr Sci,2008,316(1/2)：35-45.

[23]Lai Zhiping,Bonilla G,Diaz I,et al.Microstructural optimization of a zeolite membrane for organic vapor separation[J].Science,2003,300(5618)：456-460.