一個(gè)新的有齊次核的Hilbert 型積分不等式及其逆

曾 崢, 謝子填

(1.韶關(guān)學(xué)院 數(shù)學(xué)與信息科學(xué)學(xué)院,廣東 韶關(guān) 512005；2.廣東肇慶學(xué)院 數(shù)學(xué)系,廣東 肇慶 526061)

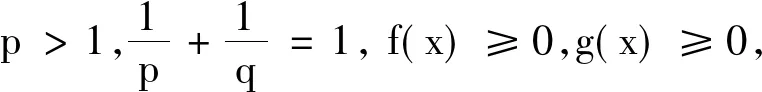
(1)

Hardy-Hilbert不等式在分析上有重要作用.近年來(lái),人們陸續(xù)對(duì)積分型和級(jí)數(shù)型的Hilbert 型積分不等式作了推廣[2-14].2008 年,筆者證明了如下有最佳常數(shù)因子的Hilbert 型積分不等式[2]:

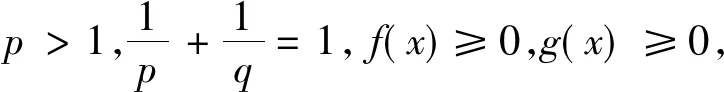
(2)

2007 年,楊必成[4]給出以下結(jié)論:

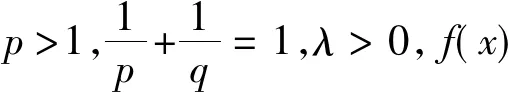
(3)

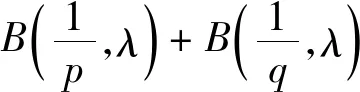
同時(shí),楊必成[5]給出以下結(jié)論:

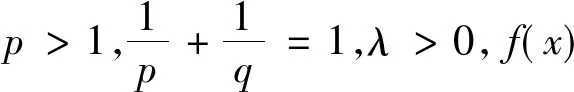
(4)

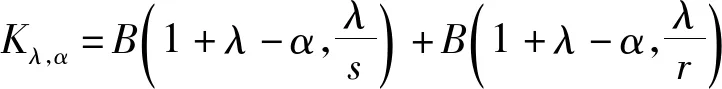
筆者將應(yīng)用權(quán)函數(shù)給出一個(gè)新的含有齊次核的Hilbert型積分不等式及其逆式，并證明了常數(shù)因子的最佳性.

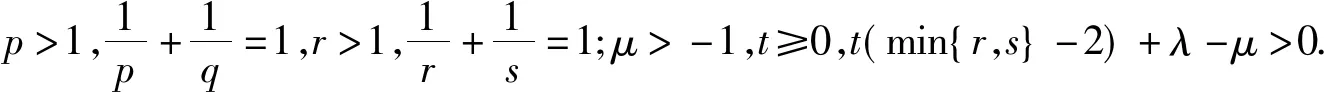
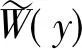
則

(5)

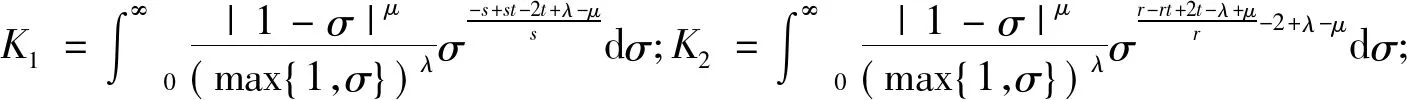
(6)

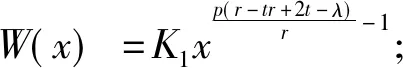
易得

引理1證畢.

(7)

(8)

且式(7)和式(8)等價(jià),常數(shù)因子K由引理1定義,K及Kp為最佳值.

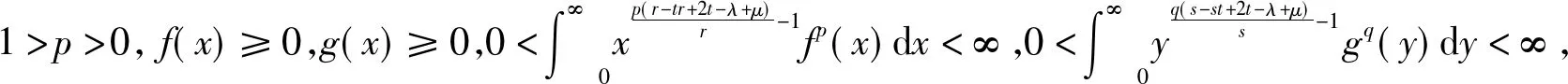
(9)

(10)

且式(9)和式(10)等價(jià),常數(shù)因子K及Kp為最佳值.

本文僅證明定理2,定理1的證明與之類似,故略.

定理2的證明 由帶權(quán)H?lder不等式[15]得

(11)

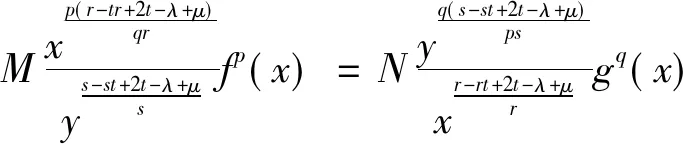
(12)

由于

(13)

故

(14)

由Fatou引理得

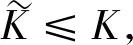
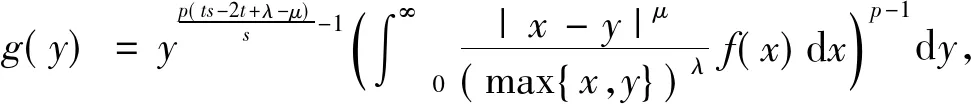
(15)

于是

(16)

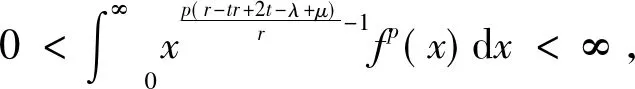
(17)

由式(16) 和式(10)即得式(9)成立,它們?nèi)?yán)格不等號(hào).綜上，式(9)和式(10)等價(jià).

參考文獻(xiàn)：

[1]Hardy G H.Note on a theorem of Hilbert concerning series of positive terems[J].Proc London Math Soc,1925,23(2):Recrds of Proc.XIV-XIVI.

[2]Xie Zitian,Zeng Zheng.A Hilbert-type integral inequality whose kernel is a homogeneous form of degree-3[J].J Math Appl,2008,339(1):324-331.

[3]鐘五一，楊必成.Hilbert 積分不等式含多參數(shù)的最佳推廣[J].暨南大學(xué)學(xué)報(bào):自然科學(xué)版,2007,28(1):20-23.

[4]楊必成.一個(gè)新的Hilbert 型積分不等式[J].吉林大學(xué)學(xué)報(bào):理學(xué)版,2007,45(1):63-67.

[5]Yang Bicheng.On a new extension of a Hilbert-type integral inequality[J].International Journal of Mathematical inequalities and Applications,2007,1(1):33-40.

[6]楊必成.一個(gè)具有混合核的Hilbert 型積分不等式及推廣[J].四川師范大學(xué)學(xué)報(bào):自然科學(xué)版,2008,31(3):281-284.

[7]謝子填,付本路.一個(gè)新的有最佳常數(shù)的Hilbert 型積分不等式[J].武漢大學(xué)學(xué)報(bào):理學(xué)版,2009,55(6):637-640.

[8]謝子填,曾崢.一個(gè)含有參量的Hilbert 型不等式[J].湘潭大學(xué)自然科學(xué)學(xué)報(bào),2007,29(3):24-28.

[9]謝子填,梁剛.一個(gè)Hilbert 型不等式及其逆[J].肇慶學(xué)院學(xué)報(bào)，2007，28(2)：14-17.

[10]謝子填,周方敏.有最佳常數(shù)的Hilbert 型不等式的推廣[J].四川師范大學(xué)學(xué)報(bào):自然科學(xué)版,2009,32(5):626-629.

[11]謝子填.一個(gè)有2對(duì)共軛指數(shù)的Hilbert 型積分不等式[J].肇慶學(xué)院學(xué)報(bào)，2009，30(5)：25-28.

[12]Xie Zitian,Yang Bicheng.A new Hilbert-type inequality with some parameters and its reverse[J].Kyungpook Mathematical Journal,2008，48(1)：93-100.

[13]謝子填,慕容居敏.參量化的逆向Hilbert 型不等式[J].吉林大學(xué)學(xué)報(bào):理學(xué)版,2008，46(4):665-669.

[14]謝子填.一個(gè)核含無(wú)理式的Hilbert 型不等式[J].數(shù)學(xué)的實(shí)踐與認(rèn)識(shí),2008,38(16):128-133.

[15]匡繼昌.常用不等式[M].3版.濟(jì)南:山東科學(xué)技術(shù)出版社,2004.