多發送端拓撲結構中網絡鏈路延遲推斷方法

許鑫，何涇沙，石恒華

(1. 北京工業大學 計算機學院，北京，100124；2. 北京工業大學 軟件學院，北京，100124)

網絡透視(Network tomography)[1]作為新興的網絡測量方法已受到很多研究機構[2-7]的關注。其基本思想是利用統計學方法，分析端到端的網絡路徑級屬性信息并推斷網絡鏈路級屬性信息，以更好地檢測網絡行為及診斷網絡的性能變化。Chen等[8]認為這種方法將成為復雜網絡性能診斷和評估中最受關注的方法之一。在對基于網絡透視的鏈路延遲分布推斷研究中，Lo等[9]提出使用端到端多播測量法建立基于邏輯多播樹的離散延遲推斷模型。Shih等[10]提出使用端到端單播測量法建立有限的混合模型，采用最大似然估計(Maximum likelihood estimation, MLE)和期望最大化(Expectation maximization, EM)算法來推斷網絡鏈路延遲情況。Xia等[11]對固定和隨機這2種網絡鏈路延遲情況分別進行了研究，并對隨機情況采用混合指數模型進行建模。雖然這些方法可以較精確地推斷出網絡鏈路延遲情況，但是，這些都是針對單一發送端的情況進行研究的，對于復雜拓撲結構的網絡鏈路性能研究還較少。Bu等[12]提出采用最小方差權值平均(Minimum variance weighted average, MVWA)方法對多發送端拓撲結構的網絡鏈路丟包率和延遲分布進行研究。通過對每一個邏輯多播樹進行單獨推斷，根據所獲得的探測包數量進行加權得到融合結果。然而，這種方法沒有充分利用來自各邏輯多播樹的路徑數據，忽略了其中的關聯關系，造成最終推斷結果不精確。Rabbat等[13]通過研究網絡拓撲結構變化，探測包到達序列及時間同步等來對復雜拓撲結構的網絡鏈路丟包率進行推斷，該方法的分析過程較復雜且實現較困難。由于多播測量能有效節省帶寬且易于統計推斷[9]，本文作者采用端到端多播測量法進行推斷研究。在盡可能充分利用路徑數據的基礎上，提出一種簡單易行的針對多發送端拓撲結構的網絡鏈路延遲推斷方法。在滿足網絡平穩性、網絡鏈路延遲的時間獨立性和空間獨立性的假設下，將復雜的多發送端拓撲結構的網絡分解成多個分解單元，并根據各分解單元所含鏈路數量的升序依次推斷各分解單元中的網絡鏈路延遲分布。

1 多發送端拓撲結構分解

在滿足網絡平穩性、網絡鏈路延遲的時間獨立性和空間獨立性的假設下，本文作者提出分解排序法，即提出將多發送端拓撲結構的網絡分解為多個單發送端拓撲結構的分解單元，并按照各分解單元所含鏈路數量的升序進行排序。

1.1 假設條件

基于如下假設[2,9-10]對網絡延遲分布進行推斷研究：

(1) 網絡平穩性。每次測量時網絡保持平穩。

(2) 時間獨立性。不同數據包在同一鏈路上的延遲統計獨立，并且同分布。

(3) 空間獨立性。同一數據包在不同鏈路上的延遲統計獨立。

網絡流量突發或長時間發生延遲會造成不同數據包之間發生關聯，此時，時間獨立性不成立；經過同一路徑的不同數據流會發生相互影響，此時，空間獨立性不成立。然而，Lo等[9,14]證明了當上述假設條件不能滿足時，對網絡性能推斷的影響程度很小。同時，這些假設又有助于分析網絡屬性和結構信息，因此，本文作者基于上面的假設條件進行推斷研究。

1.2 分解單元

選擇邏輯多播樹[9]作為研究多發送端拓撲結構中的基本分解單元。定義邏輯多播樹為T = (V, L)(其中：V為節點集；L為鏈路集)。發送端節點作為邏輯多播樹的唯一根節點。節點對(k, j)表示從節點 k到節點 j的鏈路j。這里，鏈路j對應的節點就是節點j，節點k是節點j的父節點。

分解單元如圖1所示，其中：節點0是發送端節點，節點1是分支節點，并且是節點2和節點3的父節點；節點2和節點3是互為兄弟的葉節點。發送端鏈路1與鏈路2和鏈路3分別組成路徑1和路徑2。因此，基于網絡透視的延遲分布推斷模型 Y=AX[2]，根據可測的路徑i上的延遲Yi(i=1, 2)和已知的拓撲結構A，來推斷鏈路j上的延遲Xj(j=1, 2, 3)。

圖1 分解單元Fig.1 Decomposition unit

1.3 分解排序法

設多發送端拓撲結構網絡中的發送端節點個數為M，接收端節點個數為R，節點集為V，鏈路集為L。該網絡將分解出M個分解單元，每個分解單元都包括唯一發送端鏈路和多個數據流共享鏈路。多發送端拓撲結構分解過程如圖2所示，具有4個發送端拓撲結構的網絡將會被分解為4個分解單元，其中：節點對(S1, 1)，(S2, 1)，(S3, 1)和(S4, 3)分別為發送端鏈路 S1，S2，S3和S4。由于發送端節點S1，S2和S3均向接收端節點2，4，5，7和8發送數據流，發送端節點S4向接收端節點 4，5，7和 8發送數據流，因此，鏈路j(j=2, …, 8)為數據流共享鏈路。節點1和節點3為網絡的數據流匯聚節點。

設Sm(m=1, …, M)表示發送端節點，Rm表示發送端節點Sm發送的數據包所到達的接收端節點個數，且Rm≤R，Tm表示以 Sm為發送端節點的分解單元，Vm表示分解單元Tm的節點集，Lm表示分解單元Tm的鏈路集，并且 Vm?V，Lm?L，Cm表示 Lm中鏈路個數。分解排序法描述如下：

步驟1 標記發送端節點并確定分解單元個數M。

步驟2 劃分出M個分解單元。對于每個發送端節點Sm進行如下操作：從Sm出發，尋找由Sm發送的數據包達到對應的所有 Rm個接收端節點所經過的節點集Vm和鏈路集Lm，即得到分解單元Tm= (Vm, Lm)。

步驟3 依照每個分解單元Tm所包含的鏈路個數Cm的升序方式排列各分解單元，完成分解排序過程。

由于C4＜C1=C2=C3，按照上面的分解排序法，圖2中的分解單元排序為T4T1T2T3。每個數據包都標記其發送端節點，同時，保證其接收端節點能確認該數據包的發送端地址；因此，在多發送端拓撲結構的網絡中，每個分解單元Tm都可以采集到對應Rm條路徑延遲數據。通過分析這些路徑延遲數據來計算出分解單元Tm的網絡鏈路延遲分布。除對第1個分解單元計算外，其余分解單元的計算都是基于前面計算結果依次進行的。在使用相同測量次數的延遲數據時，分解單元Tm含有鏈路個數Cm越少，計算結果越精確；因此，采用鏈路個數較少的分解單元作為最先推斷對象，使得后續計算能在較好的計算基礎上進行修正。

2 分解單元的鏈路延遲分布計算方法

采用離散延遲模型[10]對網絡中的各分解單元進行鏈路延遲分布的計算。在對分解單元中的所有鏈路進行拓撲簡化后，使用最大似然估計法[15-16]對該分解單元中的網絡鏈路延遲分布參數進行估計。

2.1 離散延遲模型

設q為離散延遲模型中的量化單元，主要用來量化所有鏈路 j上的延遲 Xj(j=1, …, J)。當延遲 Xj在內時，則該延遲被量化為dq。其中：量化索引d=0, …, D；D為1個正整數。當d=0時，量化區間為 ( 0 , 0.5q]。

2.2 分解單元的計算方法

2.2.1 拓撲簡化

圖2 多發送端拓撲結構分解Fig.2 Decomposition of multiple-source topology

為便于對分解單元中的各條鏈路延遲分布進行參數估計，提出1種拓撲簡化法來分析和處理各鏈路在所屬分解單元中的拓撲結構。即對于某條鏈路，在其所屬分解單元中尋找通過該鏈路的所有路徑，通過進行拓撲簡化使得每條鏈路只屬于該分解單元中的某一條路徑。若僅有1條路徑通過，則不需要進行拓撲簡化處理。

對于某條鏈路j的拓撲簡化描述如下。

步驟1 尋找子孫節點。尋找并標記鏈路j對應節點的所有子孫節點。

步驟 2 自底向上，逐步合并。在這些子孫節點中，從深度最大(距離鏈路 j所對應節點的跳數最多)的葉節點開始，先對同父的兄弟節點進行合并，然后，與其父節點合并。依此類推，直至下一個將合并的節點為鏈路j對應的節點為止，此時得到1條路徑。

以圖2分解單元T1中的鏈路3為例，拓撲簡化過程如圖 3所示。在步驟 1中尋找鏈路 3的子孫節點，鏈路3對應節點3，節點3的所有子孫節點為節點4、5，6，7和8。在步驟2中，先合并兄弟葉節點7和8為節點(7, 8)，然后，與其父節點6合并為節點(6, (7, 8))，再與節點6的兄弟節點4，5合并為節點(4, 5, (6, (7, 8)))，此時，它們的父節點為節點3，是所求鏈路3的對應節點。可見，中止拓撲簡化，得到路徑S1-1-3-(4, 5, (6, (7, 8)))。

圖3中節點(4, 5, (6, (7, 8)))對應鏈路的延遲概率可以表達為：

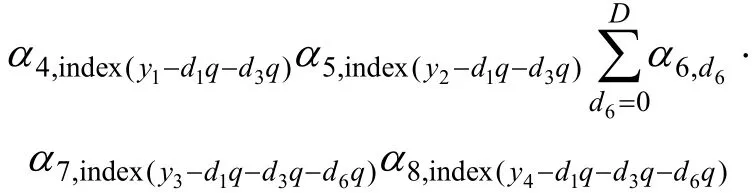
其中：dj為鏈路j上延遲的量化索引；y1，y2，y3和y4分別為到葉節點 4，5，7和 8的路徑延遲值，函數index(x)表示延遲值為x時所對應的量化索引。

2.2.2 參數估計

采用最大似然估計法[15-16]對該分解單元中的網絡鏈路延遲分布進行參數估計。

令Y為可測的端到端路徑延遲數據。第j條鏈路上延遲Xj的概率為：

因此，在給定完整延遲數據X1, …, XT的情況下，X的對數似然函數表示為：

通過EM算法求解網絡鏈路延遲分布的最大似然估計值。

令 )(k

α 表示第k次估計，最大化第k+1次目標方程為：

計算出第 k+1次估計值 α(k+1)，循環計算，直至得到滿足一定精度的網絡鏈路延遲分布的估計值為止。

3 多發送端拓撲結構中網絡鏈路延遲推斷方法

對于整體的多發送端拓撲結構，提出的推斷過程描述如下。

步驟 1 按照分解排序法分解多發送端拓撲結構的網絡，得到分解單元的排序；

步驟2 依次選擇分解單元Tm，按照分解單元計算方法對Tm中所有鏈路進行拓撲簡化，使用其對應的Rm條路徑延遲數據進行最大似然估計，計算發送端鏈路和數據流共享鏈路的延遲分布，此時，將數據流共享鏈路的延遲分布作為計算下一個分解單元延遲分布的初始值，即下一次計算過程是修正前面的計算結果。

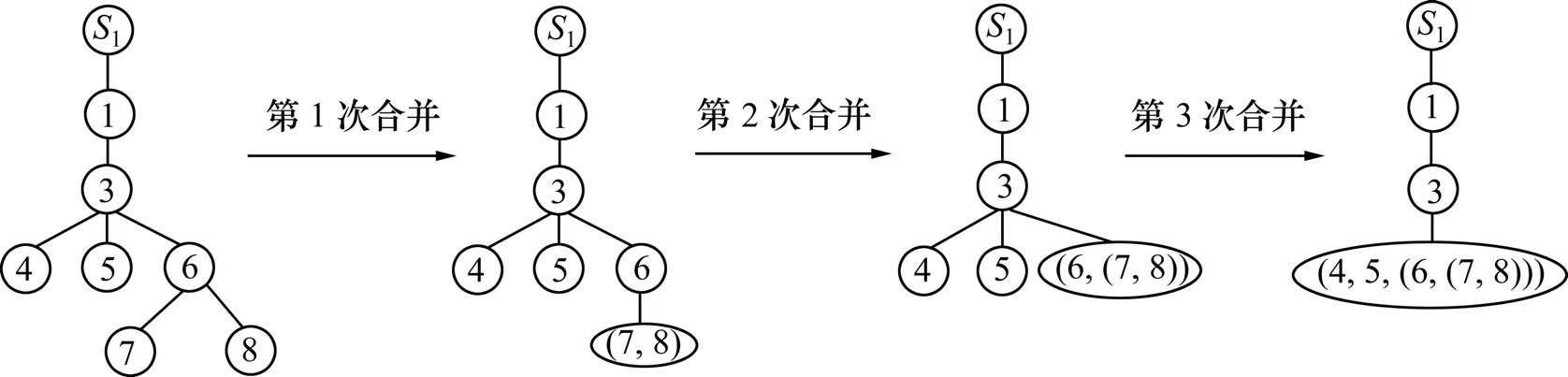
圖3 拓撲簡化Fig.3 Topology simplification

步驟3 重復步驟2，直到完成對所有分解單元的計算為止，從而得到多發送端拓撲結構中所有鏈路的延遲分布情況。

其中，發送端鏈路只包含于1個分解單元中，因此，只使用所在分解單元的路徑延遲數據進行1次計算，而數據流共享鏈路可以使用包含它的所有分解單元的路徑延遲數據進行多次計算。

4 仿真實驗

4.1 實驗平臺

使用 OPNET仿真軟件進行多發送端拓撲結構的網絡延遲實驗。網絡拓撲如圖4所示。節點對(S1, 1)，(S2, 1)，(S3, 1)和(S4, 3)分別為發送端鏈路 S1，S2，S3和S4，其余鏈路均為數據流共享鏈路。

4.2 實驗設置

圖4中各鏈路的數據傳送速率如表1所示，各發送端節點發送的數據包屬性如表2所示。實驗仿真時間為1 000 s，選擇量化單元q=0.1，共有40個量化區間。在每條鏈路上采集1 000個點作為該鏈路延遲的真實值，并采用同一量化單元q=0.1進行量化，統計得到各鏈路延遲的真實分布情況，用于與本文作者提出的方法的推斷結果進行對比。

根據分解排序法，得到分解單元的推斷順序為T4T1T2T3，即：首先計算分解單元T4得到鏈路S4及數據流共享鏈路4，5，6，7和8上的延遲分布估計值；將這些數據流共享鏈路上的延遲分布估計值作為計算分解單元T1中對應鏈路上的延遲分布初始值，以得到鏈路S1及數據流共享鏈路2，3，4，5，6，7和8上的延遲分布估計值；將這些數據流共享鏈路上的延遲分布估計值作為下一個分解單元 T2中對應鏈路上的延遲分布初始值。依此類推，計算得出所有鏈路上的延遲分布估計值。

圖4 多發送端的網絡拓撲Fig.4 Multiple-source network topology

4.3 實驗結果

4.3.1 有效性驗證

選擇非數據流共享鏈路 S1以及數據流共享鏈路2，4和8作為代表鏈路進行分析。圖5所示為這4條鏈路上的延遲分布真實值和估計值的對比結果。

如圖5(a)所示，對于非數據流共享鏈路S1，只使用分解單元T1進行網絡鏈路延遲分布估計，雖然沒有多次估計修正過程，但是網絡鏈路延遲分布估計值已經能較好模擬真實網絡的變化情況。

設Pd和Qd分別表示當量化索引為d時數據流共享鏈路 j上的延遲分布真實值和估計值，根據計算鏈路j的Pd和Qd之間的差異，其中，數據流共享鏈路4和8共進行了4次估計，結果如表3所示。

表1 各鏈路上數據傳送速率Table 1 Data rate of each link

表2 各發送端節點發送的數據包屬性Table 2 Packet properties of each source

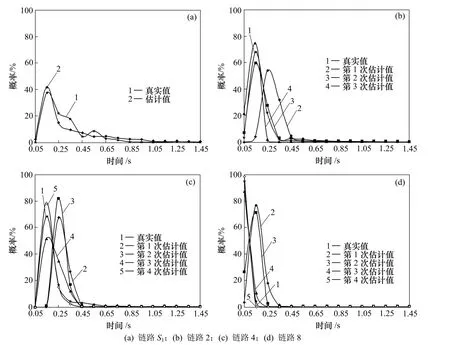
圖5 鏈路延遲分布真實值和估計值的對比Fig.5 Comparisons between true and estimated values of links delay distribution

對于數據流共享鏈路，對真實值與多次修正的估計值進行對比，結果如圖 5(b)～(d)所示。可見：每次修正結果總體上都更趨近于真實的延遲分布情況。鏈路4和鏈路8上的延遲真實值和估計值之間的差異如表3所示，可見：鏈路4和8的每次估計都使得真實值和估計值的差異減小。圖5也顯示出每次修正后的變化趨勢。

表3 鏈路4和鏈路8上的延遲真實值和估計值之間的差異Table 3 Difference between true and estimated values of delay for Link 4 and Link 8

在對多發送端拓撲結構的網絡鏈路延遲分布進行推斷研究時，要充分考慮所有分解單元中的數據流對網絡性能的影響。從圖4可見：該網絡中的4個發送端節點所產生的數據流共同影響其數據流共享鏈路，因此，只使用其中某個分解單元的路徑數據進行分析，則推斷結果只是受該分解單元中數據流影響的粗略估計值。但是，若在滿足網絡平穩性、網絡鏈路延遲時間獨立性和空間獨立性的假設條件下，使用其余分解單元的路徑延遲數據對該分解單元的粗略估計值進行多次迭代修正，則會使推斷結果更符合網絡內部的真實情況。

4.3.2 與MVWA方法的比較

采用本文作者提出的方法與 MVWA方法[12]所得的鏈路延遲分布比較結果如圖6所示。鏈路延遲分布概率越大，精度越高。從圖6可見：作者提出的方法優于MVWA方法。由于MVWA方法只是通過對每個邏輯多播樹進行單獨計算，雖然考慮了所有數據流的影響，但是，這種較簡單的通過加權得到估計值的方法卻降低了精度。而作者提出的方法在沒有增加計算復雜度的情況下，充分利用了路徑數據，通過多次估計修正達到較高的精度。

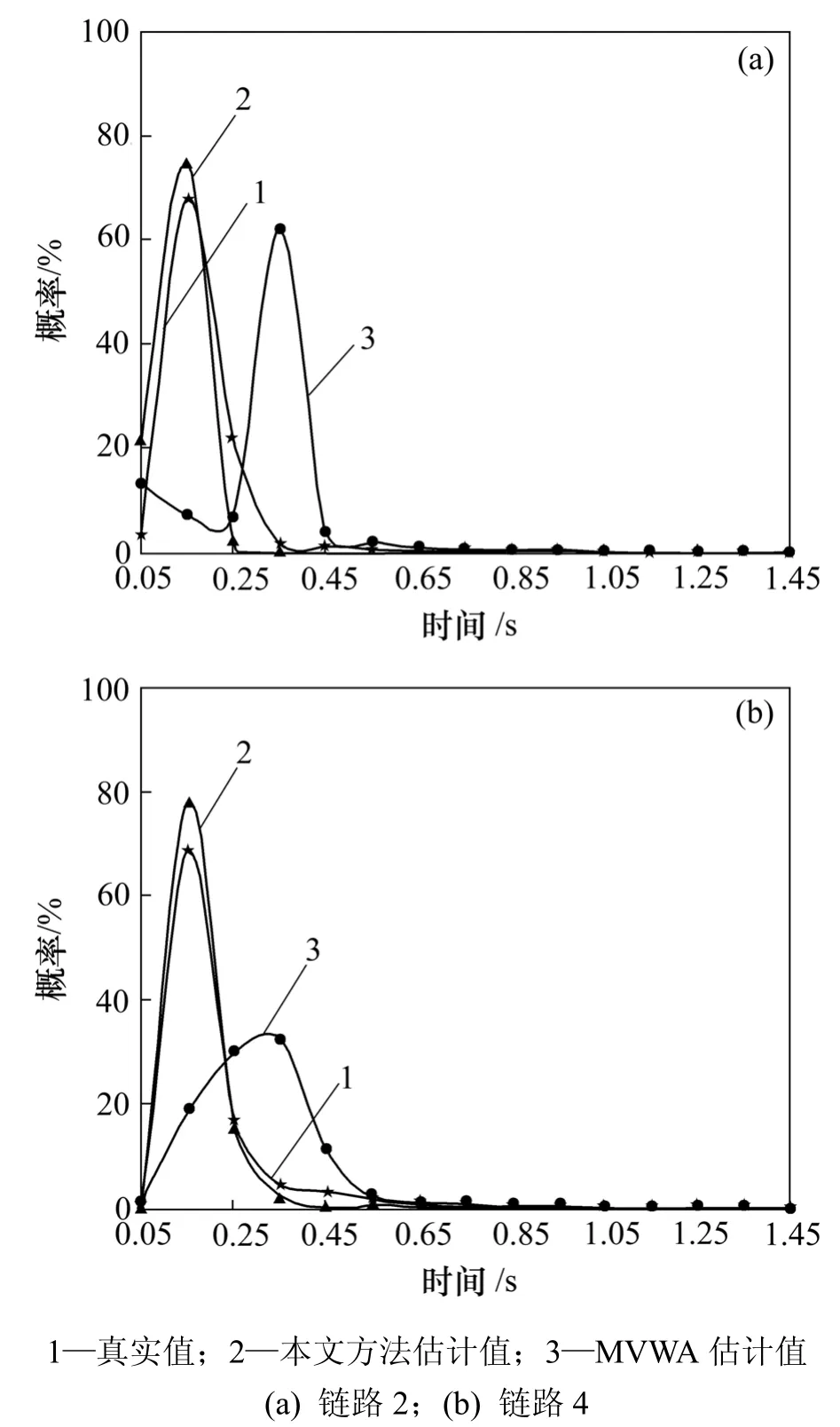
圖6 本文方法與MVWA方法鏈路延遲分布概率的比較Fig.6 Comparisons of probability of links delay distribution between method in this paper and MVWA method

5 結論

(1) 提出一種網絡鏈路延遲分布推斷方法來解決復雜的多發送端拓撲結構中網絡內部延遲推斷問題。該方法將復雜的多發送端拓撲結構的網絡分解成多個簡單的分解單元，并按照各分解單元所含鏈路個數的升序計算各分解單元網絡鏈路延遲分布。

(2) 每個分解單元的計算是在完成拓撲簡化處理后，使用最大似然估計法進行網絡鏈路延遲分布的估計。由于對每個分解單元的數據流共享鏈路延遲分布的計算，都是基于前面估計結果進行修正，因此，數據流共享鏈路延遲分布的真實值和估計值之間的差異逐漸減小，即推斷結果逐漸趨近于網絡內部的真實情況。

(3) 與MVWA方法相比，本文作者所提出的方法能更精確地推斷出多發送端拓撲結構中網絡內部鏈路延遲情況，具有較強的實用性。

[1] Vardi Y. Network tomography: estimating source-destination traffic intensities from link data[J]. American Statistical Association, 1996, 91: 365-377.

[2] Castro R, Coates M J, LIANG Gang, et al. Network tomography:recent developments[J]. Statistical Science, 2004, 52(3):499-517.

[3] Duffield N G. Network tomography of binary network performance characteristics[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5373-5388.

[4] Shih M, Hero A O. Hierarchical inference of unicast network topologies based on end-to-end measurements[J]. IEEE Transactions on Signal Processing, 2007, 55(5): 1708-1718.

[5] JIN Xing, TU Wang-qing, Gary Chan S H. Scalable and efficient end-to-end network topology inference[J]. IEEE Transaction on Parallel and Distributed System, 2008, 19(6): 837-850.

[6] Duffield N G, Lo Presti F, Paxson V, et al. Network loss tomography using striped unicast probes[J]. IEEE/ACM Transaction on Networking, 2006, 14(4): 691-710.

[7] Sharma G, Jaggi S, Dey B K. Network tomography via network coding[C]//Masimo F. IEEE Information Theory and Applications Workshop. Piscataway: IEEE, 2008: 151-157.

[8] CHEN Ai-you, CAO Jin, BU Tian. Network tomography:identifiability and Fourier domain estimation[C]//IEEE INFOCOM. Anchorage: IEEE, 2007: 1875-1883.

[9] Lo P F, Duffield N G, Horowitz J, et al. Multicast-based inference of network-internal delay distributions[J]. IEEE/ACM Transactions on Networking, 2002, 10(6): 761-775.

[10] Shih M, Hero A O. Unicast-based inference of network link delay distributions with finite mixture models[J]. IEEE Transactions on Signal Processing, 2003, 51(8): 2219-2228.

[11] Xia Y, Tse D. Inference of link delay in communication networks[J]. IEEE Journal on Selected Areas in Communications,2006, 24(12): 2235-2248.

[12] Bu T, Duffield N G, Lo Presti F, et al. Network tomography on general topologies[C]//Richard M. Proceeding of the ACM SIGMETRICS. Marina Del Rey: ACM Press, 2002: 21-30.

[13] Rabbat M G, Coates M J, Nowak R D. Multiple-source Internet tomography[J]. IEEE Journal on Selected Areas in Communications, 2006, 24(12): 2221-2234.

[14] Caceres R, Duffield N G, Horowitz J, et al. Multicast-based inference of network-internal loss characteristics[J]. IEEE Transactions on Information Theory, 1999, 45(7): 2462-2480.

[15] LIANG Gang, YU Bin. Maximum pseudo likelihood estimation in network tomography[J]. IEEE Transactions on Signal Processing, 2003, 51(8): 2043-2053.

[16] Tsang Y, Nowak R. Network tomography in theory and practice[D]. Houston: Rice University. Department of Electrical and Computer Engineering, 2005.