不同高徑比時軟巖強度與變形尺寸效應試驗研究

陳瑜，黃永恒，曹平，衣永亮，李娜，李麗娟

(中南大學 資源與安全工程學院，湖南 長沙，410083)

巖石是指由各種裂隙切割而形成的巖塊，又稱為結構體。巖石由于其生成條件及生成后數億年的地質構造作用和大氣風化作用，在巖石內部形成各種類型的空隙、微裂隙及肉眼可見的各種缺陷，它們直接影響巖石的物理力學性質，因此，不同的巖石樣本的力學性質常表現出差異，即產生所謂尺寸效應[1]。軟巖是一種在特定環境下具有顯著塑性變形的復雜巖石力學介質，其強度低，孔隙度大，膠結程度差，受構造面切割及風化影響顯著或含有大量膨脹性黏土礦物。本文所采用的實驗試件均為金川二礦區的典型軟巖。Hudson等[2]基于不同尺寸大理巖石的單軸壓縮試驗結果表明：巖石抗壓強度隨巖樣高徑比變化而變化，具有尺寸效應，但他們并沒有對巖石材料尺寸與強度的定量關系以及機理進行探討；劉寶琛等[3]對前人做過的7種巖石單軸抗壓強度試驗結果進行了分析，得到巖石強度隨試樣尺寸呈指數型衰減規律的公式；楊圣奇[4]對巖石材料的非均質性與強度尺寸效應之間的關系進行了討論，指出巖樣尺寸效應不僅體現在強度的平均值上，而且與強度的離散性相關，同時對單軸拉伸強度的尺寸效應進行了定性分析，得到巖樣單軸拉伸的平均強度隨尺度的增大而降低的規律；何滿潮等[5]通過建立工程巖體的連續性模型，研究了工程巖體力學參數的尺寸效應；周火明等[6]采用室內和現場巖體力學試驗和數值模擬等手段，對三峽永久船閘邊坡巖體宏觀力學參數進行了研究，建立了巖體變形模量與尺寸之間的關系；王學濱等[7]也利用剪切梯度塑性理論，建立了單軸受壓下巖樣尺寸效應的塑性剪切應變梯度模型。可見，巖石材料的尺寸效應現象一直是巖石力學界有待解決的問題，它直接關系到巖土工程設計、實驗和數值計算時巖石力學參數的選取和預測[8-11]。在此，本文作者在伺服機上對 2組采自金川二礦區的直徑相同而高度不同的巖石樣本進行單軸壓縮試驗，研究巖石的尺寸的高徑比與強度、變形特性和破裂形式等規律，并對相應的機理進行探討。

1 礦區地質條件

金川二礦區位于大背兒泉溝出口的洪積扇頂端下部，是1個隱伏礦床。礦區地層主要為前震旦系和第四系組成，其中：前震旦系巖層由北至南，從老到新分布，巖性主要為蛇紋石化大理巖、混合巖化片麻巖及二云片麻巖等；第四系地層廣泛分布于礦區中北部，往北與廣闊的戈壁相連。

隨著開采強度的日益加大，目前，金川礦山開采深度已超過1 km。金川二礦區礦體具有傾斜、厚大、破碎軟弱、高地應力、節理裂隙發育、巖體單塊強度高、整體強度低等地質特征。

2 試驗系統、巖性特征和試驗結果

采用的試驗系統為上海新三思微機控制電液伺服剛性試驗機。實驗采用位移控制，荷載-位移全過程曲線由x-y函數記錄儀直接繪出。選用的巖石試驗樣本的巖性分別為貧礦和白云石大理巖，其力學參數見表1。其中：D和H分別為巖樣的直徑和高度；σ0為巖樣的單軸抗壓強度；ε0為巖樣的峰值應變(這里的應變指的是整個試樣的平均應變，而不是試樣中部受端部約束較小的部位的應變)；E0為巖樣的彈性模量，即應力-應變曲線上近似直線部分的平均斜率；E50為巖樣的變形模量，即巖樣峰值強度一半處對應的應力與應變的比值。

2.1 不同尺寸時巖體試件的應力-應變關系

通過試驗，得到了不同尺寸時巖樣試件卸荷的應力-應變關系曲線，結果如圖1和圖2所示。

從圖1和2可以看出：巖石樣本所能承受的最大應力隨著試樣高度的變化而變化，高度較大，最大應力值較大；高度較小，最大應力值較小；對應于試樣高度分別為48.34，78.02和96.08 mm的試件，貧礦試件的曲線斜率分別為3.172，4.915和7.596；對于試樣高度分別為51.24，82.66和98.52 mm的試樣，白云石大理巖試件的曲線斜率分別為 2.356，3.867，5.145。可見，應力-應變關系曲線的斜率隨著試件高度減小而減小；當試件高度較大時，曲線較陡，也就是試件卸荷過程中的塑性變形量較小。

2.2 變形模量和彈性模量隨尺寸的變化

巖樣彈性模量和變形模量與高徑比的關系如圖 3所示。圖3表明：隨高徑比的增加，巖柱彈性模量和極限變形模量分別都呈增加趨勢，且相關關系密切，顯示出一定規律；當高徑比分別約為1.04，1.67，2.00時，白云石大理巖巖樣的彈性模量分別為6.17，11.07和15.12，變形模量分別為1.20，2.99，3.41；貧礦巖樣的彈性模量分別為3.13，5.18和8.09；變形模量分別為0.92，1.55和2.44。2組巖樣的曲線表明：高徑比越小，彈性模量和極限變形越小；高徑比越大，彈性模量和極限變形則相應增大。由于選用數量較少的大礦柱所能支承的頂板負荷要大于數量較多的小礦柱[2]，因此，這樣的礦柱設計原理合理。

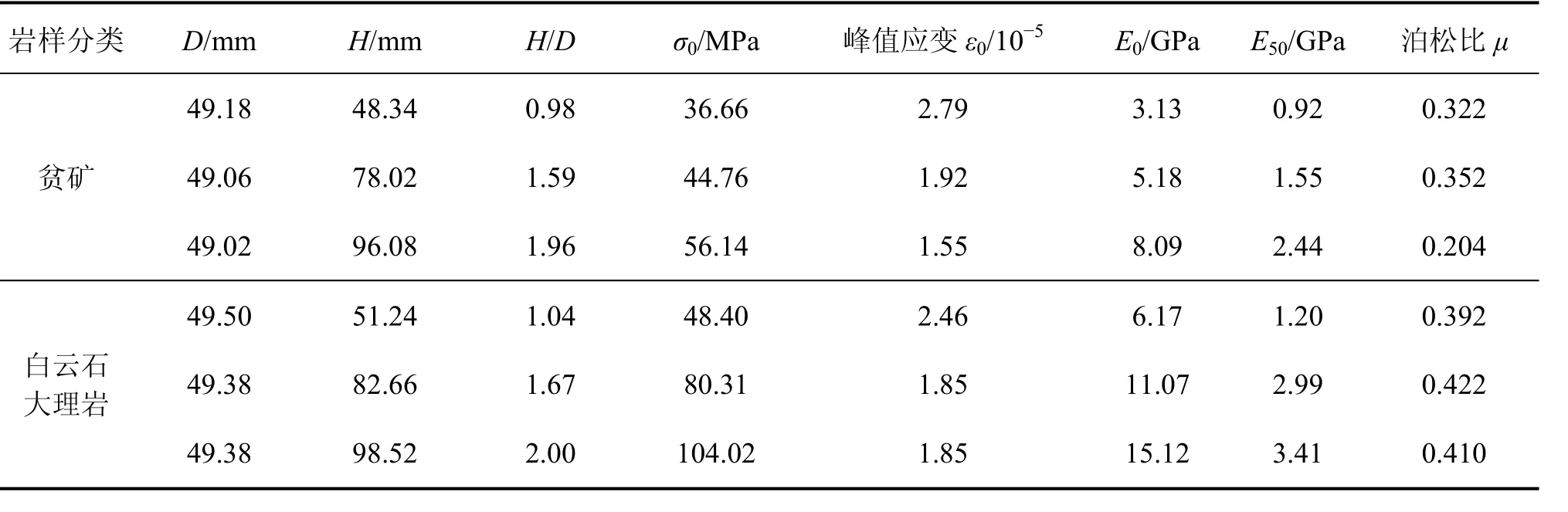
表1 巖樣的力學參數Table 1 Mechanical parameters of specimens

圖1 貧礦巖樣試件的應力-應變關系Fig.1 Relationship between strain and stress for rock sample of lean ore

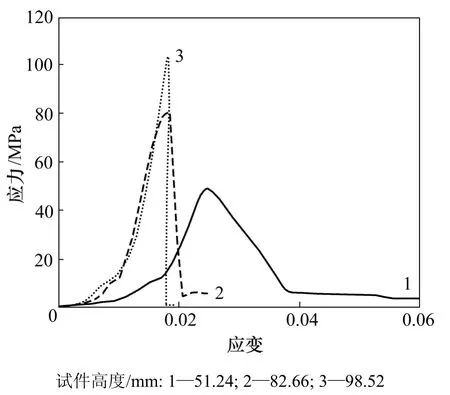
圖2 白云石大理巖巖樣試件的應力-應變關系Fig.2 Relationship between strain and stress for dolomite marble rock sample

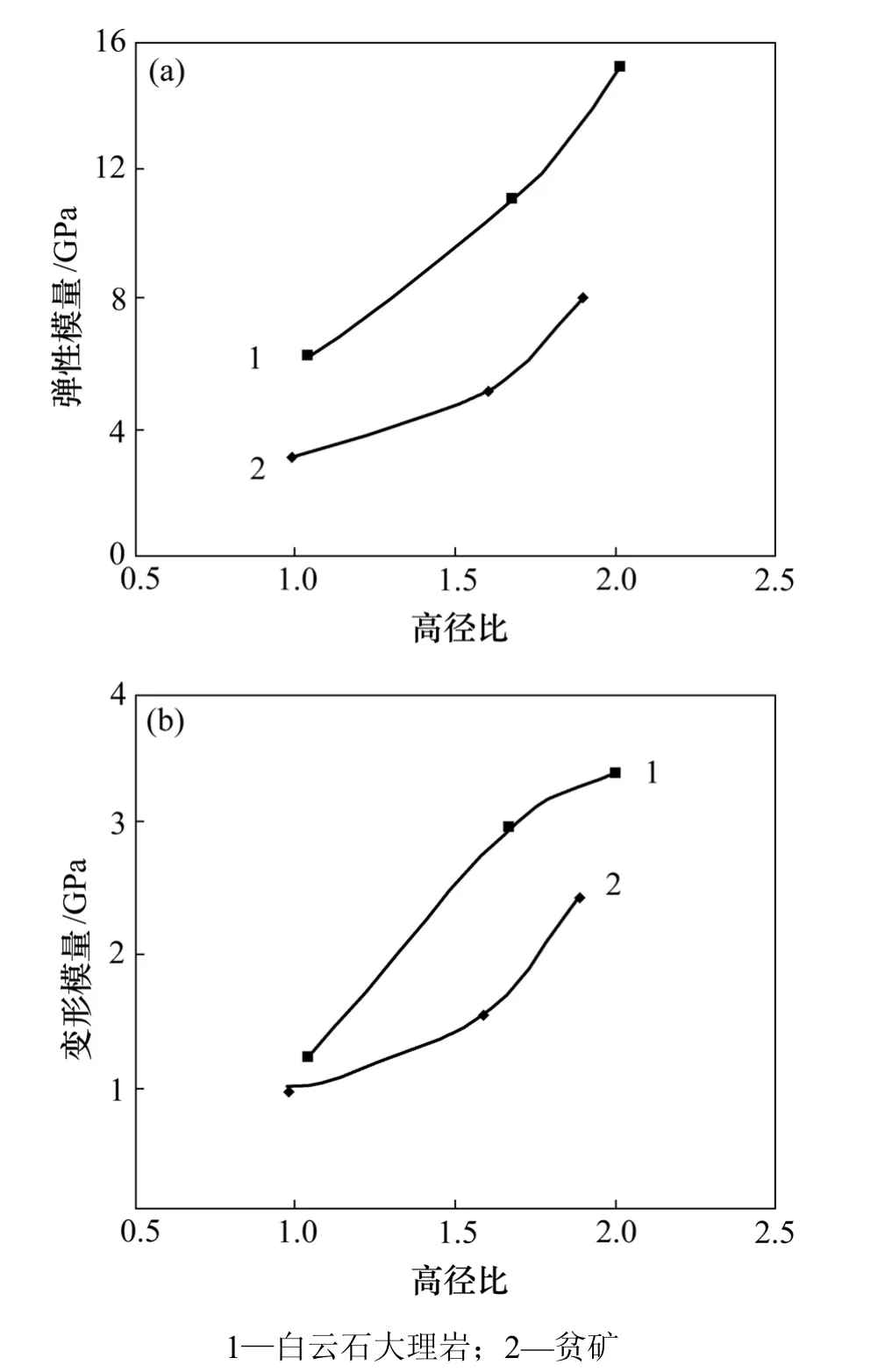
圖3 巖樣彈性模量、變形模量與高徑比的關系Fig.3 Relationship among elastic modulus,deformation modulus of rock sample and ratio of height to diameter

3 巖樣尺寸對破裂形式的影響

當巖樣直徑一定時，不同高度貧礦與白云石大理巖巖樣的破壞形式如圖4所示。

由圖4可知：當高度較小時，巖樣破壞形式較復雜，沿軸向出現較多的劈裂面，而高度較大時，巖樣基本上呈劈裂和剪切破壞。其原因是：在單軸壓縮條件下，由于上下墊板的剛度大于巖石試件的剛度，試件在壓縮下的泊松比效應因試件斷面與墊板間的摩擦而受到約束，因此，在試件兩端形成錐形壓縮區，單軸壓縮時，巖樣應該處于一維受壓狀態，從而使得巖樣上下端部附近形成了三維壓縮應力區(圖5)；高度越大的巖樣中部應力區越接近一維應力狀態，相反，高度越小的巖樣，整體均受三維應力區的影響；當直徑一定時，由于巖樣端面與鋼性墊塊之間的摩擦作用，巖樣的高度改變了其應力分布區的形式，隨著高徑比的減小，巖樣上下端部三維壓縮應力區的影響越來越大，從而使得巖樣的破壞形式變得復雜[12-13]。

圖4 2組巖樣的破壞形式Fig.4 Failure shapes of two kinds of rock specimens

當用高徑比H/D=1的圓柱形試件或高寬比為1的立方體試件時，兩端的錐形壓縮區必然互相連接，測得的抗壓強度必然大于實際值。只有墊板的剛度與巖石剛度完全相同，才能消除端部效應的影響。但對于不同的巖石，要找到剛度相同的墊板，幾乎是不可能的。國際巖石力學學會推薦用高徑比為2.5～3.0的試件做抗壓試驗，其目的就是使試件中間部分處于單軸壓縮狀態，保證測出真實的單軸抗壓強度。

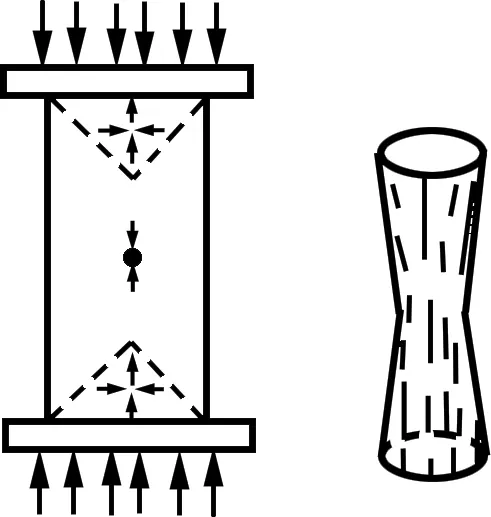
圖5 單軸壓縮時狀態中的應力分布和破壞形式Fig.5 Stress distribution and failure mode in condition of uniaxial compressive

4 抗壓強度和尺寸效應的機理

巖石強度是評價巖石工程穩定性的重要參數之一，是巖體力學研究中1個十分重要的力學指標[14-15]。研究表明：

(1) 單軸壓縮下，巖石強度隨著尺寸的增大而減小。龍明慶等[8]通過分析 7種巖石單軸抗壓強度的試驗結果，指出了強度隨尺寸增加而呈冪律衰減規律。

(2) 巖石抗壓強度通常是用材料內缺陷的統計分布來解釋，即巖石是礦物顆粒的集合體，內部含有不同尺度的微缺陷，尺寸愈大的巖石其內部所含微缺陷的概率也愈大，因而其強度愈小。由于本文所有的巖體試件不存在肉眼可見裂隙與缺陷，因此，可對其尺寸效應乾地以下探討。

巖體抗壓強度隨高徑比的變化如圖6所示。從圖6可以看出：無論是貧礦還是白云石大理巖，當巖體高徑比較小時，巖體的抗壓強度較小；當巖體的高徑比較大時，其抗壓強度隨之增大。朱珍德等[9]提出的巖石單軸抗壓強度與高徑比的經驗公式為：

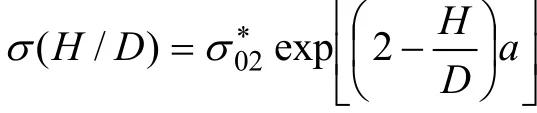
式中：σ(H/D)為任意高度H和直徑D的試樣的單軸抗壓強度；是高徑比為2時試樣的單軸抗壓強度；a為待定系數，與巖性和試驗條件等有關，本試驗中，貧礦a=-0.485，白云石大理巖a=-0.791。再對2組巖樣分別進行模擬計算，得出不同高徑比的單軸抗壓強度如表2和表3所示。

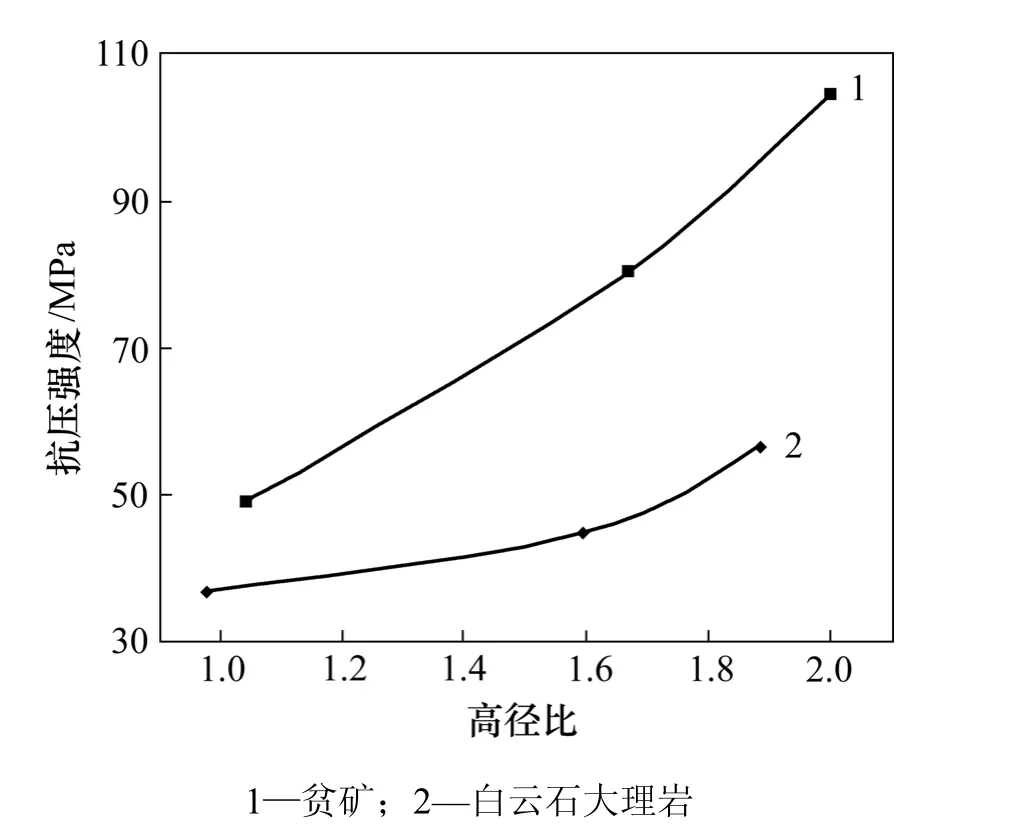
圖6 2組巖樣的抗壓強度與高徑比的關系Fig.6 Relationship between two kinds of rocks’ compressive strength and ratio of height to diameter

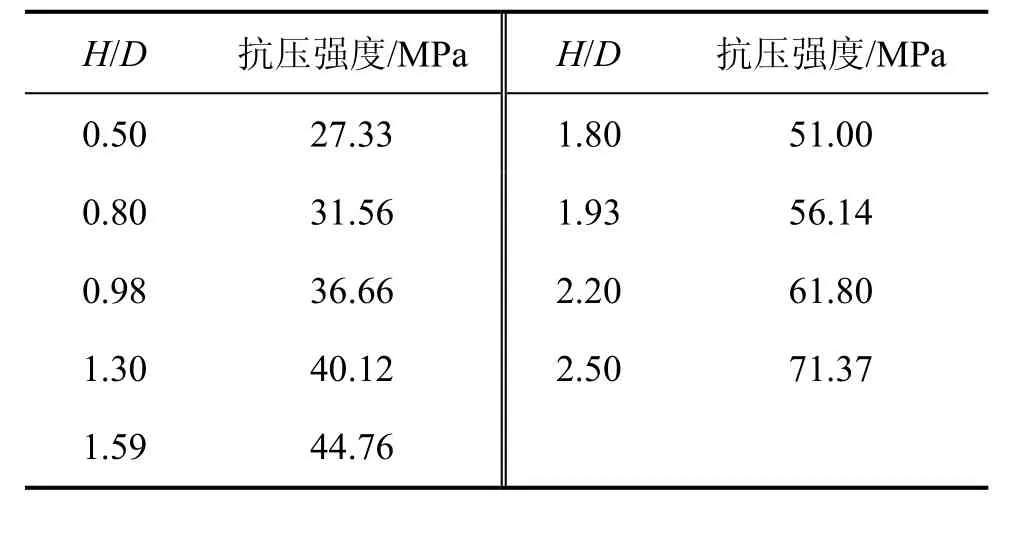
表2 不同高徑比時貧礦的抗壓強度Table 2 Compressive strength of lean ore with different ratios of height to diameter

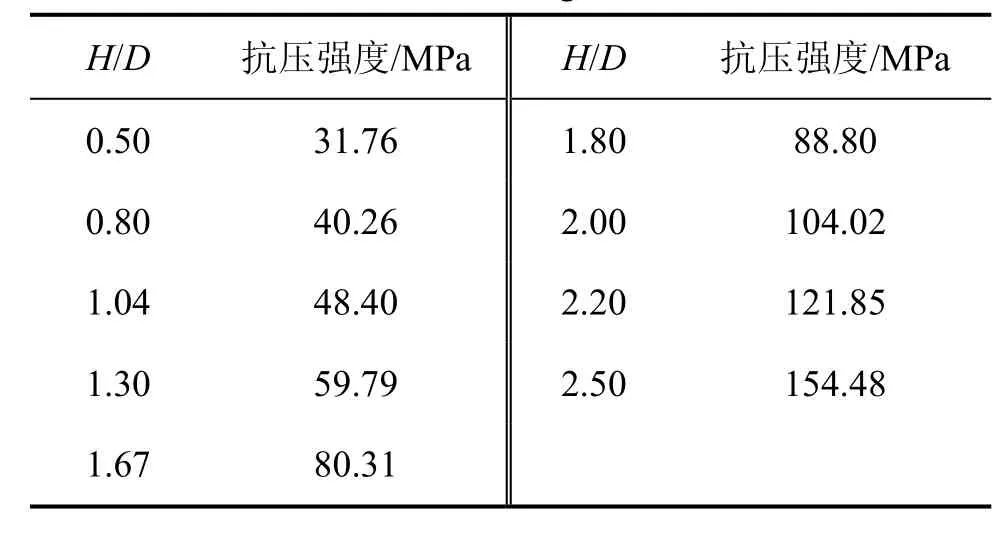
表3 不同高徑比時白云石大理巖的抗壓強度Table 3 Compressive strength of dolomite marble with different ratios of height to diameter

2組巖樣的模擬抗壓強度與高徑比的關系如圖 7所示。可以看出：抗壓強度隨巖體試件高徑比增大而增大的趨勢很明顯，并且呈非線性規律增長。

巖石強度的尺寸效應并不是指具體2個大小不同巖樣的強度差異，也不能簡單地解釋為巖樣尺度越小則所含的缺陷越少, 因而強度增大。巖石材料變形尺寸效應是綜合的平均效應[16]。這里存在2方面的因素：一方面，同直徑不同高度的巖體試件，如果高度增加，巖樣中微缺陷出現的概率將增加，從而導致巖石的彈性模量減小；另一方面，由于端面摩擦效應的作用，隨著巖樣高徑比的增大，試件中間部分脫離三維壓縮狀態，處于單軸壓縮狀態，巖樣內部應力分布將變得更加均勻，從而增加了巖樣的彈性模量[17]。對于本文所用到的試件，由于巖樣端面摩擦效應而導致內部應力分布的均勻性占據主導地位，因而其彈性模量逐漸增加。但如果微缺陷出現概率對彈性模量的影響超過端面摩擦效應的影響，則巖樣的彈性模量將逐漸減小，同直徑不同高度巖樣的試驗結果[3]驗證了這一點。因此，在工程設計時，利用小尺度巖樣強度的平均值作為大尺度構件內各處的強度是不合適的。這實際上假設了材料是完全均勻一致, 造成結構偏于不安全。

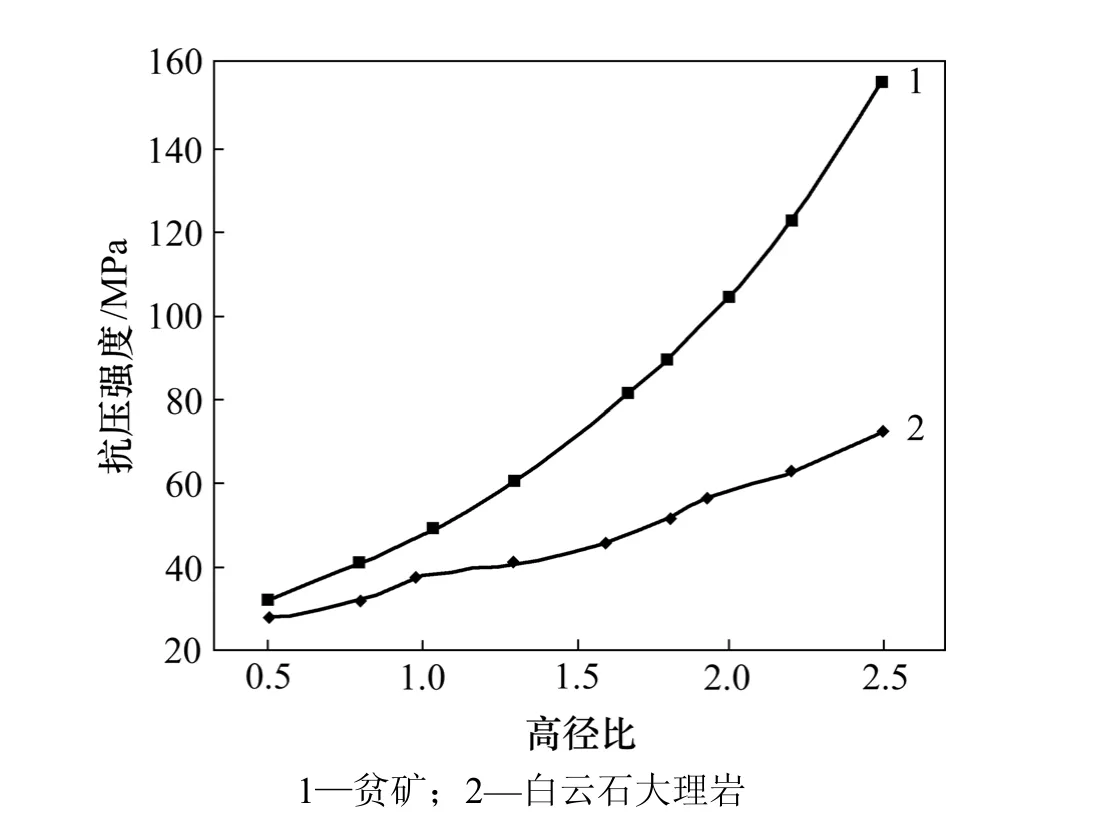
圖7 2組巖樣的模擬抗壓強度與高徑比的關系Fig.7 Relationship between simulation compressive strength and ratio of height to diameter of two kinds of rocks

5 結論

(1) 巖石應力-應變關系曲線的曲率隨著高徑比的增大而增大，隨著高徑比的減小而減小。

(2) 當巖樣高徑比較小時，其彈性模量和極限變形較小；當高徑比較大時，其彈性模量和極限變形則相應增大。

(3) 當巖樣高度較小時，巖樣受到三維壓縮應力區的影響，破壞形式較為復雜；高度越大的巖樣中部應力區接近一維應力狀態，巖石呈劈裂和剪切破壞。

(4) 巖樣抗壓強度隨高徑比的增大而增大。

(5) 尺寸效應是巖石材料本身固有特性。盡管目前對巖石強度尺寸效應的研究已取得一定進展，但由于巖石材料具有非均質性、各向異性、不連續性等特點,再加上工程巖體地質環境和條件復雜，巖石強度尺寸效應仍有待進一步研究。

[1] 王文星. 巖石力學[M]. 長沙: 中南大學出版社, 2004: 5-12.WANG Wen-xing. Rock mechanics[M]. Changsha: Central South University Press, 2004: 5-12.

[2] Hudson J A, Crouch S. Soft, stiff and servo-controlled testing machines[J]. Eng Geol, 1972, 6(3): 155-189.

[3] 劉寶琛, 張寄生, 杜奇中, 等. 巖石抗壓強度的尺寸效應[J].巖石力學與工程學報, 1998, 17(6): 611-614.LIU Bao-chen, ZHANG Ji-sheng, DU Qi-zhong, et al. A study of size effect for compression strength of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(6): 611-614.

[4] 楊圣奇. 巖石材料的非均質性與力學特性的研究[D]. 焦作:焦作工學院, 2003: 58-67.YANG Sheng-qi. The heterogeneity and mechanical properties of rock material[D]. Jiaozuo: Jiaozuo Institute of Technology,2003: 58-67.

[5] 何滿潮, 薛廷河, 彭延飛. 工程巖體力學參數確定方法的研究[J]. 巖石力學與工程學報, 2001, 20(2): 225-229.HE Man-chao, XUE Ting-he, PENG Yan-fei. A new way of determining mechanical parameters of engineering rock masses[J]. Chinese Journal of Rock Mechanics and Engineering,2001, 20(2): 225-229.

[6] 周火明, 盛謙, 鄔愛清. 三峽工程永久船閘邊坡巖體宏觀力學參數的尺寸效應研究[J]. 巖石力學與工程學報, 2001, 20(5):661-664.ZHOU Huo-ming, SHENG Qian, WU Ai-qing. Size effect analysis of macro-mechanics parameters for the rock masses of the TGP ship lock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(5): 661-664.

[7] 王學濱, 潘一山, 宋維源. 巖石試件尺寸效應的塑性剪切應變梯度模型[J]. 巖土工程學報, 2001, 23(6): 711-713.WANG Xue-bin, PAN Yi-shan, SONG Wei-yuan. The model of plastic shear strain grandient on size effect in uniaxial compression of rock specimens[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(6): 711-713.

[8] 尤明慶, 華安增. 巖樣單軸壓縮的尺度效應和礦柱支承性能[J]. 煤炭學報, 1997, 22(1): 37-41.YOU Ming-qing, HUA An-zeng. The size effect of uniaxial compression of rock specimen and support capacity of ore pillar[J]. Journal of China Coal Society, 1997, 22(1): 37-41.

[9] 朱珍德, 邢福東, 王軍, 等. 基于灰色理論的脆性巖石抗壓強度尺寸效應試驗研究[J]. 巖土力學, 2004, 25(8): 1234-1238.ZHU Zhen-de, XING Fu-dong, WANG Jun, et al. Experimental study on size effect on compression strength of brittle rock based on grey theory[J]. Rock and Soil Mechanics, 2004, 25(8):1234-1238.

[10] 李宏, 朱浮聲, 王泳嘉, 等. 巖石統計細觀損傷與局部弱化失穩的尺寸效應[J]. 巖石力學與工程學報, 1999, 18(1): 28-32.LI Hong, ZHU Fu-sheng, WANG Yong-jia, et al. Size effect of statistical mesoscopic damage and local weakening failure of rock[J]. Chinese Journal of Rock Mechanics and Engineering,1999, 18(1): 28-32.

[11] 楊友卿. 巖石強度的損傷力學分析[J]. 巖石力學與工程學報,1999, 18(1): 23-27.YANG You-qing. Continuum damage mechanics analysis of rock strength[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(1): 23-28.

[12] 王學濱, 潘一山, 盛謙, 等. 試件端面效應的變形局部化數值模擬研究[J]. 工程地質學報, 2002, 10(3): 233-236.WANG Xue-bin, PAN Yi-shan, SHENG Qian, et al. Numerical simulation on strain localization of end constraint of rock specimen[J]. Journal of Engineering Geology, 2002, 10(3):233-236.

[13] 肖慶華, 徐衛亞, 巫德斌. 巖石流變力學試驗數據挖掘研究[J]. 工程地質學報, 2004, 12(2): 215-220.XIAO Qing-hua, XU Wei-ya, WU De-bin. A data mining case study for the creep test data of argillite[J]. Journal of Engineering Geology, 2004, 12(2): 215-220.

[14] 鄧聚龍. 灰色系統理論的GM模型[J]. 模糊數學, 1985, 5(2):22-32.DENG Ju-long. GM model of grey systems theory[J]. Fuzzy Mathematics, 1985, 5(2): 22-32.

[15] 尤明慶, 蘇承東, 楊圣奇. 巖石動靜態參數間關系的研究[J].焦作工學院報, 2002, 21(6): 413-420.YOU Ming-qing, SU Cheng-dong, YANG Sheng-qi. Study on the relation between the dynamic and static parameters of rocks[J]. Journal of Jiaozuo Institute of Technology, 2002, 21(6):413-420.

[16] 楊超, 崔新民, 徐水平. 軟巖應變軟化數值模型的建立與研究[J]. 巖土力學, 2002, 23(6): 695-701.YANG Chao, CUI Xin-min, XU Shui-ping. Establishment and study of strain-softening numerical constitutive model for soft rock[J]. Rock and Soil Mechanics, 2002, 23(6): 695-701.

[17] 王國民. 軟質粉砂巖變形與強度的試驗分析[J]. 巖土力學,2000, 21(4): 340-342.WANG Guo-min. Experimental study on deformability and strength of soft siltstone[J]. Rock and Soil Mechanics, 2000,21(4): 340-342.