揚聲器對低頻短純音信號響應的研究

張平柯

(湖南第一師范學院 數學物理系，湖南 長沙，410002)

人們通常采用機電類比法對揚聲器進行定量研究[1-4]，將揚聲器振動系統等效為交流電路，將振動系統元件特性參數等效為電路元件特性參數，將振動系統的狀態參量等效為電路的狀態參量。這種方法的優點在于人們可以利用交變電路系統化的研究成果，研究揚聲器的振動情況，得出聲壓頻率特性、平均聲功率等反映揚聲器及其系統穩態特性的技術指標。由于一般音樂信號中存在大量的猝發性信號，因此，揚聲器系統的穩態技術指標并不能全面反映其對音樂信號的響應，短純音信號較接近真實音樂信號，揚聲器對短純音信號的響應能更客觀地反映其性能[5]。在短純音電信號的驅動下，由于揚聲器的固有特性不可避免地會在振動的啟動階段(前沿)和結束階段(后沿)產生瞬態失真。分析揚聲器對短純音信號的響應有助于提高揚聲器系統的電聲還原質量。機電類比法不太適用于對揚聲器紙盆運動的瞬態分析，為此，本文作者通過求解在短純音信號驅動下揚聲器紙盆運動的微分方程，并利用 MAPLE 軟件[6]代入已知參數繪制響應曲線，同時進行實際測量，將測量結果與理論研究結果進行對照，以尋找影響揚聲器瞬態特性的因素。

1 在短純音信號驅動下紙盆運動微分方程及其求解

在正弦驅動力下工作的揚聲器是一個受迫振動系統，它所受到的驅動力是罐形磁場對音圈施加的安培力，設揚聲器受到的驅動電壓為 U = UMs in (pt)(其中：UM為驅動電壓幅值；p為驅動電壓的圓頻率；t為時間)，當音圈在罐形磁場的均勻區域振動時，該力可表示為 f =BLUMsin (p t)/R (其中：B為罐形磁場的磁感應強度；L為音圈繞線的總長度；R為音圈的直流電阻)。

紙盆運動時受到的阻力由2部分組成：一部分是機械阻力，它主要由空氣阻力形成，在速度不太大的情況下，阻力與速度成正比，即(其中，γ為機械阻力系數)；另一部分是音圈受到的電磁阻力，它可以表示為： 其中， 為電阻力系數)。因此，紙盆受到的總阻力為

設揚聲器的等效振動質量為m，揚聲器振動系統的勁度系數為κ，紙盆離開平衡位置的位移為 x，根據牛頓第二定律，有：

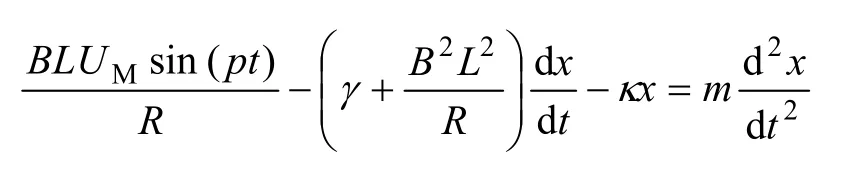
若令驅動力幅 F0=BLUM/R ，總阻力系數χ=γ+B2L2/R ，則揚聲器的振動微分方程為：

式(2)和(3)右邊前面部分對揚聲器起始階段的瞬態特性影響很大，但經歷充分長時間后，都將變成0。最后一項形式相同，引入：

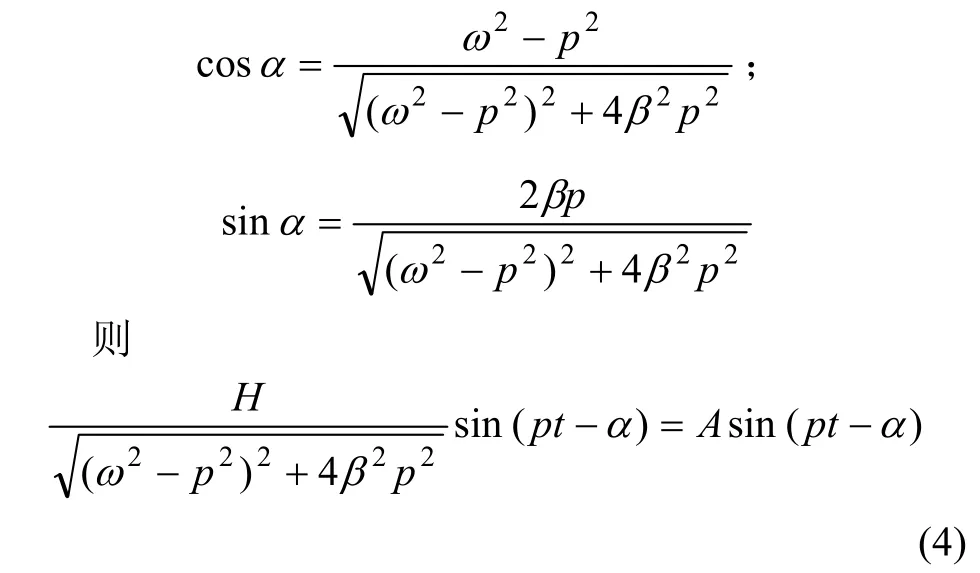
即經歷充分長時間后，揚聲器將作與驅動力頻率相同的運動，但它們間存在相位差-α。也就是說，在t= n(n為整數)時撤除驅動力，揚聲器的振1動位移、速度并不會回到初始狀態。這時，它具有由速度和位移決定的動能和勢能，還將產生余振。其振動方程為典型的阻尼振動方程：

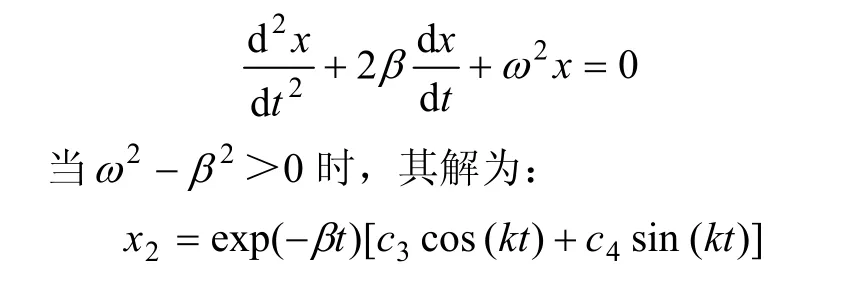
x2決定了揚聲器停振過程中的瞬態特性。其中：c3和c4由x和v在t1時刻的值xt1和vt1來決定，可解得：c3=xt1；c4=(vt1+βxt1)/k。

若將x2的時間起點放到與驅動力相同的時間起點上，則有：

因此，當 ω2- β2＜0時，在短純音信號驅動下，揚聲器紙盆位移可用如下分段函數表示：

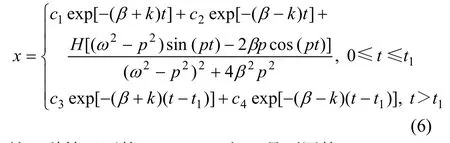
這2種情況下的c1，c2，c3和c4是不同的。

ω2- β2=0的情況可從前2種情況逼近求解。

2 揚聲器對短純音信號響應的分析

對揚聲器來說，人們關心的是它在聆聽位置上的聲壓特性。而聲壓vfaP··=(其中，f為頻率，v為揚聲器紙盆振動速度，a為比例系數)，因此，人們更關心的是揚聲器紙盆的速度。將式(5)和(6)對時間求導，可得紙盆的瞬時速度。

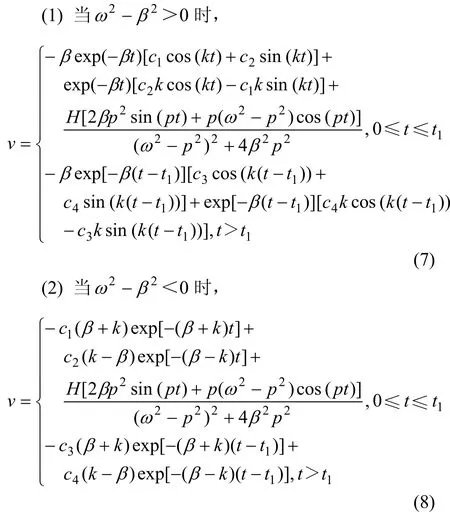
下面分析1只口徑為200 mm的低音揚聲器對低頻短純音信號的響應情況。

實測該揚聲器音圈直流電阻 R=7 Ω，諧振頻率f0=38 Hz，總品質因素Qt=0.73[9-10]。根據振動理論，=163.5，它比ω=2πf0小，應該用式(7)進行分析；H與驅動電壓有關，是一個可以改變的量，因此，可任選。利用MAPLE10作出f=f0=38 Hz時紙盆在0～0.45 s內振動的v-t曲線，如圖1所示。

從圖1可見：第1個速度峰的高度與穩定后的速度峰高度之比約為0.60，而非理想值1.00；余振峰與穩定速度峰的比值約為0.47，而非理想值0。

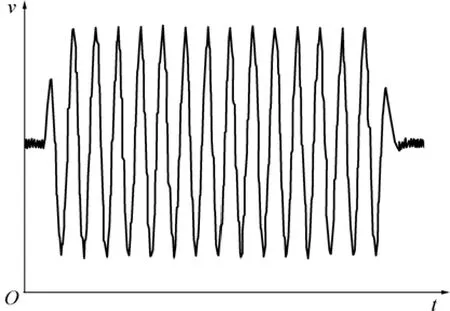
圖2 f=f0時揚聲器紙盆振動的實測v-t曲線Fig.2 Measured v-t curve of cone vibration when f=f0

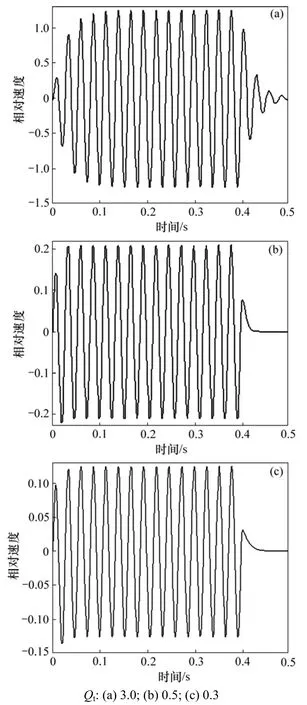
圖3 Qt對38 Hz的短純音信號的瞬態響應的影響Fig.3 Influence of Qt on transient response of 38 Hz tone burst signal

3 揚聲器對短純音信號響應的實測

在進一步分析揚聲器的前、后沿特性與Qt的關系之前，先通過實驗測出紙盆的速度-時間圖像，以確定計算結果與實際情況的符合程度。

通常用麥克風檢測揚聲器的近場聲壓，并借助音頻分析軟件進行分析。但采用這種方法精度很難達到要求。實驗用的揚聲器是一種雙音圈揚聲器，其設計目的在于可靈活變換阻抗適合不同場合應用。將短純音電信號加到1個音圈上，驅動紙盆振動，在另一個音圈上就會因為電磁感應而產生與紙盆的振動速度成正比的感應電動勢E=BLv(其中：B為磁感應強度；L為線圈繞線總長度)。因此，通過計算機分析E的時間變化規律就可以發現速度的時間變化規律，描繪出紙盆振動的v-t圖像。

圖2所示是用該方法測得的實驗揚聲器在f=f0=38 Hz的短純音信號驅動下的v-t曲線。

根據圖2求得第1個速度峰的高度與穩定后速度峰高度之比約為0.59，第1個余振速度峰與穩定速度峰的比值約為0.47，測量結果與理論結果相吻合。

改變短純音信號的頻率，將測量結果與計算機模擬所得結果相比較，發現兩者都很一致。

4 Qt對瞬態特性和聲壓頻率特性的影響

設揚聲器的諧振頻率f0=38 Hz。通過計算機模擬研究不同頻率的短純音信號驅動下的紙盆v-t曲線。

圖 3～5所示分別是驅動信號頻率 f為 38，25和75 Hz時的一組紙盆v-t曲線。從圖3～5可以看出：只要驅動信號的頻率在一定范圍內，Qt越小，揚聲器對短純音信號的前、后沿響應越好。但Qt過小會使聲壓頻率特性劣化。圖6所示是根據vfaP··=用計算機模擬的f0=38 Hz的揚聲器在不同Qt時的聲壓頻率特性。

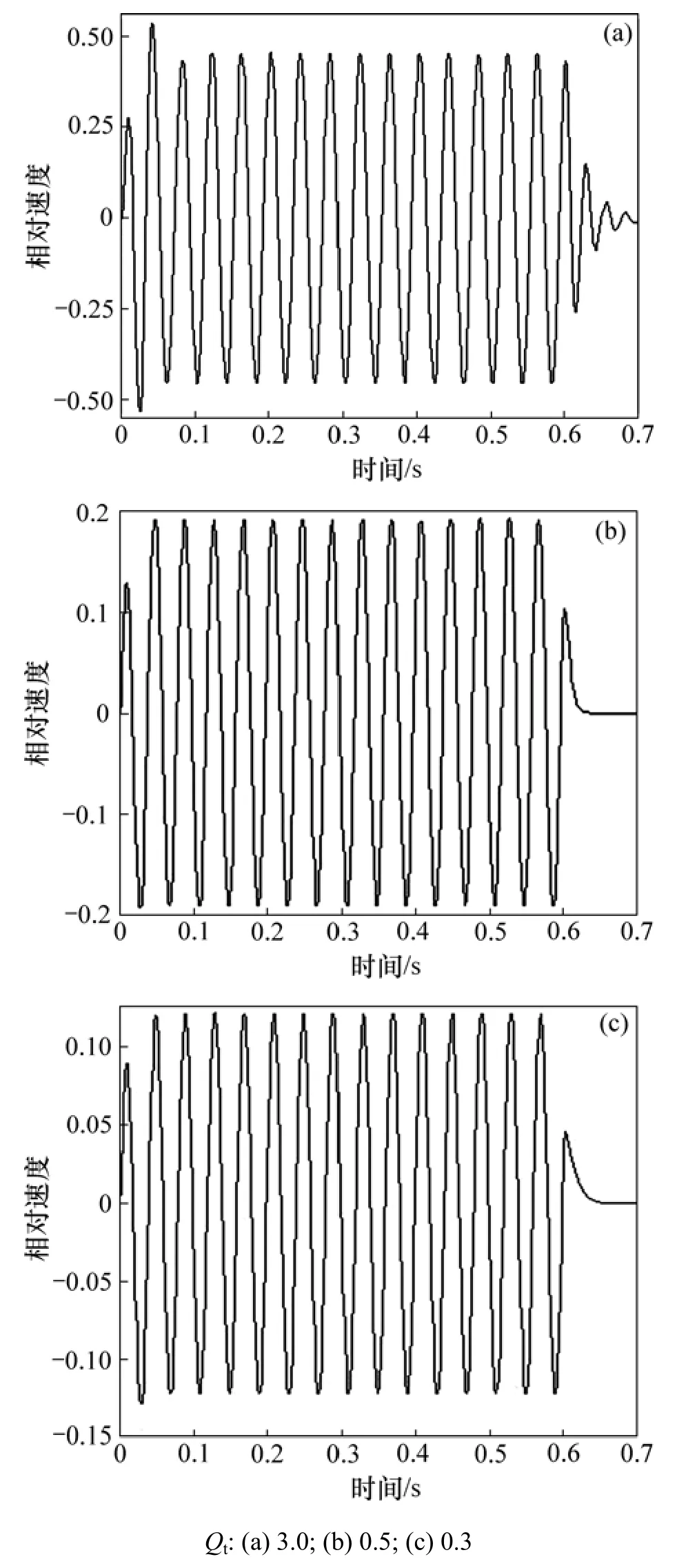
圖4 Qt對25 Hz的短純音信號的瞬態響應的影響Fig.4 Influence of Qt on transient response of 25 Hz tone burst signal

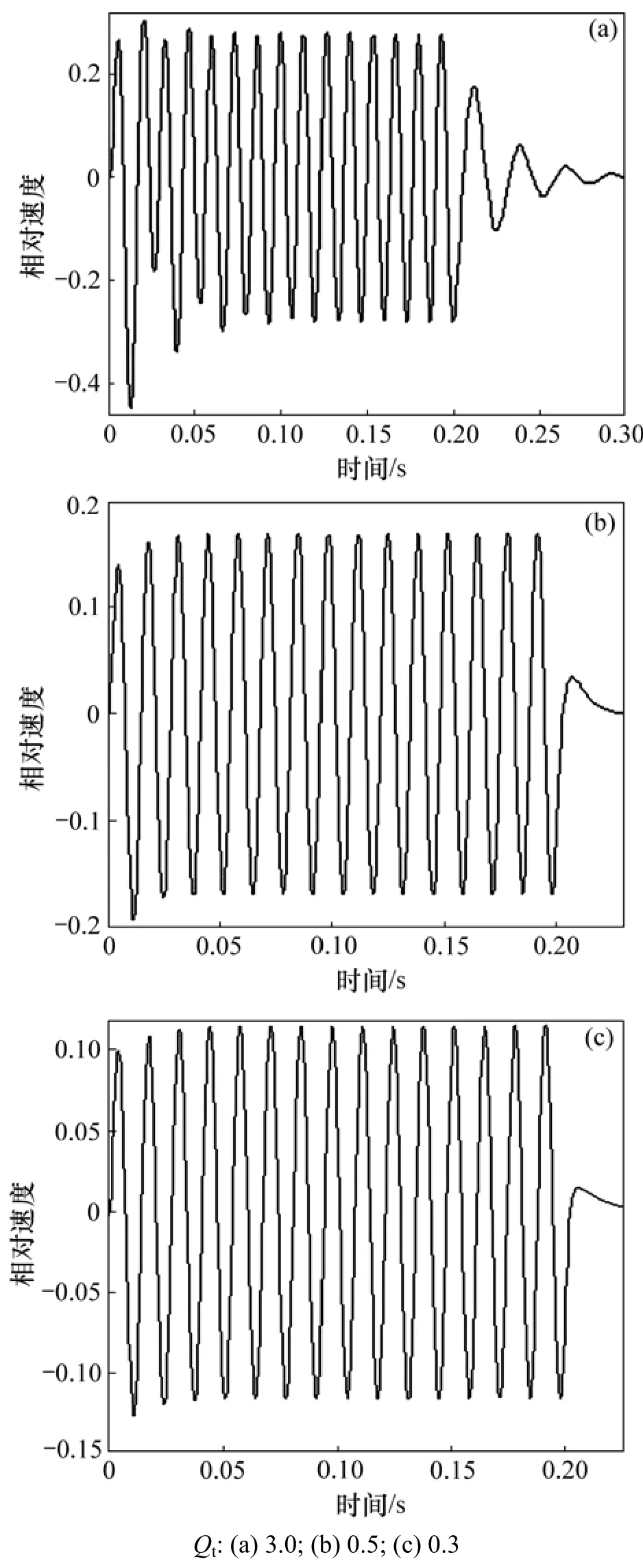
圖5 Qt對75 Hz的短純音信號的瞬態響應的影響Fig.5 Influence of Qt on transient response of 75 Hz tone burst signal

從圖6可以看出：Qt=0.707的揚聲器的聲壓頻率特性最平坦，這與文獻[11]中的結論是一致的。

但從圖1和圖2可以看出：此時揚聲器的瞬態特性并不是很理想，反之，當Qt很小時，雖然揚聲器對單一頻率的短純音信號瞬態響應較好，但聲壓頻率特性很差，低音放不出來。因此，揚聲器的瞬態特性與聲壓頻率特性之間存在不可調和的矛盾。經折中考慮，Qt取0.5～0.7可以獲得良好的綜合性能。

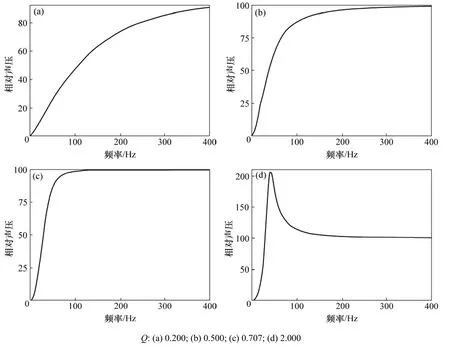
圖6 Qt對聲壓頻率特性的影響Fig.6 Influence of Qt on pressure-frequency characteristics

5 揚聲器的Qm與Qe的等效性

葉希鵬等[12-13]認為：揚聲器的機械品質因素 Qm主要影響其前沿響應，為保證揚聲器的良好的前沿響應，Qm應該比較大。揚聲器的電品質因素 Qe主要影響其后沿響應，為保證揚聲器的良好的后沿響應，Qe應該比較小。

本文作者對這種“Qm與 Qe對揚聲器前、后沿特性具有不同影響”的觀點存在疑問。從前面的討論可知：總阻力系數為機械阻力系數與電阻力系數之和。從對總阻力系數χ的貢獻來看，γ與B2L2/R是等價的，它們任何一個增大都將導致χ增大，從而導致 Qt減小。而Qt的變化總是同時影響系統的前沿特性和后沿特性。為了證實這一點，在實驗揚聲器上串聯2 kΩ的電阻，這時可認為系統的 Qe已經變為原來的 287倍(2007/7)，根據 Qm與 Qe的并聯關系[14-15]，可不考慮Qe的影響，即可認為Qt=Qm(更嚴格地講，應該將R=7 Ω 和 Rg=2 kΩ 代入得到Qt=Qm的結論)。利用前述的測試方法，可獲得揚聲器在f=f0時的紙盆振動v-t曲線，見圖7。

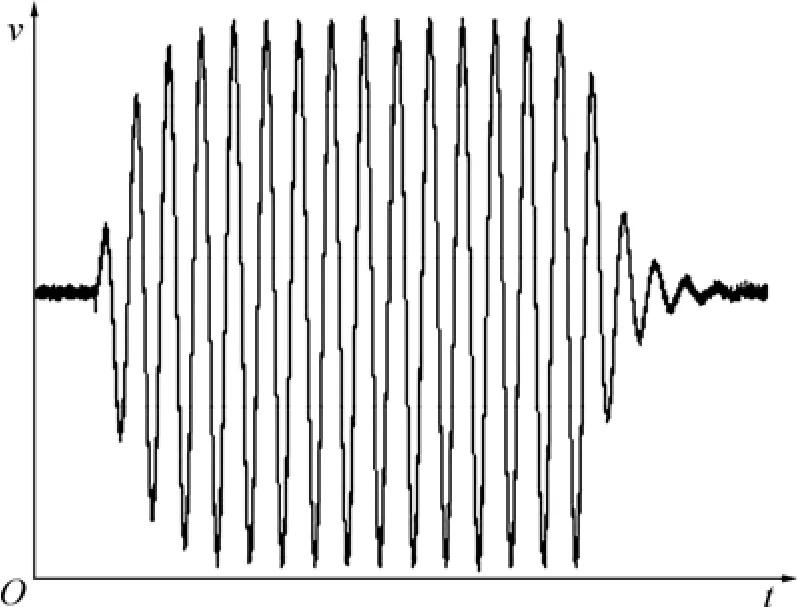
圖7 消除電阻尼影響后揚聲器紙盆的v-t曲線Fig.7 v-t curve of cone after elimination of electrical damping implication

比較圖7和圖2可見：雖然Qm沒有變化，只是Qe產生了變化(更嚴格地說是 Qt產生了變化)，但 Qe變化影響的不僅是后沿特性，而且包括前沿特性。

用嘗試法，通過計算機模擬，發現當系統的 Qt取3時，所得到的圖像與實驗所測得的圖像高度相似(見圖3)，這表明此時系統的Qm=3。圖7與圖3(a)所示的v-t曲線的相似性也表明前后沿特性的變化并不能反映到底是Qm還是Qe發生了變化。換句話說，Qm和Qe對揚聲器的前、后沿特性產生的影響等效，真正影響揚聲器前、后沿特性的是Qt，并且揚聲器的前沿特性與后沿特性是相關的，前沿特性好的揚聲器，后沿特性也好；前沿特性差的揚聲器，后沿特性也差。

通過對揚聲器的工作原理進行分析發現：Qm與Qe的形成機制是不一樣的，Qm與Qe對揚聲器的影響也不盡相同。如罐形磁場的磁感應強度B增加，會降低Qe，同時，還會使揚聲器的靈敏度提高，因此，Qe較小的揚聲器其靈敏度一般較高。在揚聲器 Qt一定時，如何搭配 Qm與 Qe需進行研究。但也許正是 Qm與Qe對揚聲器某些技術指標影響不相同，造成了“Qm和 Qe的對揚聲器的前、后沿特性影響也不一樣”的誤解。

6 測量揚聲器Q的一種可能方法

通過前面的分析，提出一種有效測量揚聲器Q的新方法。

首先，用實驗方法獲取揚聲器的紙盆振動的 v-t曲線(在測Qm時應給揚聲器串上1個充分大的電阻)，將它儲存到電腦中作為比較標準。然后，以Qt作為變量，以一定的步進值從小到大或從大到小(步進值越小，測量的精度越高)變化，讓計算機通過式(7)(Qt＞0.5時)或式(8)(Qt＜0.5時)進行循環運算并作圖，利用圖像比較軟件將每次作出的圖與標準圖像進行比較。當比較結果一致(可以設定允許的偏差值)時，終止程序運行，并輸出此時的Qt。

在開發專用的圖像比較軟件時，可利用揚聲器前后沿特性的相關性，將比較重點放在前沿特性上，只需比較第1個速度峰的高度與穩定后速度峰高度之比。

可采用以上同樣的方法對封閉式揚聲器箱進行討論。

7 結論

(1) 分析了揚聲器在低頻短純音信號驅動下的振動情況，給出了描述揚聲器的速度與時間關系的解析式及速度-時間曲線的計算機作圖法，并用實驗證明了這種方法的正確性。

(2) 從理論上分析了機械品質因素 Qm與電品質因素Qe對揚聲器的前后沿特性影響的等效性，指出了揚聲器前后沿特性的相關性。實驗證明真正影響揚聲器前后沿特性的是總品質因素Qt：揚聲器的Qt越小，其前后沿特性就越好，但Qt太小，會導致聲壓頻率特性的嚴重劣化。經綜合考慮，Qt為0.5～0.7較合適(此結論僅對安放在自由空間和無限大障板上的揚聲器有效，如果將揚聲器裝入音箱中，還必須考慮音箱的具體結構確定其Qt)。

(3) 提出了一種測量揚聲器和封閉式揚聲器箱品質因素Q的可能方法。

(4) 由于在高頻時揚聲器紙盆將產生分割振動，因此，本文的結論僅在低頻時成立。

[1] 馬大猷. 現代聲學理論基礎[M]. 北京: 科學出版社, 2004:72-73.

MA Da-you. Basis of modern acoustical theory[M]. Beijing:Science Press, 2004: 72-73.

[2] 杜功煥, 朱哲民, 龔秀芬. 聲學基礎[M]. 南京: 南京大學出版社, 2001: 116-145.

DU Gong-huan, ZHU Zhe-min, GONG Xiu-fen. Acoustic basis[M]. Nanjing: Nanjing University Press, 2001: 116-145.

[3] 王以真. 實用揚聲器技術手冊[M]. 北京: 國防工業出版社,2003: 23-24.

WANG Yi-zhen. Practical speaker technical manual[M]. Beijing:National Defense Industry Press, 2003: 23-24.

[4] 徐光澤. 電聲原理與技術[M]. 北京: 電子工業出版社, 2007:37-39.

XU Guang-ze. Principle and technology of electro-acoustic[M].Beijing: Electronics Industry Press, 2007: 37-39.

[5] 張平柯. 音頻放大器低頻性能的短純音信號評測法研究[J].中南大學學報: 自然科學版, 2008, 39(5): 1068-1074.

ZHANG Ping-ke. Evaluation method of low frequency performance of audio frequency amplifiers by tone burst signals[J]. Journal of Central South University: Science and Technology, 2008, 39(5): 1068-1074.

[6] 黎捷. Maple9.0符號處理及應用[M]. 北京: 科學出版社, 2004:140-144.

LI Jie. Maple9.0 symbol-processing and its applications[M].Beijing: Science Press, 2004: 140-144.

[7] 王柔懷. 常微分方程講義[M]. 北京: 人民教育出版社, 1978:115-122.

WANG Rou-huai. Ordinary differential equations[M]. Beijing:People’s Education Press, 1978: 115-122.

[8] F.S.克勞福德. 波動學(上冊)[M]. 盧鶴紱, 譯. 北京: 科學出版社, 1981: 121-137.

Crawford F S. Waver(Volume 1)[M]. LU He-fu, trans. Beijing:Science Press, 1981: 121-137.

[9] 萬平英. 聲頻測量技術[M]. 北京: 國防工業出版社, 2006:77-83.

WAN Ping-ying. Audio measurement technology[M]. Beijing:National Defense Industry Press, 2006: 77-83.

[10] 王以真, 沈偉星. 音箱研討(三): 揚聲器低頻參數的測試和計算[J]. 電聲技術, 2007, 31(2): 25-29.

WANG Yi-zhen, SHEN Wei-xing. Study and discussion on loudspeakers (Ⅲ): Measurement and calculation of low-frequency parameters of loudspeaker[J]. Audio Engineering,2007, 31(2): 25-29.

[11] 曹水軒, 沙家正. 揚聲器及其系統[M]. 南京: 江蘇科學技術出版社, 1991: 133, 373.

CAO Shui-xuan, SHA Jia-zheng. Speaker and its system[M].Nanjing: Jiangsu Science and Technology Press, 1991: 133, 373.

[12] 葉希鵬. 詳解揚聲器中品質因數 Q值[J]. 電聲技術, 2006,30(8): 26-28.

YE Xi-peng. Analysis of quality factor of loudspeaker[J]. Audio Engineering, 2006, 30(8): 26-28.

[13] 王以真, 沈偉星. 音箱研討(五): 揚聲器的機械 Q 值 Qms[J].電聲技術, 2007, 31(5): 20-24.

WANG Yi-zhen, SHEN Wei-xing. Study and discussion on loudspeakers (Ⅴ): Mechanical quality factor of the loudspeaker[J]. Audio Engineering, 2007, 31(5): 20-24.

[14] 王以真, 沈偉星. 音箱研討(二): 論揚聲器品質因數 Qts[J].電聲技術, 2006, 30(12): 22-26.

WANG Yi-zhen, SHEN Wei-xing. Study and discussion on loudspeakers (Ⅱ): Analysis of quality factor Qtsof loudspeaker[J]. Audio Engineering, 2006, 30(12): 22-26.

[15] 克林格爾. 高保真揚聲器和揚聲器箱[M]. 沈執良, 鐘厚瓊,譯. 北京: 科學普及出版社, 1984: 20.

Klinger. High-fidelity speakers and speaker boxes[M]. SHEN Zhi-liang, ZHONG Hou-qiong, trans. Beijing: Popular Science Press, 1984: 20.