瀝青混凝土心墻壩應力-應變分析
陳 靜,馬妹英,趙秋霜
(1.河北軟件職業技術學院 智能工程系,河北 保定 071000;2.中水北方勘測設計研究院,天津 300322;3.河間市水務局,河北 河間 062450)
1 工程概況
某大(一)型水庫工程,正常蓄水位為739.0 m,總庫容20.45×108 m3。其瀝青心墻壩最大高度為123.00 m,為一級建筑物,地震設防烈度為8度。壩址地形地質條件復雜,壩基覆蓋層厚5.0~9.5 m,巖性為第四系全新統沖積砂卵石、崩積碎石塊。基巖為變質砂巖,強風化帶厚度4.9~7.0 m,弱風化帶厚度2.3~6.0 m,其上巖體中節理裂隙較為發育。壩體斷面如圖1所示。
2 壩體材料本構關系
面板堆石壩應力-應變的合理性取決于堆石材料本構關系,目前多采用鄧肯在1980年提出的計算理論來計算面板堆石壩應力,修改的非線性雙曲線E-B模型。該模型使用簡便,參數確定簡單,并且在參數確定方面積累了許多成熟的經驗。
E-B模型在曲線上任意一點的切線模量如下:
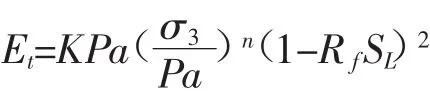
式中:Rf—土體的破壞比
SL—土體單元的應力水平
σ3—圍壓
Pa—大氣壓強
K,n—楊氏模量系數和模量指數
上述公式只適用于荷載逐級增加的情況,當考慮卸荷與重復加載時,土體的應力-應變關系用線彈性模型近似模擬,卸荷再加荷彈性模量。
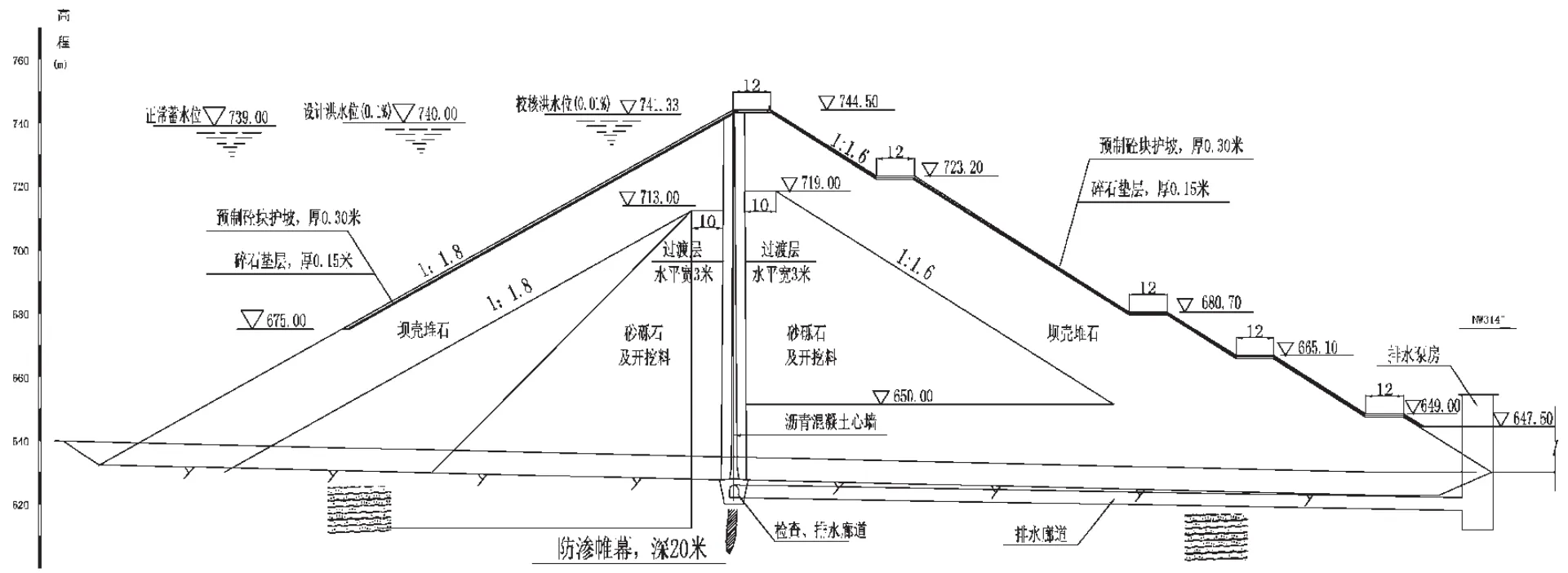
圖1 壩體典型剖面
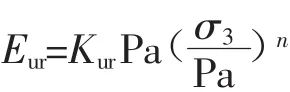
式中:Kur為卸荷模量指數。
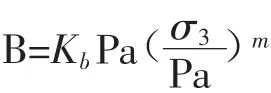
體積變形模量B的關系如下:式中:Kb和m分別為體積模量系數和模量指數。為了使圍壓和應力水平很低的情況下得到的水平應力比較合理,模型中限制最小體積變形模量。
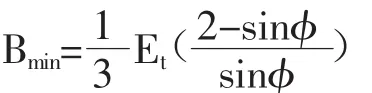
相當于限制最小泊松比
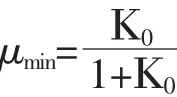
式中:Κ0=1-sinφ
K0為側壓力系數,φ為內摩擦角。
3 計算模型和荷載分級
3.1 有限元計算模型
計算模型如圖2所示,其中坐標系規定如下:順水流方向為X軸,指向下游為正方向;垂直水流方向為Y軸,指向上方為正方向,取壩基面為零點;沿壩軸線方向為Z軸,指向紙面方向為正。
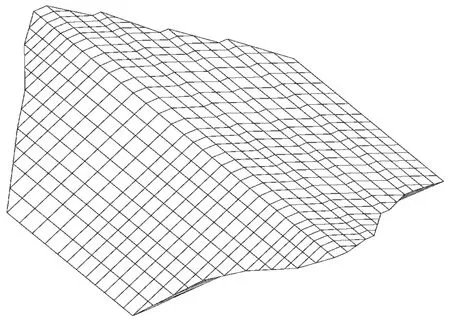
圖2 計算網格圖
3.2 計算參數
壩體堆石料采用鄧肯-張(E-B)模型,計算參數如表1所示。
3.3 荷載分級
模擬壩體填筑過程,計算采用分級加載,使模型單元和材料性質隨時間而改變。考慮壩體施工過程中擋水,即壩體填筑到720 m高程時,壩體開始擋水,擋水高程為650 m,然后直到填筑完成。瀝青心墻作不透水體考慮,水壓力直接作用于心墻上,水位分層逐步抬高。采用三維六面體單元,單元為八節點等參單元,接觸面采用Goodman單元,接縫面采用無厚度和寬度的8節點六面體單元。模型共劃分單元5 188個,壩體分10層填筑,每層厚度約13米。水荷載分6級施加,水位逐步升高到正常蓄水位。浸水單元的重度改為浮重度,計算中混凝土瀝青心墻與過渡料之間未考慮滑移和脫空的發生。
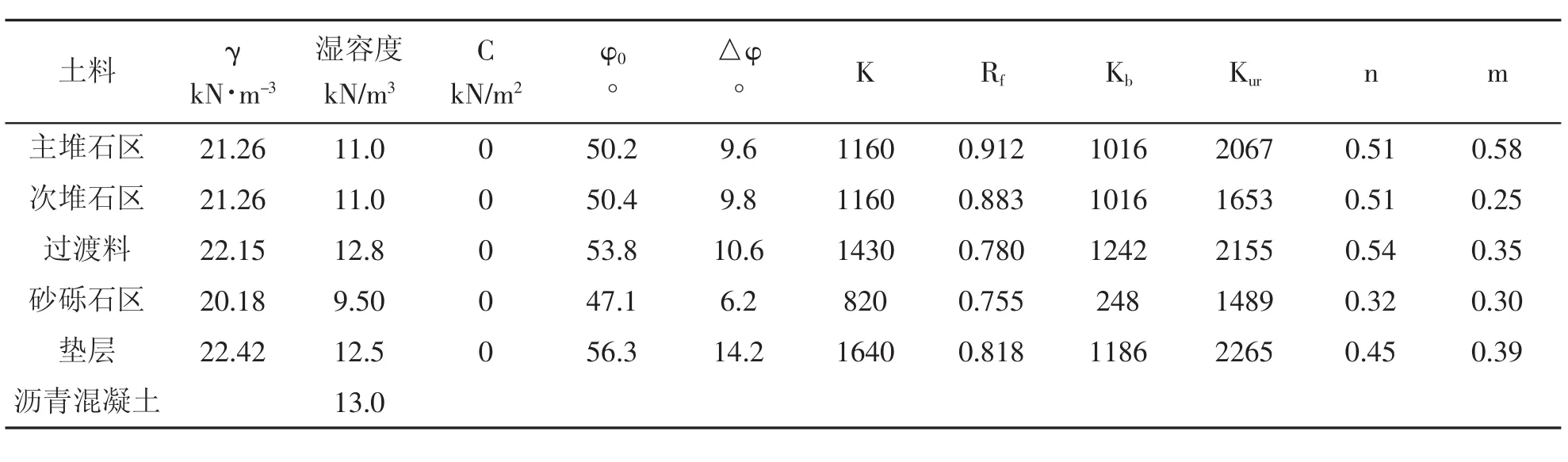
表1 壩體鄧肯-張模型(E-B)參數
4 計算成果
本次僅對竣工和正常蓄水兩種工況中計算剖面的位移、正應力、塑性應變進行了整理,結果如圖3~圖9所示。由結果可以看出:
(1)竣工工況:填筑到720 m高程時,開始擋水至650m,直到填筑完成。最大豎直位移發生在1/2壩高處,值為35.3 cm;最大水平位移發生在上下游坡的1/4壩高處,分別向上游位移6.1 cm、向下游位移7.4 cm;壩體內的垂直應力與填筑高度有關,反映了自重應力的影響,瀝青混凝土心墻底部的應力最大,為2.64 MPa。壩體內沒有出現塑性應變單元。
(2)蓄水工況:混凝土瀝青心墻承受水壓力,下游壩體受壓,整個壩體向下游位移,最大水平位移出現在壩頂,值為29.1 cm;最大垂直位移出現在1/2壩高偏下游側,值為28.9 cm;壩體內的垂直應力上游側較竣工時減小,下游側壓應力增大,最大壓應力出現在下游過渡料底部,值為1.85 MPa;瀝青混凝土心墻底部的垂直應力為0.88 MPa,壓應力大大減小。此工況下發生塑性變形,塑性主要發生在心墻上游側的砂礫料內,最大塑性壓應變達0.004。
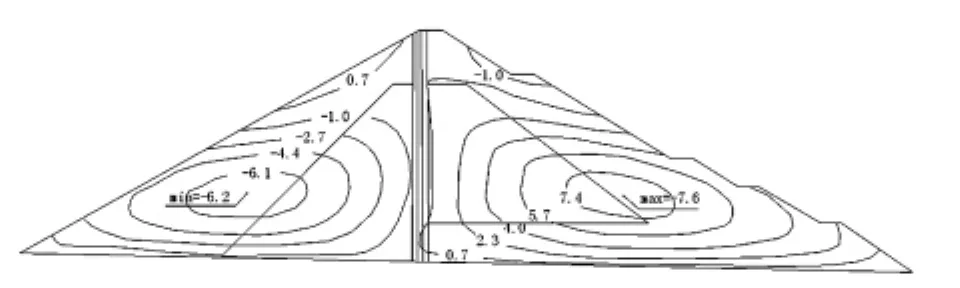
圖3 竣工工況壩體水平位移等值線圖(cm)
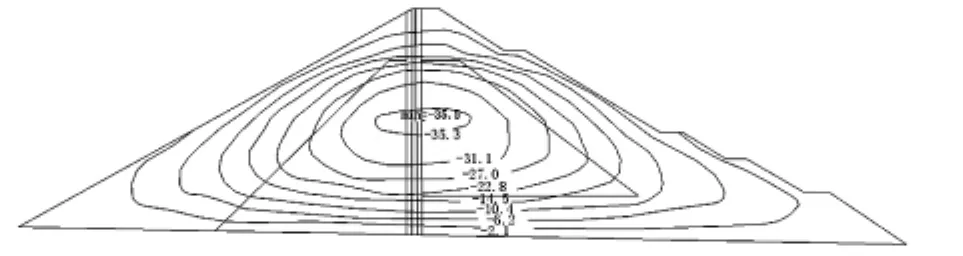
圖4 竣工工況壩體垂直位移等值線圖(cm)
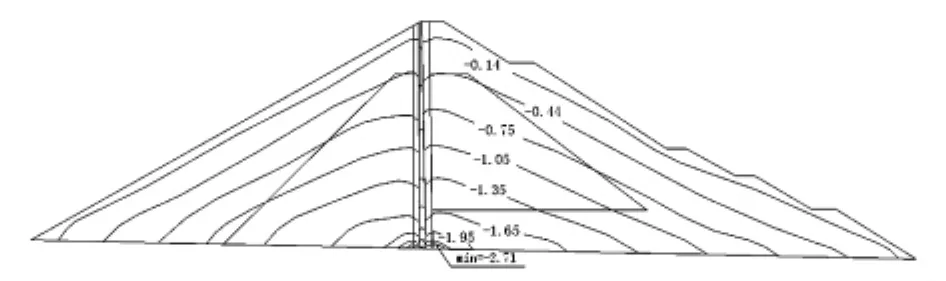
圖5 竣工工況壩體垂直應力等值線圖(cm)
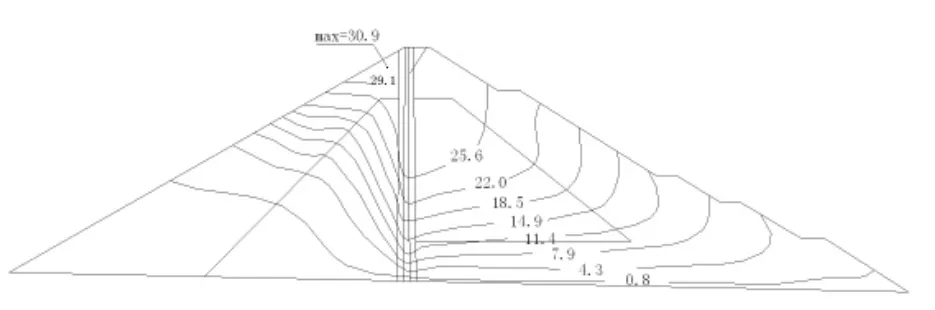
圖6 正常蓄水位時壩體水平位移等值線圖(cm)
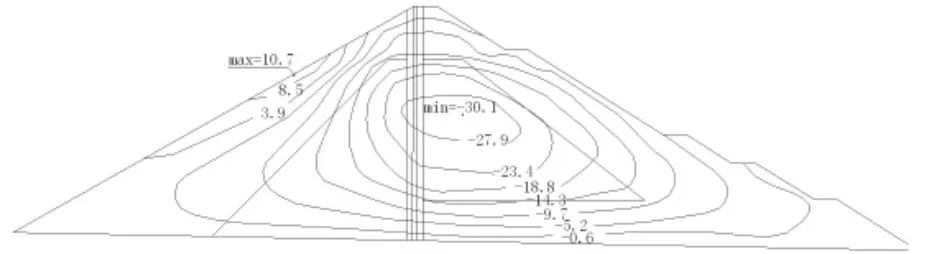
圖7 正常蓄水位時壩體垂直位移等值線圖(cm)
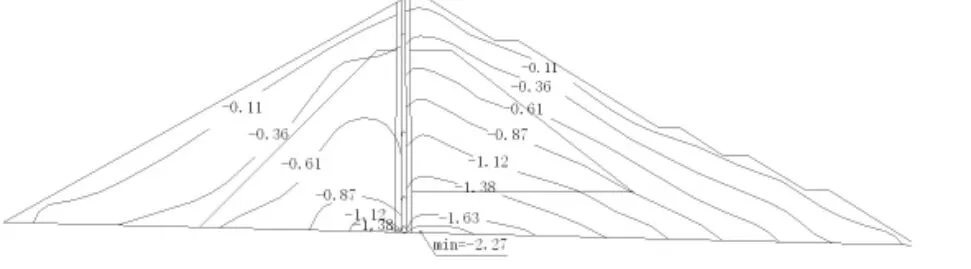
圖8 正常蓄水位時壩體垂直應力等值線圖(cm)
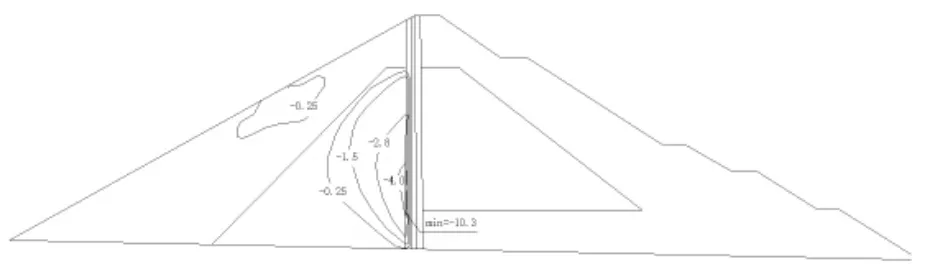
圖9 正常蓄水位時壩體塑性應變等值線圖(cm)
5 結語
(1)壩體填筑過程中,填筑該層的自重由本層及下面已填筑形成的結構承擔,計算出的結點位移是該層填筑形成結點后受上層填筑重量荷載作用下產生的位移,最大垂直位移發生在約1/2高度處,只是蓄水時最大沉降點偏向下游。竣工時水平位移的大值分別發生在上、下游邊坡內,向坡外位移。蓄水后,瀝青混凝土心墻擋水,水平位移均向下游,最大值發生在壩頂。
(2)竣工以后,壩體內的應力分布較均勻,這與填筑高度相關。混凝土瀝青心墻底部的垂直應力最大,壩內無塑性發生。蓄水后,應力發生了很大的變化,混凝土瀝青心墻底部的垂直應力減小,不會產生水力劈裂。上游壩料受水的浮力作用,壓應力減小,壩體內部砂礫料和過渡層產生了塑性應變,最大塑性變形發生在1/6壩高處的過渡層內。壩體內部的塑性應變發生范圍有限,數值不大,不影響壩體穩定。
[1]王勖成,邵敏.有限單元法基本原理和數值方法[M].北京:清華大學出版社,1997.
[2]陳慧遠.土石壩有限元分析[M].南京:河海大學出版社,1987.
[3]SL274-2001.碾壓式土石壩設計規范[S].北京:科學出版社,2001.
[4]關志誠.混凝土面板堆石壩三維非線性有限元應力應變分析[J].東北水利水電,1989(09).

