一種新的克服多普勒頻移的分集算法

吳風麗,鄒衛霞,李 斌,張文碩

(1.濟南鐵道職業技術學院,山東濟南250104;2.北京郵電大學無線網絡實驗室,北京100876)

0 引言

正交頻分復用(OFDM)在無線傳輸中獲得較高的數據傳輸率,因而廣泛應用于IEEE 802.11、IEEE 802.15和IEEE 802.16等標準中。盡管OFDM技術可有效地對抗多徑衰落,卻對同步要求異常嚴格。微小同步偏差將破壞子載波間正交性,致使OFDM系統產生嚴重的子載波間干擾(ICI)。高速運動產生的Doppler頻移將極大惡化系統性能,文獻[1]利用多普勒分集接收機對抗多普勒頻移,分集接收機每條支路首先采用MMSE準則進行信道均衡,然后進行最大比合并,實現復雜度較高。文獻[2]直接優化合并系數,但ICI引起的誤碼率地板效應制約系統性能的提高[3];此外并未考多徑效應對接收機性能產生的影響。為此,本文采用一種全新思路來研究多普勒分集接收機的優化問題,以多普勒頻移引起的損失信噪比為目標函數,對分集接收機中各支路頻移量與合并系數進行聯合優化。在已知最大多普勒頻移情況下,利用Taylor級數將優化目標展開成一個確定函數,最終求得目標函數下的聯合最優解。在降低實現復雜度的同時,算法性能也可逼近MMSE分集接收機。另外,本算法具通用性,不僅適用于克服多普勒頻移,還可用以消除其他任何原因所引起的子載波間干擾。

1 信道模型

在綜合考慮多徑效應和多普勒效應的情況下,多徑時變信道的時間沖激響應為:

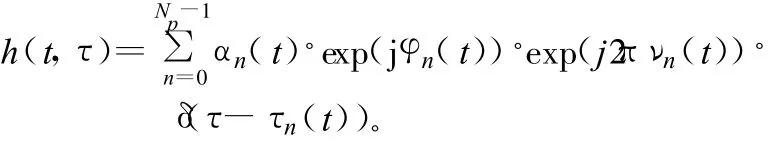
式中,Np為多徑數目;αn(t)、φn(t)、νn(t)和 τn(t)分別為t時刻、第n條路徑的幅度衰減、相位漂移、多普勒頻率擴展和信號的時延。一般地,φn(t)服從均勻分布,αn(t)服從Rayleigh分布。本文分析中,采用多普勒擴展譜為平坦譜[4]。

2 多普勒分集接收機

2.1 頻率偏移對性能影響分析

OFDM信號由N個子載波符號xn構成,假設接收端已準確完成符號同步與樣值同步,且暫不考慮多徑衰落的影響。這時高速運動所產生的多普勒頻移以及接收端振蕩器不穩定引起的頻率漂移將使載波頻率發生偏移,此時接收信號可寫為:

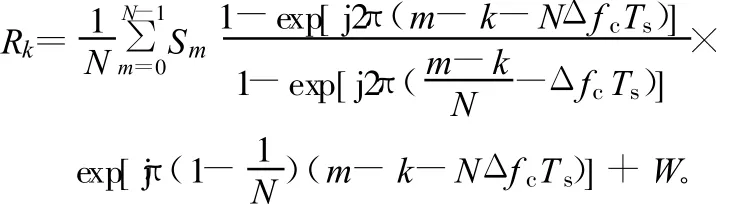
式中,Δfc為載波偏移;Ts為采樣周期;W為加性高斯白噪聲。上式可進一步化簡為:式中,而很明顯,當存在載波偏移時接收信號包括3部分:SkIkk表示發送的數據;為載波偏移所引起的子載波間干擾;W為加性高斯白噪聲分量。

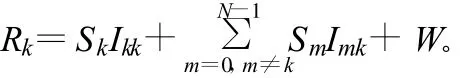
2.2 多普勒接收機

為了降低子載波間干擾,本文采用多普勒分集接收機結構如圖1所示。

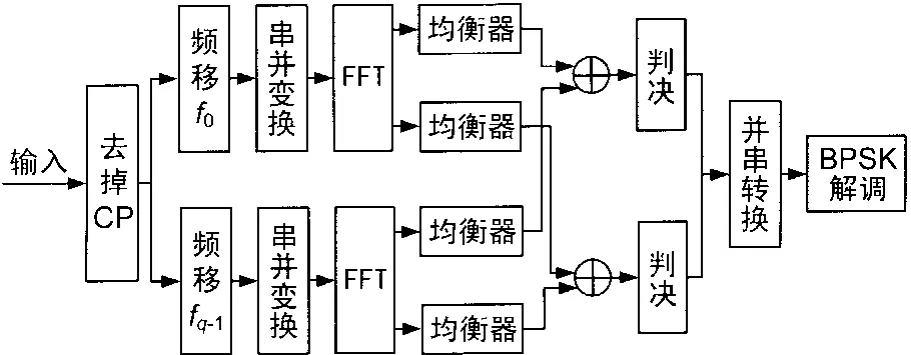
圖1 Doppler接收機結構

接收信號去除循環前綴(CP)后,經由多條頻移支路實現分集接收。每條分集支路先對信號進行頻移,再經串并變換、FFT、LS信道均衡后,將每條支路上所對應的子載波數據分別進行加權合并,最后進行接收判決。其中均衡器用以信道估計和信道均衡,來消除多徑干擾。

3 Doppler分集接收機優化算法

假設分集接收機中各支路頻移為fi,合并系數為αi(i=0,1,…q-1,q為分集接收機的支路數目),則接收信號中有用信號分量為:

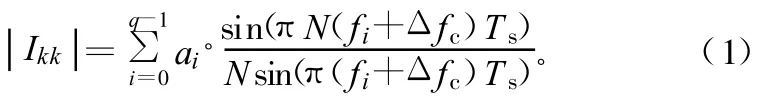
同時,子載波間干擾勢必引起系統性能下降。定義信噪比損失為[5]:

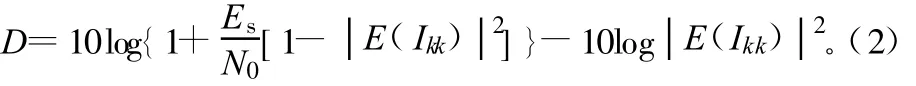
式中,Es/N0為OFDM系統信噪比。載波偏移量Δfc為隨機變量;Ikk亦為隨機變量;E(Ikk)則表示隨機變量Ikk的數學期望。

分集接收主要目的是最大程度地增強有用信號分量,同時抑制子載波間干擾,以減小多普勒頻移所引起的信噪比損失。本文選取頻率偏移所產生的損失信噪比作為算法的目標函數,對多普勒接收機的支路頻移和合并系數為進行聯合優化,使接收信號的信噪比損失最小,從而降低多普勒頻移的影響。

由于平坦譜定義的多普勒擴展 Δfc為在定義域[-FD,FD]上服從均勻分布,以往文獻中對支路頻移與合并系數的優化都比較復雜[3]。考慮到實際無線通信系統中,市區典型的多普勒頻移的最大值約為200 Hz,在高速運動的環境下,可能達到1 kHz[6],而在超高速移動環境中可高達2 kHz。所以,Ikk的分母項可以直接展開成1階Taylor級數:

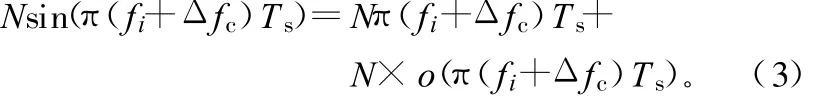
實際系統中N取值較大,因此|Ikk|中分子項可展開成3階Taylor級數:

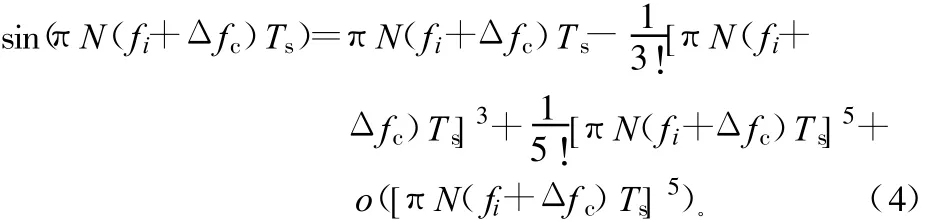
最后E(Ikk)可寫為:

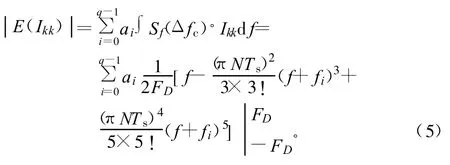
從式(5)中可發現,在無需實時估計多普勒頻移Δfc,得最大多普勒頻移Fd的準確估計值的條件下,即可依據多普勒頻移的概率分布,將式(2)化簡成為一個關于支路頻移fi和合并系數ai的確定函數。求解式(2)最優值等效于求|E(Ikk)|2最大值。考慮信號歸一化處理,本算法將優化支路頻移fi和合并系數ai使得式(6)達到最大值。

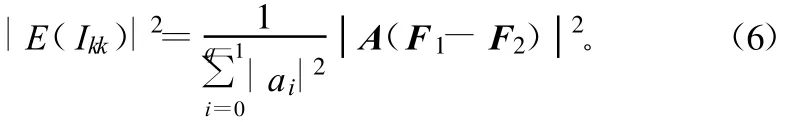
式中,A=[a0a1…aq-1]為1×q維向量,表示分集接收機合并系數;F1和F2表示由分集接收機的頻移向量f=[f0f1…fq-1]1×q和最大多普勒頻移FD生成的q×1維矩陣:

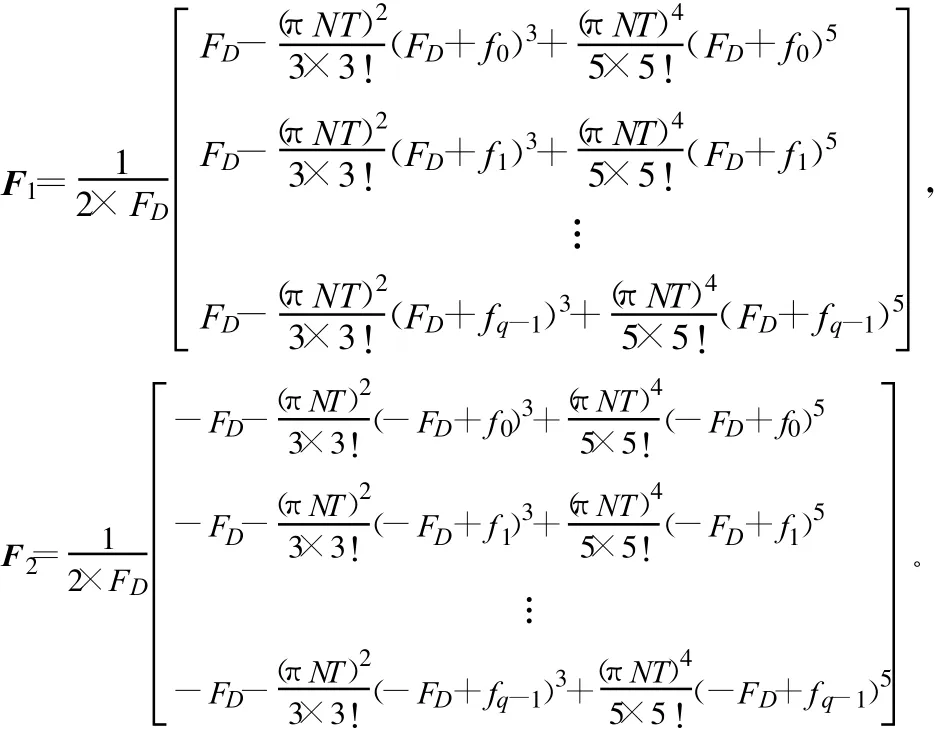
對于式(6)可利用多元函數求條件極值方法進行處理,也可利用數值優化方法(例如最陡下坡算法)來直接得到關于fi和ai聯合最優化解。需注意,由于解曲面上存在局部最小值,因而必須利用蒙特卡羅法隨機選取初始值,最后從中獲得最優解。

4 仿真與性能比較

4.1 算法精度的驗證

利用泰勒公式進行級數展開將產生舍入誤差。對于給定的某個最大多普勒頻移,首先產生10 000個隨機均勻分布的多普勒頻移量,按照式(1)和式(2)計算平均損失信噪比;之后利用式(3)和式(4)中得到的簡化算法,計算得到平均損失信噪比。上述二者之間相對誤差小于3%,因而簡化算法能基本滿足工程要求。

4.2 目標函數中Es/N0的選取

在利用式(6)求解參數的聯合優化解時,需要預先設定OFDM系統信噪比Es/N0的值。但實際的信噪比?Es/N0會隨時間變化,可能會與優化過程中所設定信噪比Es/N0不一致。在低信噪比情況下,信道估計(信噪比估計值)的誤差對系統性能影響很小,故可以忽略。但高信噪比情況下,信道估計差錯卻對系統性能有顯著影響。因此,優化算法中預設Es/N0時選擇高信噪比。

4.3 聯合優化解

為分析方便,多普勒分集接收機采用3條分集支路(q=3),最大多普勒頻移取為Fd=1 800Hz。支路頻移fi和合并系數ai滿足對稱關系,即a0=a2=a,f0=-f2=f。此時,由f、a以及|E(Ikk)|2所構成的三維曲面俯視圖如圖2所示。在該曲面上存在f和a的聯合最優解,使目標函數D達最小值,從而使系統獲得最優分集增益,聯合最優解為:f0=-f2=1 825 Hz,f1=0;a0=a2=-0.16,a1=1。進一步發現 ,損失信噪比D的極值在f和a形成的具特定約束關系的曲線上獲得,對于任意給定的某個最大多普勒頻移,支路頻移和合并系數相互制約。若僅對兩參數之一進行單獨優化,事實上很難獲得最優性能。

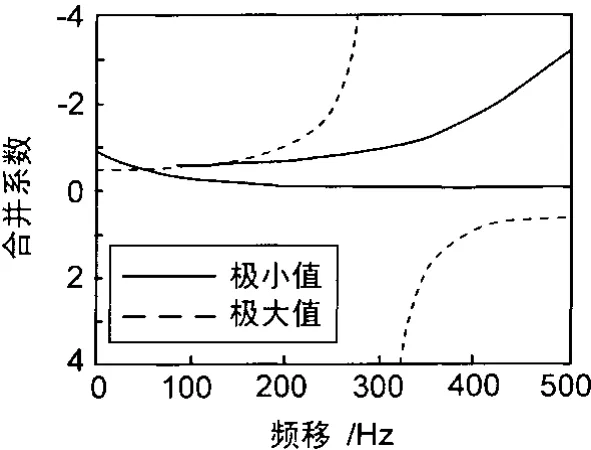
圖2 頻移和合并系數構成的解曲線

4.4 優化算法的性能仿真

假設FdT=0.5,其他系統參數如下設置:OFDM帶寬為16 MHz,符號長度選擇4×10-6s,OFDM符號塊長度6.5×10-5s,FFT點數為64,CP長度為0.8×10-6s,多徑數目為3,采用LS信道估計,Es/N0預設為35 dB,并且仿真中使用了自適應調制方式,可以根據信道特征選擇BPSK、QPSK、16QAM 或64QAM方式。仿真使用了卷積碼編碼,碼率可以在1/2、2/3和3/4之間自適應選擇。仿真得到優化算法的性能曲線如圖3所示。

圖3 優化算法的性能

其中,EC表示多普勒分集接收機采用等增益合并時的性能曲線,此時,僅需對支路頻移進行優化。而OC表示利用本文算法對和進行聯合優化所得到的性能曲線。很明顯,在高信噪比條件下,進行聯合參數優化的Doppler-Rake分集接收機要比等增益Doppler-Rake接收機的性能好的多。

對于文獻[1]中所提的MMSE算法,當分集接收機采用5條支路,每條支路抽頭數為32,信噪比30 dB時仿真可得系統誤碼率為0.002 8。本算法仿真中,選用3條分集支路,且信噪比為30 dB時,系統誤碼率可降至0.002。所以本算法在極大地降低了系統的實現復雜度的情況下,性能也可以逼近MMSE算法。

為了克服載波偏移給OFDM系統的影響,通常先要用復雜的算法對頻移進行實時估計,在此基礎上進行載頻校正,以降低子載波干擾引起的性能下降。本算法則避免了實時估計頻移,僅需獲得頻率偏移的概率分布(例如多普勒頻移一般服從均勻分布,振蕩器不穩定產生的頻移近似服從高斯分布),即可簡化得到優化目標函數,對此函數求極值即可得到分集接收機的最優參數解。

另外本算法具普適性,除了克服多普勒頻移外,對于其他任何原因引起的載波頻率偏移問題,均可用該算法進行分析和解決。假設振蕩器的頻率抖動服從高斯分布,則利用式(5)結合泰勒級數展開就可得到關于支路頻移和合并系數的確定函數表達式,求此函數的極值即可獲得接收機參數的最優解。

5 結束語

在研究多普勒分集接收機的性能優化問題時,考慮了頻移量與合并系數的制約關系,對參數進行聯合優化,利用泰勒級數展開大大簡化了目標函數。在系統采用簡單的LS信道估計的條件下,該算法可以顯著提高系統的誤碼性能,有效地降低由于ICI產生的誤碼率地板效應,且大大降低了實現復雜性。

[1]KIM Byung-Chul,LU I-Tai.Doppler Diversity for OFDM Wireless Mobile Communications:Part I:Frequency Domain Approaches[C].IEEE Vehicular Technology Conference,2003:2677-2681.

[2]WANG Xin,ZHU Gang,CHEN Xia,et al.Doppler Diversity for OFDM High-Speed Mobile Communications[C].IEEE ICC,2006:4665-4669.

[3]STEENDAM H,MOENECLAEY M,SARI H.The Effect of Carrier Phase Jitter on thePerformance ofOrthogonal Frequency-division Multiple-accessSystem[J].IEEE Trans.On Comm.,1998,46(4):456-459.

[4]KAVEH P.Wireless InformationNetworks[M].New York:John Wiley&Sons,1995.

[5]SPETH M,FECHTEL S A,FORK G,et al.Optimum Receiver Design For Wireless Broad-Band Systems UsingOFDM:Part 2[J].IEEE TransOn Comm.,2001,49(4):571-578.

[6]PROAKIS J G.Digital Communication(Fourth Edition)[M].Beijing:Publishing House of Electronic Industry,2006.