FIR數字濾波器的設計與實現

張建偉,展雪梅

(中國電子科技集團公司第五十四研究所,河北石家莊050081)

0 引言

隨著信息時代和數字世界的到來,數字信號處理得到了快速發展,并已廣泛應用于語音、圖像、自動控制、航空、航天、醫療和家用電器等眾多領域。而在數字信號處理領域中,數字濾波器又占據了十分重要的位置,利用所需信號和其他信號在頻譜上的差別,通過數字濾波器可獲得濾除雜波、保持原有信號不變的效果。由于數字濾波器所處理的信號為離散信號,可以用差分方程對其進行描述,用離散變換的方法來分析、處理信號,這樣既有利于數學分析,又可清楚地描述出所設計濾波器的形式。

1 FIR數字濾波器結構特征與設計

1.1 FIR數字濾波器結構特征

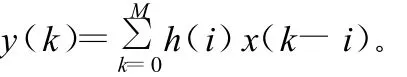
FIR數字濾波器的沖激響應只能延續一定的時間,N階因果有限沖激響應濾波器的差分方程表達式為:其卷積和是一個有限和,可以直接計算y(k),所以其涉及的基本操作就是簡單的乘和加,其計算僅需要所給出的初始樣本值及所要求的相關樣本值。

通過精確設計,有限沖激響應濾波器在整個頻率范圍內均能提供精確的線性相位,由于系統的單位脈沖序列為有限長序列,當輸入有限時,輸出也必然為有限,這樣其穩定性總可以獨立于濾波器系數之外。因此,在很多情況下,有限沖激響應濾波器成為首選,只要確定能滿足要求的轉移序列或者脈沖響應的常數,就可以準確地設計出滿足要求的FIR數字濾波器。通常所采用的設計方法主要有窗函數、頻率采樣法和等波紋最佳逼近法等,其中窗函數法是從時域進行設計的,其算法簡單、物理意義清晰,因此得到了較為廣泛的應用。

1.2 FIR數字濾波器設計

1.2.1 FIR數字濾波器設計步驟

(1)選擇參數

在大多數應用中,需要設計的FIR數字濾波器的幅度或者相位(延時)響應是確定的。在某些情況下,則可能會指定濾波器的單位抽樣響應或者階躍響應。在實際應用中,關鍵的問題是用一個可實現的傳輸函數去逼近給定濾波器幅度響應指標,因此設計一個FIR數字濾波器之前,應首先根據實際需要確定所設計的FIR數字濾波器的技術參數。在頻域中,參數的形式一般是給出幅度和相位響應。幅度參數以絕對參數或者相對參數來給出。絕對參數提供了對幅度響應函數的要求。相對參數以所要求分貝值的形式給出。在工程應用中,多給出相對參數指標。對于相位響應參數形式,通常指的是系統在通頻帶中有線性相位。而運用線性相位響應進行濾波器設計具有如下優點:①只采用實數算法,不涉及復數運算,運算相對簡單;②延遲數量固定,不存在延遲失真;③計算量小,對于長度為N的濾波器(階數為N-1),計算量僅為N/2數量級。

(2)逼近

確定了設計要求的技術參數后,建立一個理想的FIR數字濾波器模型。然后,利用數字濾波器的設計方法,設計出一個實際數字濾波器模型來逼近給定的目標,從而得到所設計的FIR數字濾波器。

(3)性能分析和計算機仿真

通過以上兩步得到的FIR數字濾波器為沖激響應描述的濾波器。根據這個沖激響應就可以分析FIR數字濾波器的頻率特性和相位特性,從而驗證設計結果是否滿足指標要求;或者利用計算機仿真,對設計的FIR數字濾波器進行分析,并根據仿真結果對FIR數字濾波器進行判斷。

1.2.2 利用MATLAB設計FIR數字濾波器

在MATLAB進行線性相位FIR數字濾波器設計中,多采用窗函數法。窗函數法設計FIR濾波器的基本思想是:根據需要設計的濾波器技術指標,選擇合適的濾波器長度N和窗函數ω(n),使通過窗函數的波形具有最窄寬度的主瓣和最小的旁瓣。其核心是根據給定的頻率特性,通過加窗的方式來確定有限長單位脈沖響應序列h(n)。在實際應用中,通常采用的窗函數有以下幾種,即矩形窗、巴特利(Bartlett)窗、漢寧(Hanning)窗、漢明(Hamming)窗、布萊克曼(Blackman)窗和凱塞(Kaiser)窗。

根據工程需要進行實際的FIR數字濾波器設計,要考慮多方面要求,選擇合適的窗函數,并結合計算機仿真對所得到FIR數字濾波器進行分析。在實際設計過程中,所要求的FIR數字濾波器指標為:fn=[1 350,1 825,2 825,3 500],a=[0,1,0],dev=[0.000 5,0.00 5,0.000 5],阻帶最小衰減為65 dB,采樣頻率為10 kHz,則根據阻帶最小衰減來選擇凱塞窗,利用MATLAB的求階函數和FIR數字濾波器的設計函數,其調用的參數格式為:h=fir1(N,ωn,window,′type′),其中,N,ωn分別為 FIR 數字濾波器階數和歸一化3 dB截至頻率,window為窗序列,它是窗序列產生函數的返回結果。此外還利用MATLAB自帶的濾波器設計和分析工具進行參數調整與優化。在本設計中,將要求的參數輸入MATLAB程序中,可以快速地設計出所需的FIR數字濾波器,再將相應的指標要求代入,最后利用的濾波器分析函數freqz來分析所設計出的FIR數字濾波器的幅頻特性和相頻特性,并用圖形顯示函數plot將它們顯示出來。所設計的FIR數字濾波器幅頻特性和相頻特性如圖1所示。

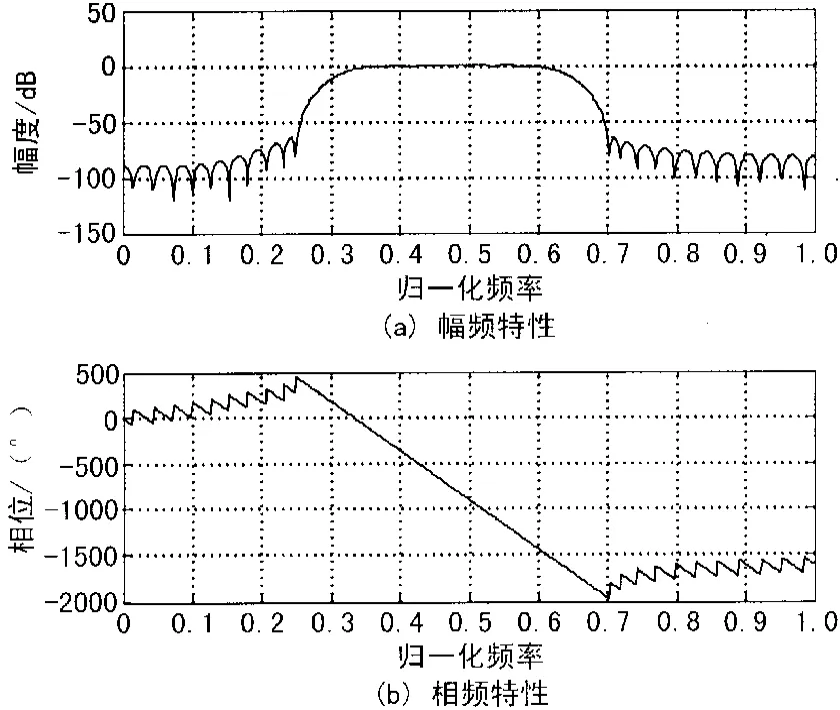
圖1 FIR數字濾波器特性圖

2 FIR數字濾波器的實現

DSP芯片是一種實時、快速、適于實現各種數字信號處理運算的微處理器。由于它具有豐富的硬件資源、高速的數據處理能力和強大的指令系統,因此在通信、航空、航天、雷達、工業控制及家用電器等領域得到廣泛應用。目前DSP芯片的運算分為定點和浮點2種,實際工程應用中常采用定點DSP芯片來實現所設計的FIR數字濾波器,并對其中幾個關鍵問題進行說明,在系統設計中具有重要的參考價值。

2.1 點數的確定

在定點DSP芯片中,采用定點數進行數值運算,其操作數一般采用整型數來表示。DSP芯片所給定的字長決定了整型數的最大表示范圍,一般為16位或24位。字長越長,所能表示的數的范圍越大,精度也越高。在濾波器的實現過程中,由于得到的數值可能是整數,也可能是小數或混合小數;DSP在執行算術運算指令時,并不確定所要處理的數據是整數還是小數,因此,在編程時必須指定一個數的小數點處于哪一位,這就是點數的確定。

在使用定點DSP芯片時,Q值的選擇是一個關鍵性問題,從DSP芯片運算的處理過程來看,實際參與運算的都是變量,而作為一個物理參量都有一定的動態范圍,只有確定動態范圍,才能確定Q值。因此,在程序設計前,首先要找出參與運算的所有變量的變化范圍,充分估計運算中可能出現的各種情況,然后再選擇采用何種確定點數來保證運算結果正確可靠。這里,通過理論分析法和統計分析法確定變量絕對值最大值|max|,然后根據|max|再確定Q值。

2.2 誤差問題

由于在使用定點DSP芯片實現FIR數字濾波器時,所有的數據都是定長的,運算也都是定點運算,因而會產生有限字長效應。所產生的誤差主要包括:數模轉換引起的量化誤差、系數量化引起的誤差以及運算過程中的舍入誤差。盡管在使用定點DSP芯片時,產生誤差是不能避免的,但是可以通過一些方法來減小誤差。例如可以用2個存儲單元來表示一個數,運算時使用雙字運算;可以根據需要將濾波器系數都用雙字表示,也可以只將一半的系數用雙字表示,視需要而定;另外,FIR數字濾波器和IIR數字濾波器所引入的量化誤差是不一樣的。FIR數字濾波器主要采用非遞歸結構,因而在有限精度的運算中是穩定的;而IIR數字濾波器是遞歸結構,極點必須在z平面單位圓內才能穩定,這種結構運算中的四舍五入處理有時會引起寄生振蕩。除了有限字長效應以外,不同結構引入的誤差也有所不同。在實際設計中,要注意實現中的誤差問題。在選擇不同的結構時,應考慮它們所引入的誤差,并用高級語言進行定點仿真,比較不同結構下誤差的大小,從而做出合理選擇。

2.3 循環尋址

DSP芯片中經常用到循環尋址的方法。該尋址方法可以對一塊特定存儲區實現循環的操作。把循環尋址理解為實現一個滑動窗,新數據引入后將覆蓋老的數據,便得該窗中包含了需處理的最新數據。在數字信號處理中的FIR、卷積等運算中,循環尋址具有極其重要的意義。

在TI公司的DSP芯片中,循環尋址通過如下方法實現:

①設定BK(寄存器塊大小)值,以確定循環尋址緩沖區的大小,也可將它看作是循環的周期;

②設定緩沖區的底部地址。必須注意:其低N位為零,其中N為滿足式2N＞BK的最小N值;

③用輔助寄存器間接尋址循環緩沖區。

在利用DSP芯片實現所設計的FIR數字濾波器過程中,應充分考慮以上3個具體步驟,以達到最佳實現結果。在具體的實現過程中,采用匯編語言進行編程,將通過MATLAB所設計得到的濾波器參數輸入,編譯后可生成可執行文件(.out),將可執行文件通過JTAG接口下載到TMS320VC5416DSP目標板,運行后即可實現所設計的FIR數字濾波器。

3 結束語

數字濾波器的應用十分廣泛,通過濾波器可以濾除輸入信號中不需要的成分,改善波形質量。FIR數字濾波器以它優越的性能,在數字信號處理領域占有很重要的地位。將MATLAB的功能與DSP芯片結合,運行MATLAB語言,可較容易地設計出具有嚴格要求的濾波器。采用DSP芯片實現的FIR濾波器,不僅具有準確度高、執行速度快等特點,而且程序可移植性好,實用性強,便于實現滿足更高采樣率的數字信號的實時濾波處理。

[1]趙順珍.馬 英.基于DSP的FIR數字濾波器設計與實現[J].微計算機信息,2009,25(2):29-31.

[2]張 萍.基于MATLAB與DSP的FIR數字濾波器的設計[J].中國科技信息,2007(23):80-81.

[3]徐金燕,李 明,鄭君麗.FIR濾波器的FPGA實現[J].無線電技術,2006(1):15-20.

[4]劉玉明,劉翠英,張寶華.一類FIR濾波器的加權最小方差設計[J].無線電工程,2000(4):52-54.