鋼筋混凝土組合梁的ANSYS有限元程序驗證

張旭宏，董艷秋

(黑龍江工程學院，哈爾濱 150050)

本文采用有限元分析方法對組合梁的工作性能，主要側重于使用階段的變形、極限狀態下的承載力、鋼梁與混凝土板間的滑移效應進行模擬分析。模型中假設在達到承載力極限狀態之前鋼梁不發生屈曲，并按小變形假設進行分析。材料的本構關系和滑移曲線等參數均根據相關實驗及理論公式得到，以反映混凝土開裂、鋼材屈服及栓釘變形等非線性特性。

目前，商業化的有限元軟件已經發展比較成熟，應用日趨廣泛。本文采用ANSYS8.0大型通用有限元軟件，對組合梁進行三維非線性分析。

1 有限元模型

混凝土采用8節點Solid65實體單元建模。該單元能夠模擬混凝土的拉裂和壓碎效應，還可以用加筋功能建立鋼筋混凝土模型。單元由8個節點定義，每個節點有三個自由度。鋼梁采用4節點的Shell43塑性大應變殼單元建模。該單元每個節點有平動和轉動共6個自由度，并具有塑性、應力剛化、大變形和大應變等功能。栓釘縱向抗剪作用由Combin14彈簧－阻尼單元或Combin39非線性彈簧單元模擬。Combin14單元為線性彈簧單元，通過定義彈簧剛度系數K來模擬栓釘變形。如果考慮栓釘非線性特性，模型中則使用Combin39非線性彈簧單元。縱向鋼筋采用Link8三維桿單元建模。該單元是桿軸方向拉壓單元，每個節點具有三個平動自由度。單元不承受彎矩和剪力作用，具有塑性、蠕變、膨脹、應力剛化、大變形和大應變等功能。當考慮鋼筋與混凝土之間滑移時，單元節點通過彈簧單元與混凝土節點相連接;當忽略滑移效應時，鋼筋與混凝土單元節點直接耦合。

現有文獻［1］表明，組合梁在外荷載作用下鋼梁和混凝土板之間會發生分離即掀起趨勢，同時在栓釘內會產生一定拉力，這一點與推出試驗中栓釘的受力狀態有所不同。但這種作用相對于縱向滑移等其它作用，對組合梁整體性能的影響較小，栓釘內的拉力也很小。同時考慮到有限元分析采用是小變形假定，因此建模時直接將混凝土板與鋼梁上翼緣相鄰節點橫向與豎向自由度耦合而忽略了掀起作用。

橫向鋼筋對組合梁的縱向抗剪能力能夠發揮很大作用，同時能顯著提高混凝土板橫向剛度和承載力。有限元模型采用Solid65單元中彌散鋼筋模擬橫向鋼筋，這種方法不能反映橫向鋼筋對組合梁縱向抗剪能力提高作用 (彌散型鋼筋沒有抗剪能力)，但可以提高混凝土板強度和剛度，當荷載直接作用于混凝土板時有利于保證計算的收斂性［2］。

2 鋼梁與混凝土板間滑移模型

已有研究成果提出了多種栓釘縱向剪力－滑移曲線。其中應用比較廣泛為Ollgaard于1971年提出的模型，公式形式如下:

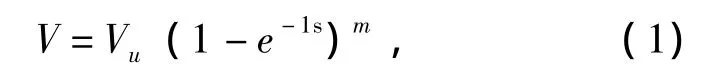
式中:Vu為栓釘的極限承載力，N;S為滑移，mm;m、n為不同學者提出的參數;公式提出栓釘荷載－滑移曲線如圖1所示。

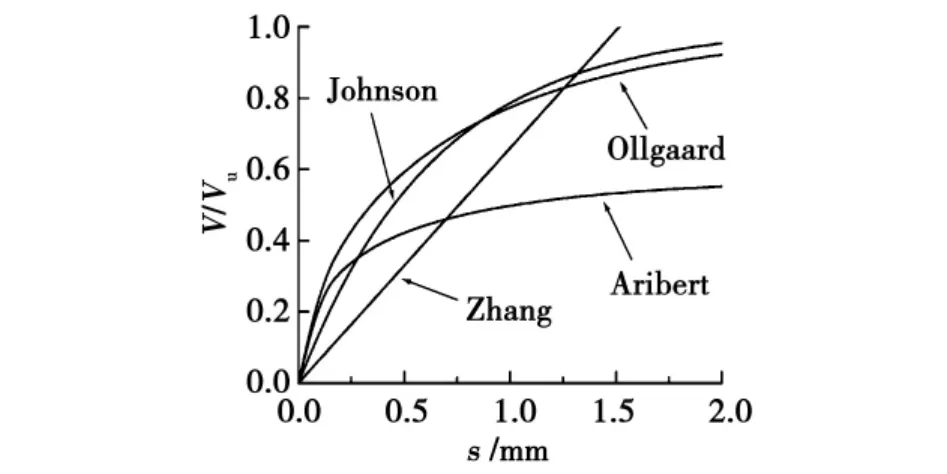
圖1 栓釘剛度曲線Fig.1 Stiffness curve of peg

在分析中采用模型栓釘布置情況如圖2所示，且在正、負彎矩作用下取用相同的滑移關系曲線。

圖2 鋼梁與混凝土板之間的剪切－滑移模型Fig.2 Shear－slip model between steel beam and concrete slab

對于栓釘極限滑移能力，一般可達栓釘直徑的30%，其計算式為:

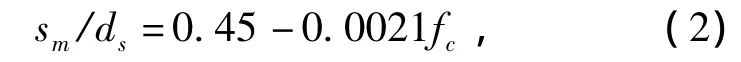
式中:sm為表示極限滑移值，mm;ds為表示栓釘直徑，mm。

一般情況下有限元分析得到滑移量均不超過此限值，因此在建模過程中未考慮栓釘破壞準則。

3 計算程序驗證

文獻［3－5］分別對正、負彎矩作用下的簡支組合梁進行了試驗研究。選擇其中兩組試件SCB23、SCB24和SB7、SB8進行ANSYS模擬分析。試件加載簡圖如圖3和圖4所示。

圖3 正彎矩作用下加載圖 (mm)Fig.3 Loading graph under positive bending moment(mm)

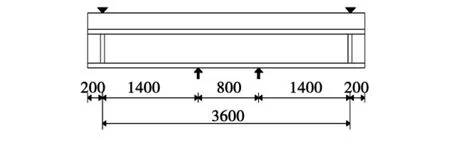
圖4 負彎矩作用下加載圖 (mm)Fig.4 Loading graph under negative bending moment(mm)

組合梁試件中的鋼梁均采用I20a軋制工字型鋼，材質為Q235;剪力連接件采用D16栓釘，沿梁軸線單排、均勻布置。試件的截面尺寸和材料參數見表1和表2。表中:bc、hc為混凝土板寬度和高度;fsy為鋼梁的屈服強度;fry為縱向鋼筋屈服強度;fcu為混凝土立方體 (150×150×150 mm3)強度;N和Nf分別表示剪跨內實際布置的栓釘個數和按照完全剪力連接設計時所需栓釘的個數，N/Nf表示剪力連接程度系數。

3.1 ANSYS分析

3 .1 .1 單元類型選取

對混凝土板模擬采用Solid65單元;對鋼梁模擬采用Shell43單元;對栓釘連接件模擬采用Combin39非線性彈簧單元;對縱向鋼筋模擬采用Link8單元。

3 .1 .2 幾何模型建立

I20a軋制工字型鋼的截面尺寸如圖5所示，組合梁的幾何模型如圖6所示。

3 .1 .3 有限元模型建立

不同組合梁試件中剪力連接件配置情況，在布置連接件單元時，模型網格在橫向劃分有所不同，在縱向保持一致。在鋼梁與混凝土板交界面上劃分了數目相同單元，所以交界面上節點具有一一對應關系，以方便連接單元布置。考慮到有限元分析采用是小變形假定，建模時直接將混凝土板與鋼梁上翼緣相鄰節點橫向與豎向自由度耦合而忽略了掀起作用。具體的網格劃分如圖7所示。

表1 文獻［3］中組合梁試件截面尺寸和材料參數Tab.1 Sectional dimensions and material parameters of composite beam specimen in literature［3］

表2 文獻［4］中組合梁試件截面尺寸和材料參數Tab.2 Sectional dimensions and material parameters of composite beam specimen in literature［4］

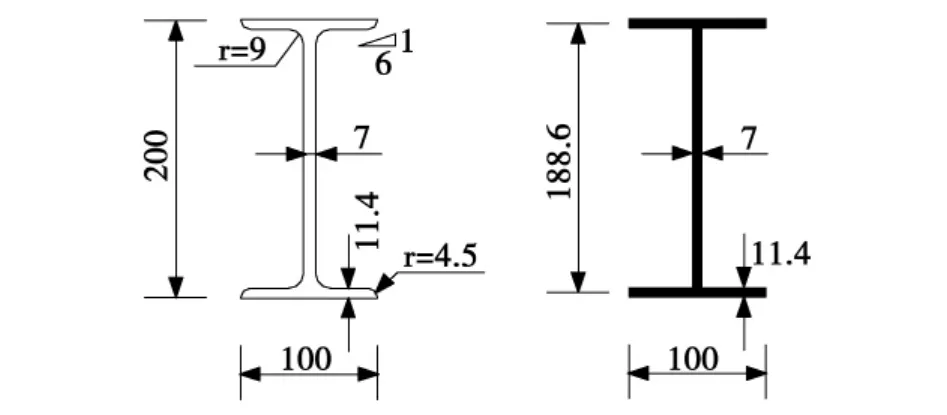
圖5 型鋼等效模型 (mm)Fig.5 Equivalent model of section(mm)

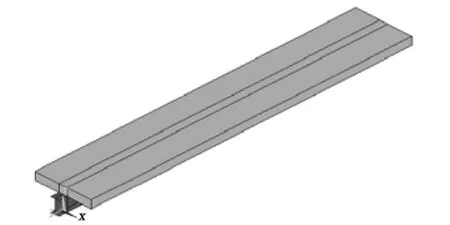
圖6 組合梁幾何模型Fig.6 Geometric model of composite beam

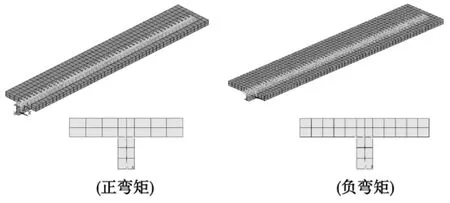
圖7 組合梁有限元模型Fig.7 Finite element model of composite beam

3 .1 .4 對支座添加約束

計算模型采用簡支，在梁的一端添加x、y、z三向位移約束，在梁的另一端添加y、z兩向位移約束。添加支座位移約束后計算模型如圖8所示。

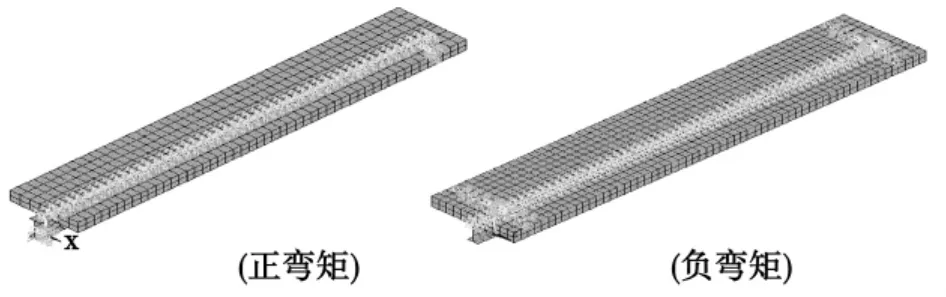
圖8 對組合梁支座添加位移約束Fig.8 Applied displacement constraint on support of composite beam

3 .1 .5 施加荷載

由于試驗中千斤頂通過分配梁在距梁端1 600 mm(正彎矩作用)或1 400 mm(負彎矩作用)處兩點加載，計算模型將試驗中所加的荷載換算為集中荷載施加在距梁端1 600 mm和1 400 mm節點上。施加節點集中荷載后的計算模型如圖9所示。

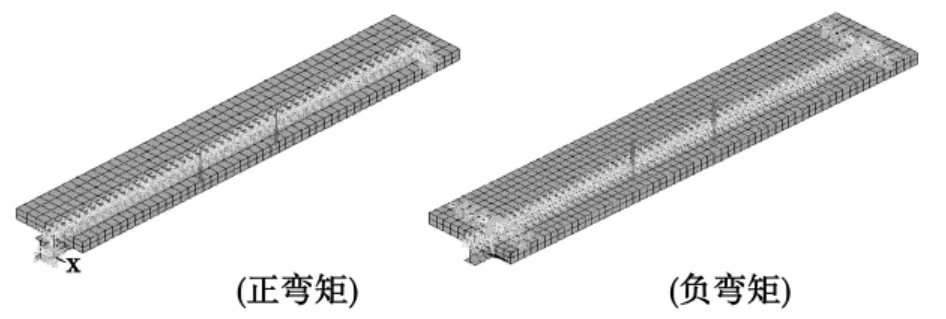
圖9 對組合梁施加荷載Fig.9 Applied load on composite beam

3 .1 .6 對支座局部加強

由于在加載過程中支座處局部應力特別大，在模擬計算過程中往往是支座處產生較大變形而使計算無法繼續進行。為了避免局部應力集中導致計算不收斂，在組合梁模型支座處建立了加勁肋單元［6，7］。

3.2 ANSYS計算結果

3 .2 .1 彈性階段

正、負彎矩作用情況分別以SCB23和SB7為例進行分析。組合梁試件在彈性階段的變形圖和應力圖分別如圖10、11和圖12、13所示。

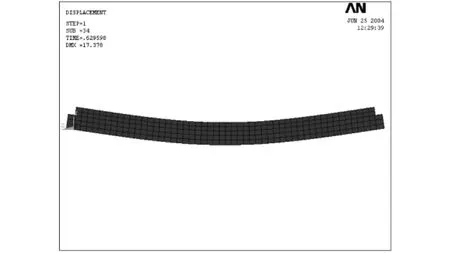
圖10 SCB23在彈性階段變形圖Fig.10 Deformation graph of SCB23 within elastic stage

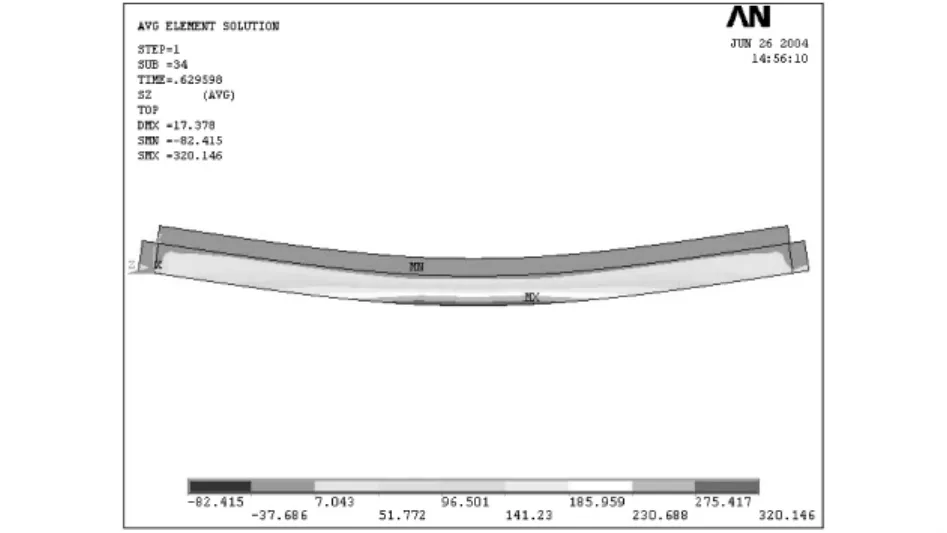
圖11 SCB23在彈性階段應力圖Fig.11 Stress graph of SCB23 within elastic stage

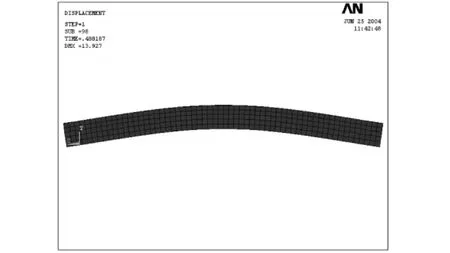
圖12 SB7在彈性階段變形圖Fig.12 Deformation graph of SB7 within elastic stage

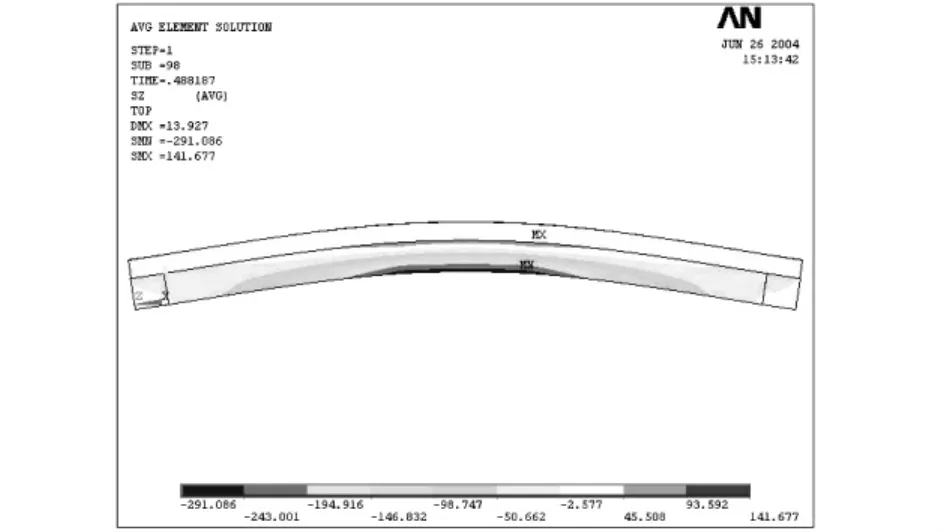
圖13 SB7在彈性階段應力圖Fig.13 Stress graph of SB7 within elastic stage

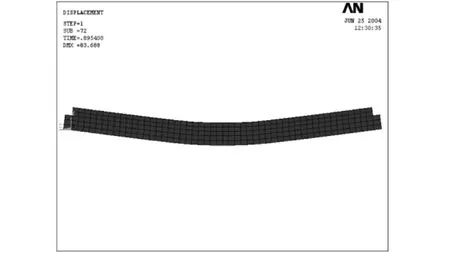
圖14 SCB23彈塑性階段變形圖Fig.14 Deformation graph of SCB23 within elastic plastic stage

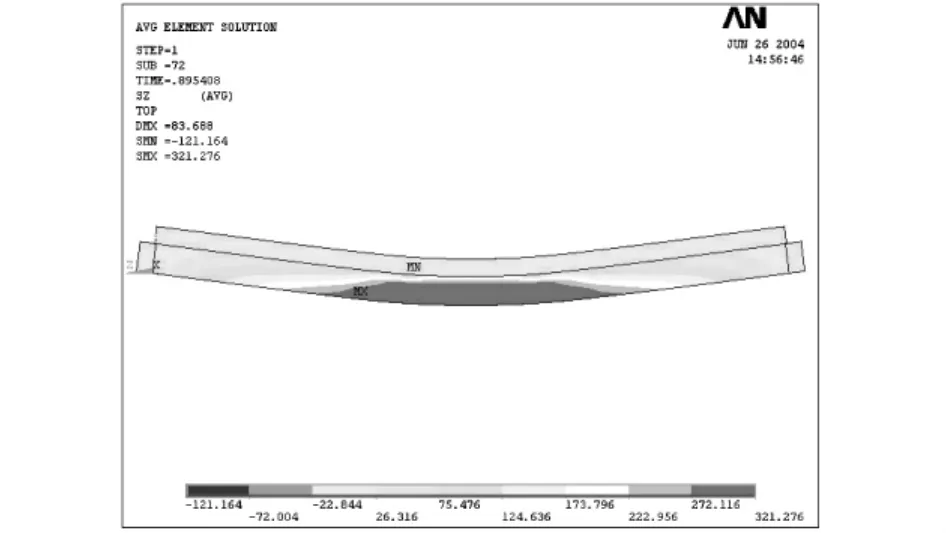
圖15 SCB23彈塑性階段應力圖Fig.15 Stress graph of SCB23 within elastic-plastic stage

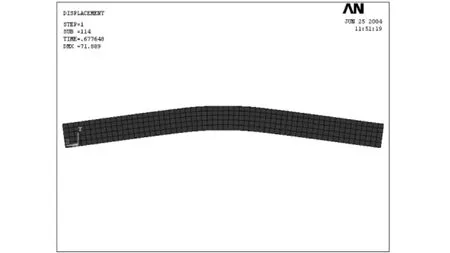
圖16 SB7彈塑性階段變形圖Fig.16 Deformation graph of SB7 within elastic-plastic stage

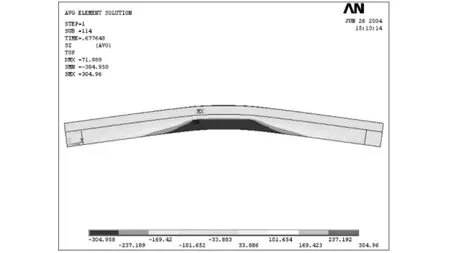
圖17 SB7彈塑性階段應力圖Fig.17 Stress graph of SB7 within elastic-plastic stage

由變形圖可知，在彈性極限狀態，試件SCB23跨中截面最大撓度為17.378 mm，相應跨中彎矩為141 kN·m;試件SB7跨中截面最大撓度為13.927 mm，相應跨中彎矩為95.7 kN·m。由應力圖可以觀察到，此時試件SCB23的鋼梁下翼緣剛好進入受拉屈服階段，而試件SB7鋼梁下翼緣也剛好進入受壓屈服階段［8］。

圖18 彈塑性階段混凝土板應力圖Fig.18 Stress graph of concrete floor within elastic-plastic stage

3 .2 .2 彈塑性階段

試件SCB23、SB7在彈塑性階段的變形圖和應力圖分別如圖14、15和圖16、17所示，混凝土板應力分布情況如圖18所示。

由變形圖可以觀察到，在承載力極限狀態，試件SCB23跨中截面最大撓度為83.688 mm，相應跨中彎矩為200.6 kN·m;試件SB7跨中截面最大撓度為71.889 mm，相應跨中彎矩為131.3 kN·m。由應力圖可以觀察到，此時無論是在正彎矩還是負彎矩作用下，組合梁中鋼梁下翼緣往上屈服區均發展的比較充分，幾乎全截面達到屈服［9］。由圖18可知，混凝土板也達到了抗壓強度而被壓碎。

3 .2 .3 ANSYS計算結果與試驗結果對比分析

ANSYS計算結果與試測數據的對比情況見表3。其中，My和Mye分別為鋼梁下翼緣開始屈服時跨中彎矩實測值和有限元計算值;Mu和Mue分別為極限彎矩實測值和有限元計算值;fy和fu分別為對應于My和Mu實測跨中撓度;fye和fue分別為對應于Mye和Mue有限元計算跨中撓度;N/Nf為組合梁試件的剪力連接程度系數。

由對比結果可知，除剪力連接程度較低的組合梁試件SCB24的極限撓度外其余有限元計算結果均與實測數據吻合良好，計算誤差都在10%內。由于本文側重于組合梁使用階段變形研究，所以極限撓度計算誤差不會為以后分析帶來較大影響。因此，從整體上看，有限元結果與試驗結果符合良好，說明使用ANSYS程序對組合梁進行非線性有限元分析方法是行之有效的。見表3。

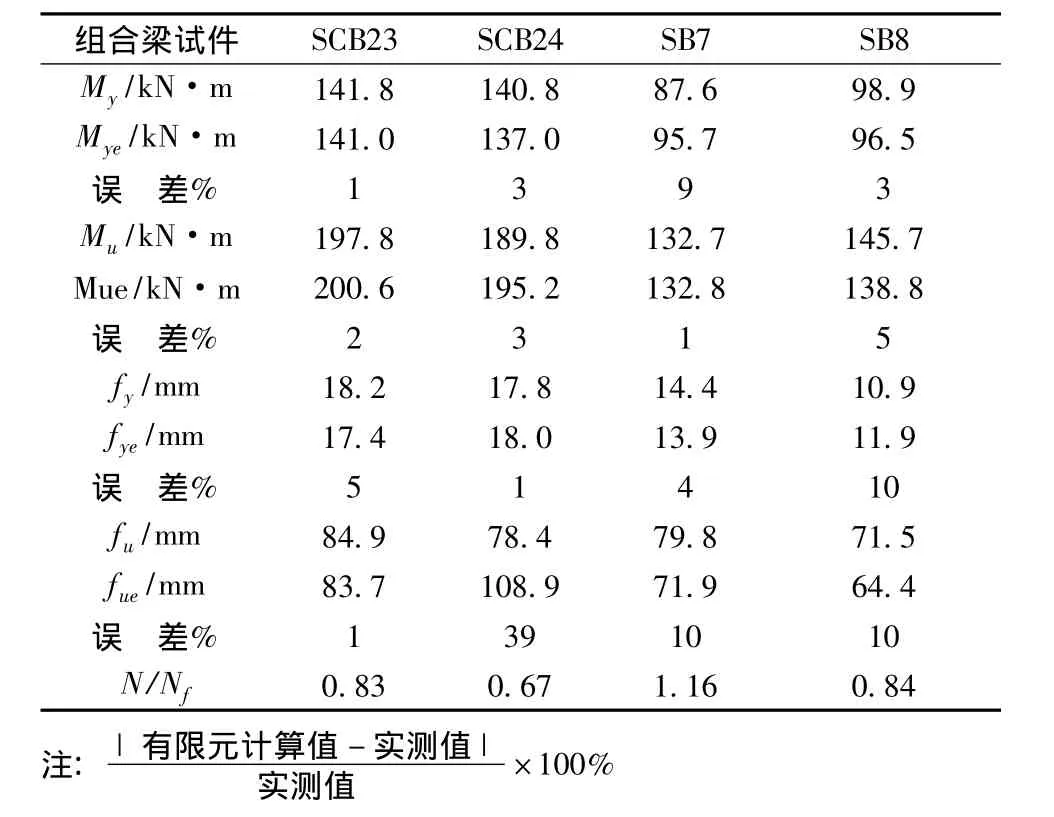
表3 有限元結果與試驗結果對比Tab.3 Comparation of FEM result and test result

4 結束語

主要針對有限元分析中所使用到的單元類型、材料屬性及非線性方程組求解方法進行了基本介紹。所選用有限元模型能夠較好地反映混凝土和鋼材非線性性質以及混凝土板與鋼梁之間滑移性能。算例分析結果表明，使用ANSYS程序對組合梁進行有限元分析方法是可行的。

［1］朱聘如.鋼－混凝土組合梁設計原理［M］.北京:中國建筑工業出版社，1989.

［2］王連廣，李立新，劉之洋.鋼桁架與混凝土組合梁滑移與掀起的空間計算分析［J］.東北大學學報 (自然科學版)，2000(4):439－442.

［3］聶建國，沈聚敏，袁彥聲，等.鋼－混凝土組合梁中剪力連接件實際承載力的研究［J］.建筑結構學報，1996(2):21－28.

［4］樊健生.鋼－混凝土連續組合梁的試驗及理論研究 ［D］.北京:清華大學，2003.

［5］孫 航，盛洪飛，程 偉，等.大跨度剛構——連續組合梁橋施工控制技術研究［J］.森林工程，2006，22(5):39－41.

［6］鄭則群，房貞政.剪力連接件對預應力鋼－混凝土組合梁受力性能的影響［J］.福州大學學報 (自然科學版)，2001(1):74－77.

［7］陳世鳴，顧 萍.影響鋼－混凝土組合梁撓度計算的幾個因素 ［J］.建筑結構，2004(1):31－33.

［8］周 奇，張 南，洪英維.體外預應力鋼箱——混凝土組合梁的預應力損失的計算方法［J］.公路工程，2007(4):40－44.

［9］周 奇，張 南，許 琦.預應力鋼混凝土組合梁預壓應力分布研究 ［J］.公路工程，2008(1):28－31.