軸壓鋼管混凝土柱的有限元分析

湯杰瑤 吳超華

0 引言

鋼管混凝土結(jié)構(gòu)具有抗壓承載力高、塑性和韌性好、耐火性能較好等一系列的優(yōu)點,可提供極好的抗震性能。另外,在施工階段省去了支模和拆模的工序,因而施工方便,施工周期短,經(jīng)濟效益好,具有廣闊的發(fā)展前景。在近幾十年來鋼管混凝土發(fā)展迅速,在工業(yè)廠房、橋梁結(jié)構(gòu)、地下結(jié)構(gòu)、高層和超高層建筑中取得了良好的經(jīng)濟效益和建筑效果。

鋼管混凝土同時具備了鋼管和混凝土兩種材料的性質(zhì),并利用鋼管和混凝土兩種材料在受力過程中的相互作用,增強了整個鋼管混凝土柱的延性和承載力[1]。此外,鋼管混凝土的極限承載受多方面因素的影響,如混凝土受到的約束力以及鋼管的幾何屬性等。

本文以鋼管混凝土柱為研究對象,簡單概述了鋼管混凝土軸壓性能理論方法,并采用非線性有限元程序ABAQUS,對4根軸心受壓下的鋼管混凝土柱進行有限元分析,得到了各柱的荷載—應變?nèi)^程曲線,與相關的試驗數(shù)據(jù)進行對比,以驗證所建立有限元模型的正確性。

1 鋼管混凝土軸壓短柱受力性能理論分析方法

鋼管混凝土軸壓短柱受力性能理論分析可分為極限分析和全過程分析。

在極限分析中,代表性的理論有極限平衡理論,即不管加載歷史和變形過程,直接根據(jù)結(jié)構(gòu)處于極限狀態(tài)時的平衡條件計算出極限狀態(tài)的最大荷載值。蘇聯(lián)學者格沃茲杰夫教授是第一個用極限平衡法求解鋼管混凝土軸心受壓短柱極限承載能力的學者,我國的蔡紹懷[1]、湯關祚[2]等人也做了大量研究工作。

全過程分析法,采用的理論分析方法可分為縱向纖維模型法、合成法和有限元法。縱向纖維模型法[2],即給定鋼材和核心混凝土的軸向應力—應變關系式來代替真實的鋼管混凝土三向受力狀態(tài),直接按相同縱向應變的應力疊加得到鋼管混凝土軸壓短柱的荷載—應變?nèi)€,回避了鋼管混凝土之間的作用機理。

合成法(韓林海[3]、鐘善桐[4]),即通過對鋼管混凝土軸壓短柱的試驗數(shù)據(jù)分析,由鋼材的本構(gòu)模型扣除其承載力,剩余即為核心混凝土的承載力,通過大量試驗結(jié)果的運算,由此擬合得到核心混凝土的本構(gòu)關系;然后利用鋼材的彈塑性本構(gòu)模型和混凝土的非線性彈性本構(gòu)模型,按內(nèi)外力平衡條件和變形協(xié)調(diào)條件迭代求解。但合成法也無法合理解釋加載過程中鋼管和核心混凝土受力變化情況,不易揭示鋼管混凝土受力機理,在效果上與縱向纖維模型法一致。

有限元法,鋼材采用實體元或殼單元,Von-Mises彈塑性本構(gòu)模型,混凝土一般都采用三維實體元,對混凝土本構(gòu)模型編寫程序或采用大型有限元非線性程序中確定的混凝土本構(gòu)模型。有限元模型力學概念清晰,求解精度較高,并隨著計算機科學的發(fā)展,愈來愈顯示出強大的生命力。但三維實體有限元分析往往具有龐大的自由度,需要進行大量的數(shù)值計算。

2 材料本構(gòu)關系

對于全過程分析法,需要給定鋼材和混凝土的本構(gòu)模型,鋼管混凝土數(shù)值分析的關鍵在于核心混凝土本構(gòu)模型的確定,而尋求一種既能較全面反映混凝土各種特性,又能便于實際計算的本構(gòu)關系模型尚要進一步研究[6]。目前,在鋼管混凝土受力分析中得到應用的混凝土本構(gòu)模型有以彈性力學為基礎的非線性彈性本構(gòu)模型、塑性—斷裂理論和內(nèi)時理論以及各大型有限元商業(yè)軟件中給定的混凝土本構(gòu)模型等。其中Mander[7]等對約束混凝土進行了深入的研究,應用William-Warnke五參數(shù)強度準則計算約束混凝土軸向極限強度,并采用Popovics應力—應變表達式建立了約束混凝土的本構(gòu)關系。該模型能較好地反映隨約束效應的提高約束混凝土的極限強度及峰值應變相應增大、下降段趨于平緩等現(xiàn)象。

3 軸心受壓下鋼管混凝土的數(shù)值分析

ABAQUS是基于有限元方法的工程模擬軟件,該軟件功能強大,具備豐富的單元庫和材料模型庫,可以模擬大多數(shù)典型工程材料的性能。本節(jié)使用非線性有限元程序ABAQUS對4根軸心受壓下的鋼管混凝土試件柱進行有限元分析,得到荷載—應變?nèi)^程曲線和極限承載力,并將分析結(jié)果與相關的試驗數(shù)據(jù)進行對比,以驗證有限元模型的正確性。

3.1 試驗數(shù)據(jù)

表1列出了4根圓鋼管混凝土柱的幾何和材料屬性,其中,D為鋼管直徑;t為鋼管厚度;D/t為徑厚比;L為鋼管柱長度;fy為鋼管的屈服強度;fc′為核心混凝土的強度。圖1為試驗得到的鋼管混凝土柱在軸心受壓狀態(tài)下的荷載—應變曲線。

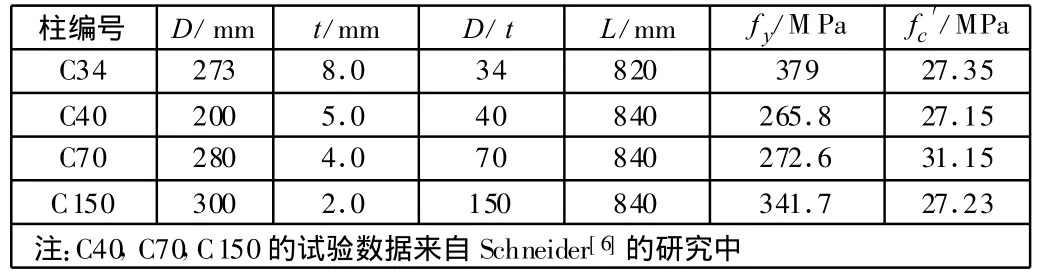
表1 圓鋼管混凝土的幾何和材料屬性

3.2 有限元建模

在有限元網(wǎng)格中,鋼管與核心混凝土采用27—節(jié)點實體單元模擬,每個節(jié)點有3個自由度。鋼管本構(gòu)采用von Mises屈服準則、相關流動法則以及各項同性應變強化的彈塑性模型;核心混凝土采用Mander模型,用Drucker-Prager屈服準則模擬混凝土的屈服面,并基于相關流動法則和各向同性硬化準則模擬混凝土的響應。為了模擬鋼管與核心混凝土的粘結(jié)作用,法向上采用基于表面相互作用的接觸壓力—超閉合模型,切向上采用庫侖摩擦模型。

3.3 有限元分析與試驗對比

對4根鋼管混凝土柱的有限元分析結(jié)果與試驗值的對比見表2,各柱的軸心荷載—應變曲線以及相關的試驗曲線見圖2。荷載—應變曲線表明了鋼管混凝土在受荷過程中,核心混凝土由于受到鋼管的約束,其極限承載力有較大的提高,延性也得到顯著改善。總體來說,有限元分析結(jié)果與試驗數(shù)據(jù)吻合得相當好,誤差在可接受的范圍內(nèi),從而證明了有限元模型的正確性。

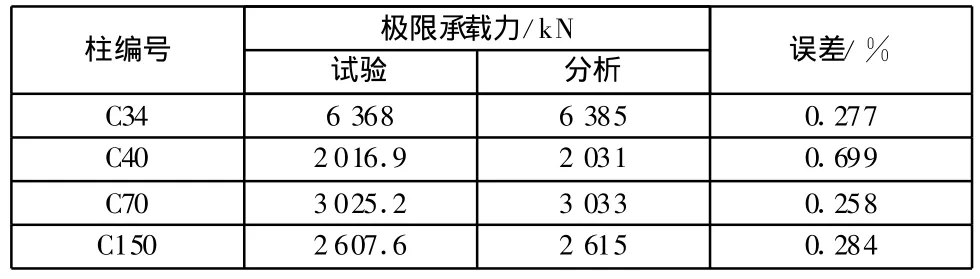
表2 分析結(jié)果與試驗值的對比

4 結(jié)語

本文簡單概述了鋼管混凝土軸壓性能的理論分析方法及本構(gòu)關系,以非線性有限元程序ABAQUS為平臺,選擇了合適的材料本構(gòu)模型和參數(shù),對4根軸心受壓下的鋼管混凝土柱進行有限元建模和分析,并得到了各柱的荷載—應變?nèi)^程曲線和極限承載力,最后將分析結(jié)果與相關的實驗數(shù)據(jù)進行對比,結(jié)果表明,有限元分析結(jié)果與試驗數(shù)據(jù)吻合得相當好,誤差在可接受的范圍內(nèi),驗證了有限元模型的正確性。

[1]蔡紹懷.現(xiàn)代鋼管混凝土結(jié)構(gòu)[M].北京:人民交通出版社,2003.

[2]湯關祚,招炳泉.鋼管混凝土短柱的基本力學性能的研究[J].建筑結(jié)構(gòu)學報,1982,3(1):12-31.

[3]韓林海.鋼管混凝土結(jié)構(gòu)[M].北京:科學出版社,2000.

[4]鐘善桐.鋼管混凝土結(jié)構(gòu)[M].第3版.北京:清華大學出版社,2003.

[5]韓林海.混凝土的本構(gòu)關系模型及其在鋼管混凝土數(shù)值分析中的應用[J].哈爾濱工業(yè)大學學報,1995,28(5):26-31.

[6]Mander.J.B,Priestley,M.J.N,et al.Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering,2006,114(8):1804-1826.

[7]Schneider,S.P.Axially loaded concrete-filled steel tubes[J].Journal of Structural Engineering,1998,124(10):1125-1138.