電動助力轉向系統的滑模變結構控制
徐冠林,石沛林,唐紹豐,唐俊杰
(山東理工大學交通與車輛工程學院,山東淄博255049)
電動助力轉向系統(electric power steering system,簡稱EPS)的控制方法多采用傳統的PID控制,該方法在系統參數特定的情況下可以基本滿足控制要求,但動態性能不理想.同時由于EPS系統參數變化、路面干擾等原因具有不確定性[1],使得PID控制的控制系數不能時刻處于最佳值.特定狀態下的最佳值,隨著系統參數變化,控制效果會變差.
滑模變結構控制方法的滑動模態對系統參數的攝動具有完全自適應性[2-4],可為具有不確定性因素的系統實現魯棒控制提供有效的控制方法.
1 EPS的數學模型
將EPS的結構進行合理簡化,并將系統中的阻尼等非線性部分忽略,對組成電動助力轉向系統的轉向管柱、助力電機和齒條分別進行受力分析.EPS簡化模型如圖1所示.
對轉向柱進行動力學分析,可得
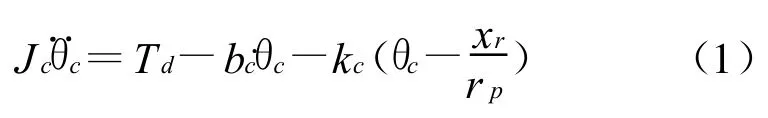
式中:Jc為方向盤、轉向管柱的等效轉動慣量;Td為方向盤輸入轉矩;bc為轉向管柱阻尼系數;kc為轉矩傳感器扭桿剛度;θc為方向盤轉角;xr為齒條位移;rp為小齒輪半徑.
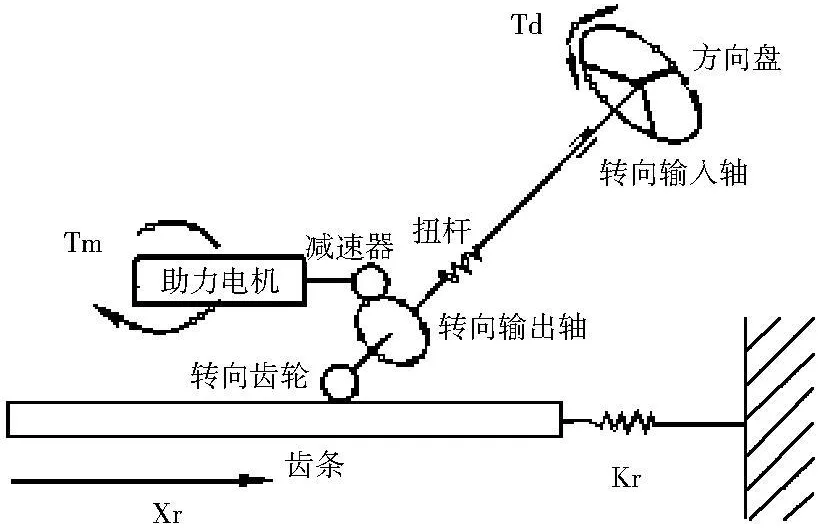
圖1 電動助力轉向系統簡化模型

齒條部分的數學模型:
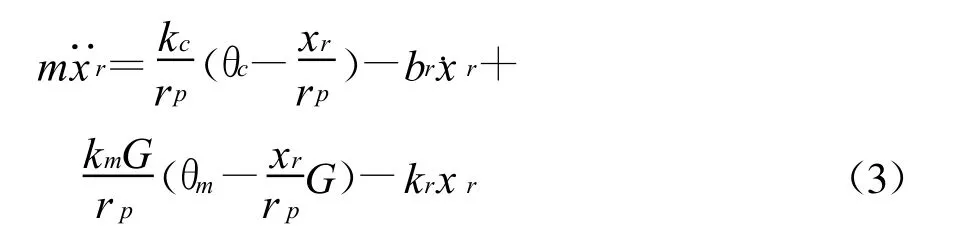
式中:m為齒條質量;rp為小齒輪半徑;br為齒條阻尼系數為電機軸剛度;G為減速器減速比為電機轉角為等效彈簧剛度.
EPS系統采用直流電機,電機電壓u與電感L、電樞電阻R、反電動勢系數、電機電流i的關系為

對電機機械部分進行動力學分析,可得
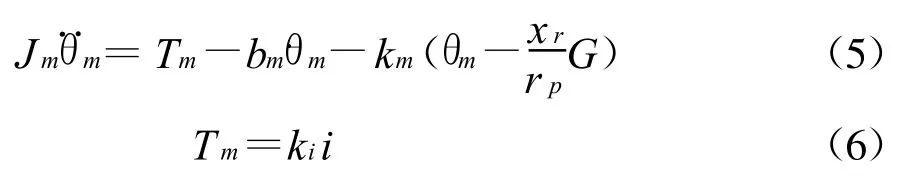
取狀態變量x1=θc,x2=˙θc,x3=xr,x4=˙xr,x5=θm,x6=˙θm,x7=i,由式(1)~(6)得到系統的狀態方程:

式中:
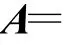

2 滑模變結構控制
滑模變結構控制本質上是一類特殊的非線性控制,其非線性表現為控制的不連續性,這是與其他控制的根本區別.滑模變結構控制使系統的“結構”隨時間的變化而變化,該特性可以迫使系統在一定特性下沿規定的狀態軌跡做小幅度、高頻率的上下運動,即“滑模”運動.這種滑動模態是可以設計的,并且與系統的參數和擾動無關,因此,處于滑模運動的系統具有良好的魯棒性.
為實現對目標電流的跟蹤,取切換函數s為電流誤差e,即
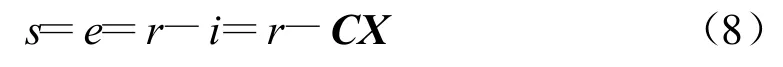
其中r為目標電流.
采用指數趨近律的控制方式,其趨近律slaw[5]為
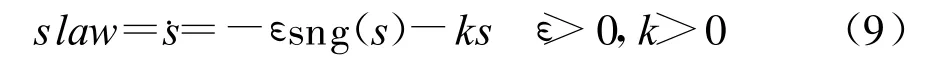
對式(8)求導,得
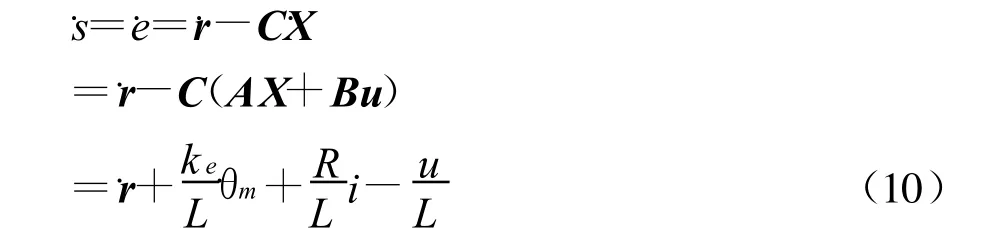
由式(10),可推導出控制器輸出量
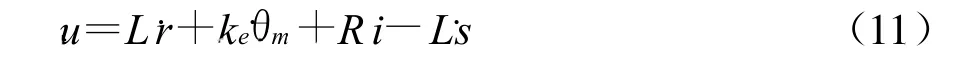
3 仿真計算與結果分析
在Matlab7.0下進行仿真計算,取目標電流為階躍信號:r=20 A,趨近律中的k=30,ε=5,對比不同控制方法的階躍響應.采用PID控制方法的助力電流階躍響應如圖2所示,可以看出助力電流有8%左右超調量而且調節時間約為0.18 s,采用PID控制方法可以基本滿足跟蹤目標電流的要求,但還不是很理想.由圖2可知,采用滑模變結構控制時的助力電流階躍響應沒有超調量而且調節時間短、穩態響應好,優于傳統的PID控制方法.
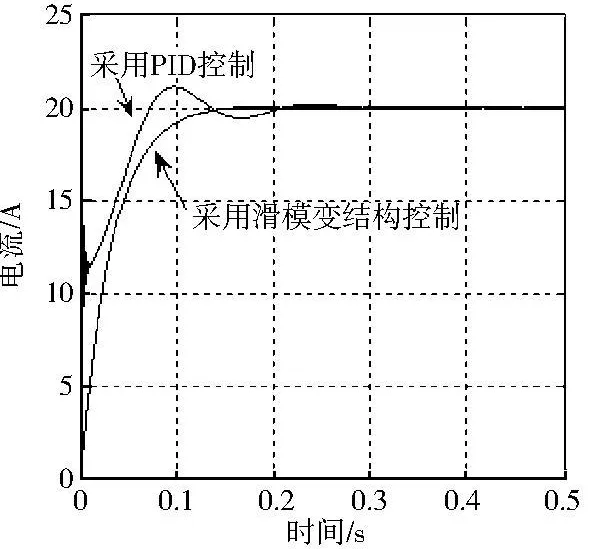
圖2 采用不同控制方法時助力電流階躍響應
實際上,仿真時采用的電機電樞的電阻值是整個電機回路的平均等效電阻值,對于旋轉的電機而言,不存在一個準確的電機電樞的電阻值[6].電機的電樞電阻R增大10%和20%時的傳統PID控制方法的助力電流階躍響應與原系統的比較,如圖3所示,當電樞電阻R增大10%時,超調量約為12%,當R增大20%時,超調量約為15%,并且調節時間也有所延長,可見對特定狀態下的系統,采用傳統的PID控制方法可以滿足系統需求,但是當系統的某一參數變化時,PID控制方法就不能達到滿意的控制效果.當電樞電阻增大10%和20%時,采用滑模變結構控制方法的助力電流階躍響應與原系統的階躍響應完全一樣;當電樞電阻增大60%時,采用滑模變結構控制方法的助力電流階躍響應才發生微小變化,只是在0.13 s時稍稍偏離逼近目標電流軌跡,然后迅速又升高至目標電流,如圖3所示.由此可見,滑模變結構控制的滑動模態對系統參數的攝動具有完全的自適應性,可以為這類不確定性系統實現魯棒控制提供有效方法.
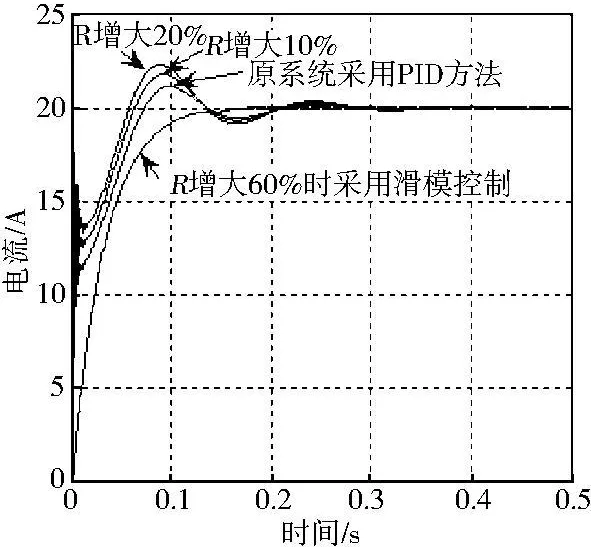
圖3 參數變化時兩種控制方法的階躍響應
4 結束語
通過對EPS建立數學模型,采用指數趨近律方法設計了滑模變結構控制器,并進行了仿真.仿真結果表明與傳統的PID控制方法相比,滑模變結構控制器沒有超調量、調節時間較短,并且當系統參數發生變化時,助力電流階躍響應基本不變,可以對電動助力轉向系統進行魯棒控制.
[1] 石沛林,高士香,劉昭度,等.基于BP網絡的EPS系統仿真與PID整定研究[J] .微計算機信息,2009,25(13):92-94.
[2] 王豐堯.滑模變結構控制[M] .北京:機械工業出版社,1995.
[3] 王亮,任傳波,趙真,等.車輛主動懸架的模型跟蹤變結構控制研究[J] .山東理工大學學報(自然科學版),2009,23(2):20-23.
[4] Shyu Kuo-kai,Lin Ching-yao.Adaptive sliding mode control for variable structure systems with constraint control input[J] .Dynamics and Control,1996,6(1):49-61.
[5] 張翔,王德石.滑模控制器趨近律仿真研究[J] .微處理機,2008(1):17-18.
[6] 苗立東,何仁.電動助力轉向器電動機等效電阻測量方法[J] .實驗技術與管理,2006,23(03):35-37.

