含切口的混凝土試件承載力計算
何 敏,王利民,2,任 鵬
(1.山東理工大學交通與車輛工程學院,山東淄博255049;2.青島理工大學理學院,山東青島266033)
工程中經常用到的混凝土、巖石等準脆性材料內部往往存在空隙和缺陷,其結構損傷與破壞過程一般起始于應力集中部位,當應力與變形超過一定數值時,這些原有裂紋或缺陷會擴展、串接形成損傷帶,并最終導致構件的斷裂失效[1].文獻[2] 采用光彈性貼片法對6種大尺寸緊湊拉伸試件預制裂縫的起裂、穩定擴展直至失穩破壞的全過程進行了系統的研究,并用錄像機拍攝了光彈性貼片所顯示的裂紋擴展的全過程,得到了混凝土裂縫在不同載荷階段的完整而直觀的觀察結果.對于此類緊湊拉伸試件,文獻[3] 提出了考慮裂紋發展區增韌作用、以起裂強度因子和失穩強度因子為指標的雙K斷裂模型.文獻[4] 則分析了混凝土的承載能力、抗裂性能與齡期之間的關系.文獻[5] 對6種不同尺寸的混凝土緊湊拉伸試件做了實驗,計算了各試件的斷裂能并著重分析了它們的裂紋口張開位移、裂紋擴展長度和載荷三者之間的關系.文獻[6] 分析了緊湊拉伸試件中斷裂過程區的應力再分配和斷裂過程區域的大小同試件本身尺寸的關系即尺寸效應.
一般工程用混凝土結構尺寸都比較大,尤其是重要建筑物如高混凝土壩、核電站反應堆混凝土安全殼等,如能探求出估算大尺寸混凝土構件的最大承載力的方法,則對于估計這些重要建筑物的最大承載力將有一定的意義.本文在上述研究工作的基礎上,利用文獻[2] 中6種尺寸的大型混凝土緊湊拉伸試件的實驗結果,結合雙K準則與黏聚裂紋模型進行應力強度因子和承載力分析,以探討帶有預制裂紋的大尺寸混凝土構件的最大承載力的計算方法,進一步簡化實用設計公式.
1 混凝土緊湊拉伸斷裂實驗尺寸與數據分析
圖1中,設a為外力加載點到裂紋底尖點的距離,a0為a的初始值,即外力加載點到預制裂紋底部的距離,b為加載點到試件韌帶邊沿的距離,h、L、t分別為試件的總高度、寬度、厚度.各試件尺寸及最大載荷實驗值見表1.由表1中數據可以看出,試件尺寸越大,其承載力越大.
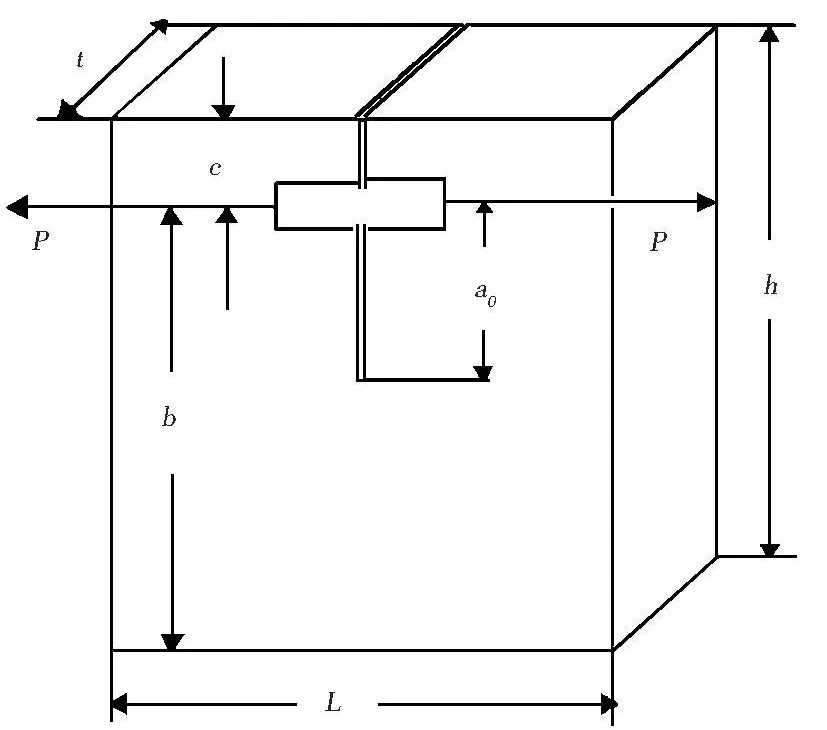
圖1 實驗試件幾何尺寸和加載方式
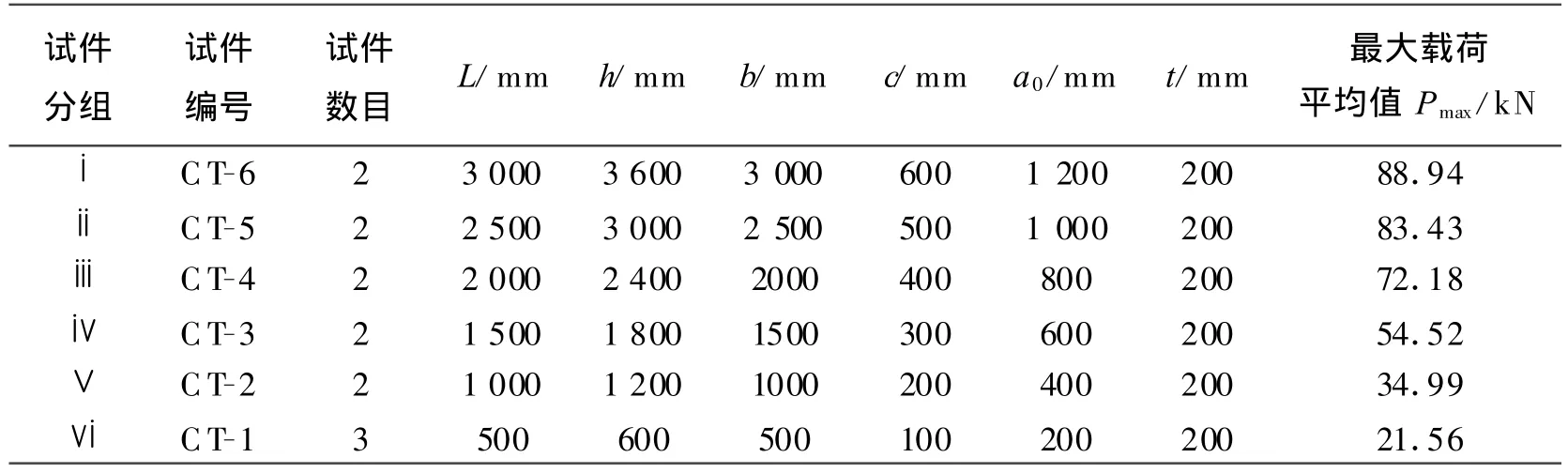
表1 試件的尺寸及實驗載荷最大值
2 應力強度因子計算
斷裂力學是分析含裂紋固體力學行為的學科,按照裂紋端部應力的不同分布形式,斷裂過程一般可分為三大類構型,即張開(Ⅰ)型,滑開(Ⅱ)型和撕開(Ⅲ)型[7].應力強度因子是表征材料中靠近裂紋尖端處在載荷作用下應力場奇異性的強度指標.線彈性應力強度因子與構件的幾何形狀及外載荷的大小有關,且與外載荷呈線性關系[8].對于帶預制裂紋的緊湊拉伸構件,其應力強度因子由文獻[3,9] 知,在a/b=0.2~0.8時,按公式
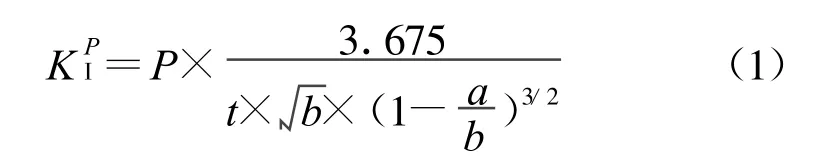
計算的應力強度因子與精確值的誤差不超過3.8%.
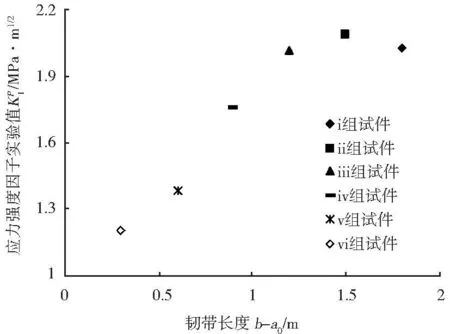
圖2 不同尺寸試件的應力強度因子
3 斷裂試件承載力估計值與實驗峰值平均值的對比
在加載實驗過程中,斷裂過程區與未受損區的分界點是非線性裂紋尖點,而預制裂紋尖端即割痕切口的根部是斷裂過程區的起點,設兩者之間的距離為裂紋擴展長度d.參照圖1,則d、a、a0及b的關系為
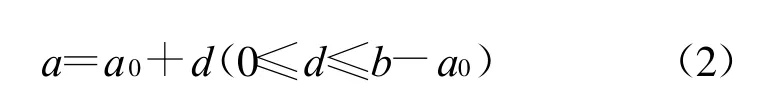
在裂紋擴展過程中,裂紋端部損傷區存在阻止裂紋擴展的相互作用力,該分布力會大大降低應力的奇異性,使得不同韌帶長度的結構承載力發生變化.參照文獻[2-3] 中分析準脆性材料的雙K斷裂準則,有


其中η為具有應力量綱的參數,它與材料的極限拉伸應力有關.從圖2中應力強度因子的尺寸效應看出,其變化趨勢符合式(4)中的應力強度因子與裂紋擴展長度的二分之一次冪成正比關系.將式(4)代入式(3),再將所得式與式(2)一并代入式(1)可得到載荷的計算式為
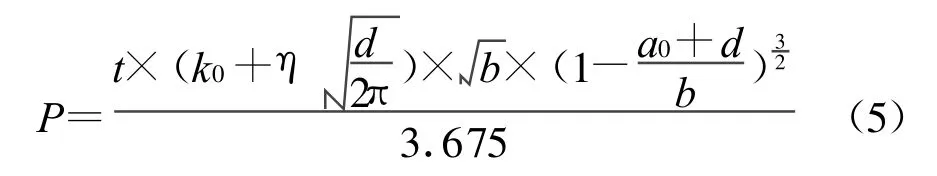
通過式(5)能夠計算繪制載荷P與裂紋擴展長度d的關系曲線,曲線的最高點為構件的最大承載力計算值.參見圖2中數據,由最大實驗載荷和預制裂紋尺寸得到的應力強度因子的數值在1~2.2 MPa?m1/2之間;又由式(3)可知,作為起裂應力強度因子的K0應小于其最小值,在此前提和在使各組試件的實驗峰值平均值的總和與對應的計算值峰值的總和基本相等的前提下,經過對K0和η取不同數值時的多次計算、擬合及驗證,發現在取材料參數K0=0.283MPa?m1/2,η=5.535 MPa時各組試件的計算峰值與實驗峰值平均值總體擬合效果最佳,其承載力與裂紋擴展長度關系如圖3所示.
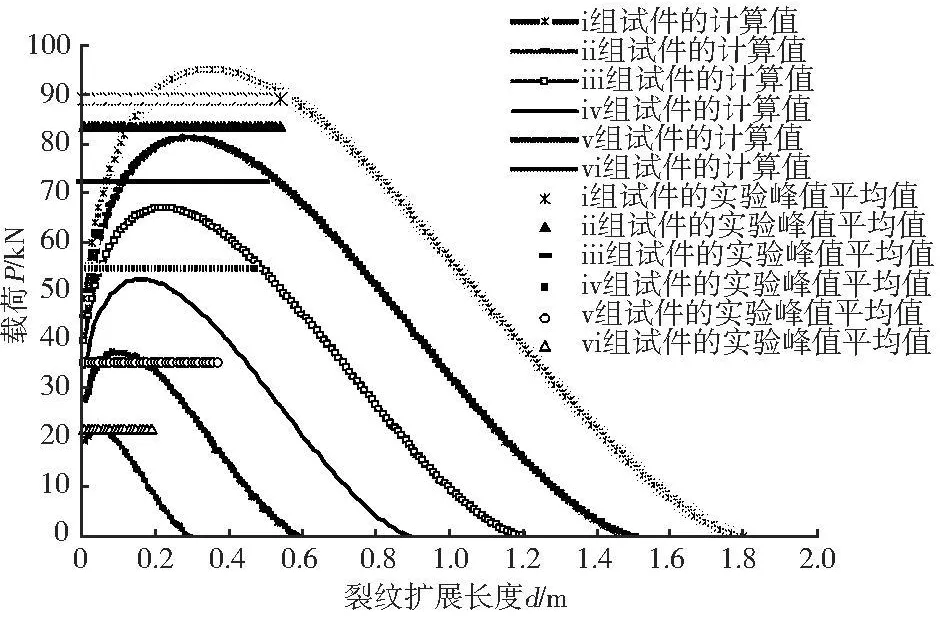
圖3 試件承載力P隨裂紋擴展長度d的變化曲線及與實驗峰值平均值的對比
現將各組試件所受載荷的實驗最大值平均值和用式(5)得到的理論計算值峰值及后者相對于前者的相對誤差列入表2中.由表2中數據可知,6個相對誤差中最大值為8.88%,說明用此方法計算此種構件失效時的最大承載力是可行的.
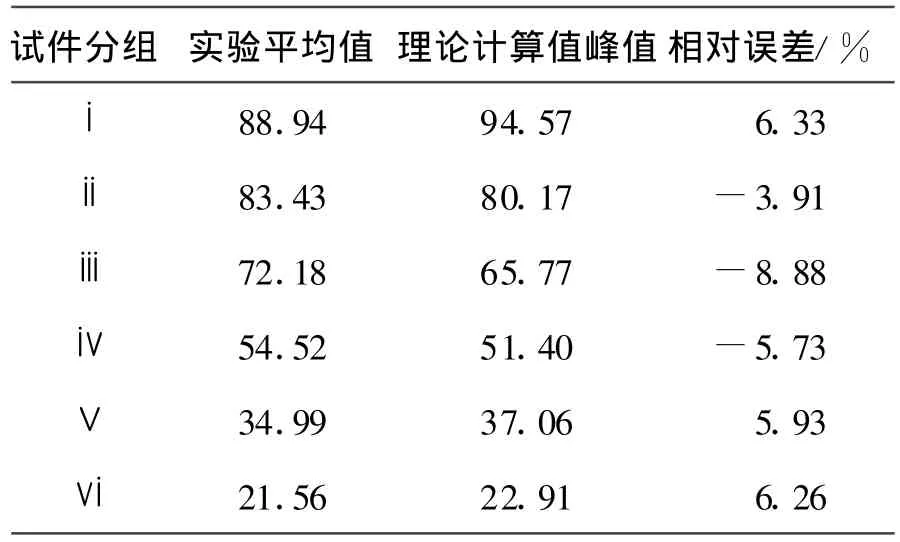
表2 理論預測峰值與實驗最大值平均值的相對誤差表
4 結論
通過對大尺寸混凝土緊湊拉伸試件的實驗結果進行應力強度因子和承載力的分析得出以下結論:
(1)由于緊湊拉伸構件尺寸的變化,其應力強度因子的實驗值存在尺寸效應;
(2)通過雙K準則和裂紋黏聚應力強度因子的關系,得到載荷與裂紋擴展長度的關系式;由預制裂紋長度能夠計算出該類構件的結構承載力,其理論結果與實驗結果基本符合.
[1] 王利民,徐世烺,任傳波.黏聚裂紋阻抗的彎曲梁承載力[J] .中國工程科學.2007,9(2):30-35.
[2] 徐世烺,趙國藩.混凝土斷裂力學研究[M] .大連:大連理工大學出版社,1991:97-115.
[3] Xu Shi Lang,Reinhardt H W.Determination of double-K criterion for crack propagation in quasi-brittle fracture[J] .International Journal of Fracture,1999,98(2):111-149,151-177,179-193.
[4] 孫啟林,王利民,韓昌瑞,等.早齡期鋼纖維混凝土抗裂性能測試與計算.混凝土,2006(8):25-27,55.
[5] Issa M Aetal.Size effects in concrete fracture,Part I:experimental setup and observations[J] .International Journal of Fracture,2000,102(1):1-24.
[6] Bazant Z P,Chen E P.Scaling of structural failure[J] .Appl.M ech.Rev.1997,50(10):593-627.
[7] 趙建生.斷裂力學及斷裂物理[M] .武漢:華中科技大學出版社,2003.
[8] 范天佑.斷裂理論基礎[M] .北京:科學技術出版社,2003.
[9] 陳篪,蔡其鞏,王仁智.工程斷裂力學[M] .北京:國防工業出版社,1977.
[10] 王利民,徐世烺,趙熙強.考慮軟化效應的黏聚力裂紋張開位移分析[J] .中國科學(G),2006,36(1):59-71.

