基于確定當量的風險規避零售商最優訂貨決策分析

鄧景毅，張小康 DENG Jing-yi,ZHANG Xiao-kang

（1.暨南大學 管理學院，廣東 廣州 510632；2.廣東商學院 信息學院，廣東 廣州 510320）

供應鏈是由供應商、零售商及用戶構成的網絡，其目的是實現整體最優，避免因局部理性造成的全局效率下降。在供應鏈網絡上的各實體之間建立契約關系是的重要手段之一，包括批發價格契約、數量彈性契約、收入共享契約、銷售回扣契約、回購契約等[1-5]。目前，大部分的供應鏈契約理論都是以報童模型為基礎，并且進一步發展該模型。報童模型的假設之一是：供應鏈實體 （agent）是風險中性的——各實體的目標是收益最大化。但是，現實中的實體并不都是風險中性的，它們可能存在各種風險偏好，既可能是始終規避風險或者趨向風險的，也有可能是在收益低時趨向風險而收益高時規避風險。不少文獻對實體風險偏好進行了研究，其中既有對供應鏈中的單個實體決策進行研究的成果 （如文獻[7,8,12]等），也有對整個供應鏈中存在風險偏好實體時如何進行協調的研究成果 （如[9,15]等）。其中，Lau等 （1999）應用方差，對原有的收益函數進行修正，進而確定供應商的定價策略[7]。Agrawal等 （2000）研究了價格隨需求發生變化的風險規避零售商的訂貨決策問題[8]。Gan等 （2004）則在原有的收益函數基礎上，將方差作為求解最大收益的約束條件，探討了風險規避實體的供應鏈協調問題[9]。國內不少學者也在供應鏈的風險研究方面作了有益的探索，包括葉飛 （2006）和于春云 （2007）等[10-11]。總的說來，對單個實體風險偏好研究較多，而對整個供應鏈的風險偏好問題研究的較少 （或者說是：供應鏈中包含一個或者多個風險偏好實體的協調問題），但前者是后者的基礎。在批發價格契約基礎上建立的報童模型，風險主要由零售商承擔。因此，本文以供應鏈中零售商的訂貨決策為主要研究對象。

1 問題的提出

不論是研究單個實體的風險偏好還是研究整個供應鏈在風險偏好下的協調問題，供應鏈實體風險偏好研究的核心在于：應用何種風險度量模型以何種方法對實體的風險偏好進行處理。歸納目前的文獻，采用的風險度量模型包括：均值－方差模型、指數模型、CVaR模型等；風險對實體決策的影響處理方法包括：最大效用法[12]、確定當量方法、約束條件法、收入函數修正法等。最大效用法直接應用效用最大化為依據進行決策，該方法的決策結果直接與選取的效用函數相關，還與效用的初始值等因素相關[12]。約束條件法要求收益方差不大于某一方差閾值δ，但是從文獻[8,10]等可以看出，該方差是一個絕對值，它的大小取值與收益的大小是相關的，即收益大時，即使方差較大也可能被風險規避者接受。因此，在實際應用中，閾值δ的取值較難確定。收入函數修正法也采用方差進行分析，所不同的是其將δ與系數k相乘后直接代入收益函數進行分析[7]，該方法中，系數k的取值與風險偏好相關，但是其取值的邏輯依據以及k是否是一個常數值得商榷。

確定當量法由Simon和Theil提出，用于動態理性期望模型分析，其在資本預算領域中廣泛采用，是進行風險處理的有效方法[13－14]，在文獻[14]中對確定當量法的應用進行了詳細描述。確定當量法的優點在于引進風險偏好的同時，仍然采用收益最大法進行決策分析，這樣就保證了與風險中性分析的一致性，便于比較研究；而且，其采用的當量處理可以部分減少效用函數選取對決策值的影響 （通過取效用函數的反函數實現），而保留風險偏好的影響，因此它是一種較好的風險研究方法。利用確定當量法處理供應鏈風險問題在國內尚未見到相關文獻。本文采用指數效用模型對風險進行定量，利用確定當量法對風險進行處理，并且數學證明了，風險規避將使得零售商訂貨量下降；風險規避系數越大，訂貨量下降越多。通過數值實驗，比較了不同風險規避系數下，零售商的最優訂貨量。

2 模型的基本描述與構造

考察由一個供應商和一個零售商組成的二階段供應鏈系統。供應商提供單一商品，在銷售季節開始前，零售商下達訂貨單，供應商收到訂單后組織生產并且發貨。零售商在每個銷售季節開始前只有一次訂貨機會，向供應商提交訂貨數量Q，中間不能補充訂貨。市場需求D是一個非負、連續型的隨機變量，其分布函數為F（x ），密度函數為f（x），并且滿足IGFR條件 （Increasing Generalized Failure Rate，正態分布、指數分布、威布爾分布等均滿足該條件）。供應商依據訂貨量進行生產，生產成本為c，并且以批發價格w出售給零售商。零售商在獲得商品后將再次出售，售價為p，p＞w＞c。若商品在該銷售季節內未被出售，其殘值為v，c＞v。為簡化模型，不考慮缺貨成本，這意味著供應鏈的風險全部由零售商承擔，而供應商不承擔風險。

根據已知條件，分析可知，供應商的收益為：

零售商的收益為：

供應鏈的收益為：

在滿足供應鏈收益最大的條件下，對 （3）求導，可得：

其中， F－1（·）是F（x）的反函數，Q*是供應鏈收益最大時訂貨量的取值。

2.1 風險中性下，零售商的訂貨決策

當零售商為風險中性時，零售商的決策依據是收益最大化，即 （2）式取最大值。 （2）式對Q求導，可以得到：

由于增函數的反函數也是增函數，所以，可對式 （5）進行變換可得：

由 （6） 式和 （2） 式，可以得到：

對 （7）式求導，得到：

由上式可知，在風險中性下，零售商的利潤隨著訂貨量的增加而增加。

由 （6） 式和 （3）式可以得到：

文獻[3]利用價格彈性證明了式 （9）是單峰的，πsn存在最大值，此時

2.2 風險規避下，零售商的訂貨決策

指數效用函數是在處理風險和效用問題時常用的經濟學模型。假設零售商具有如下的效用函數：

k＞0，稱為風險規避因子，k越大，實體對風險越厭惡；R表示收入。由于U'/U"是一個常量，因此，在U的有效定義域內，實體對風險的容忍程度保持不變。

由（2）式可知，當市場需求在x∈[0,Q)時，零售商的收入可以表示為：p－（）v x；當市場需求在x∈[Q,+∞)時，零售商的收入可以表示為：p－（）v Q。因此，零售商的期望效用可以表示為：

由 （2）式和 （13）可知，風險規避零售商的收益為：

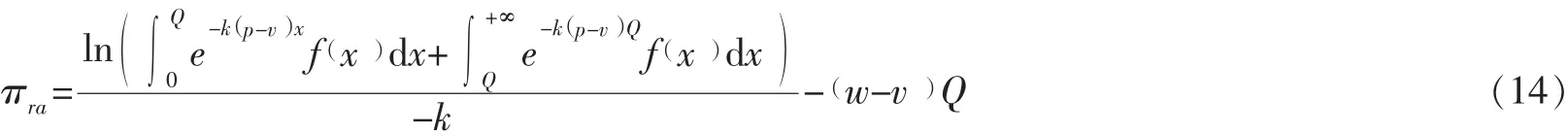
對風險規避零售商的收益函數取最大值，可以得到，此時的最優訂貨量為：

（15）的存在性證明見下文。

對于 （14）式，進一步分析可以得出以下結論。

命題1對于給定的w，風險規避零售商的收益為凹函數。

證明：式 （14）對Q取一階和二階導，可得：

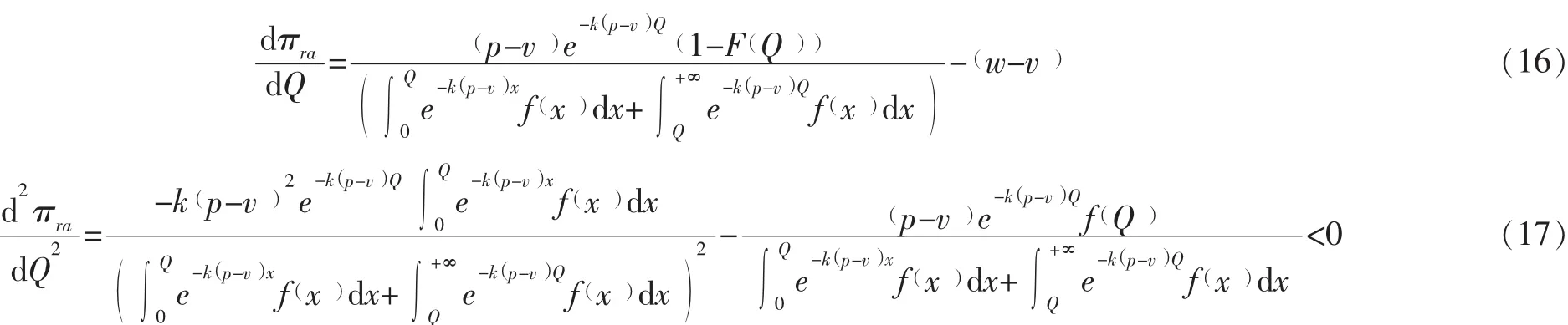
命題得證，也就證明了 （15）式成立。

命題2對于給定的w，Qa＜Qn。

證明：若Q＝0，顯然對于式 （16）有：

對于給定的w，風險中性零售商的最優訂貨量Qn滿足式 （5）。由式 （5）和式 （16）得到：

依據式 （17）、 （18）、 （19） 式以及拉格朗日中值定理可知， 在 ［0, Qn］之間存在Qa使得 πra取最大值。 因此，風險規避零售商將選擇較風險中性零售商更小的訂貨量，這符合實際，與直覺吻合。同時，也從側面證明了模型的合理性。

命題3對于不同的風險規避因子k1,k2，若存在k1＜k2，則它們所對應的最優訂貨量存在如下關系：其中表示風險規避因子為ki時的零售商最優訂貨量。

變換可得：

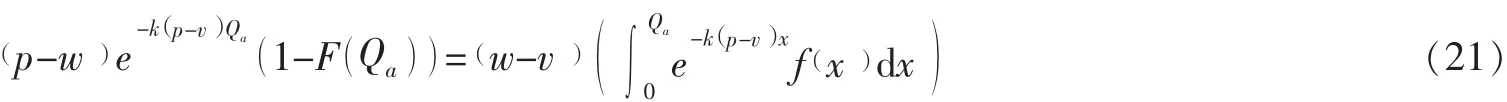
式 （21）對k求導，可以得到：

3 數值實驗

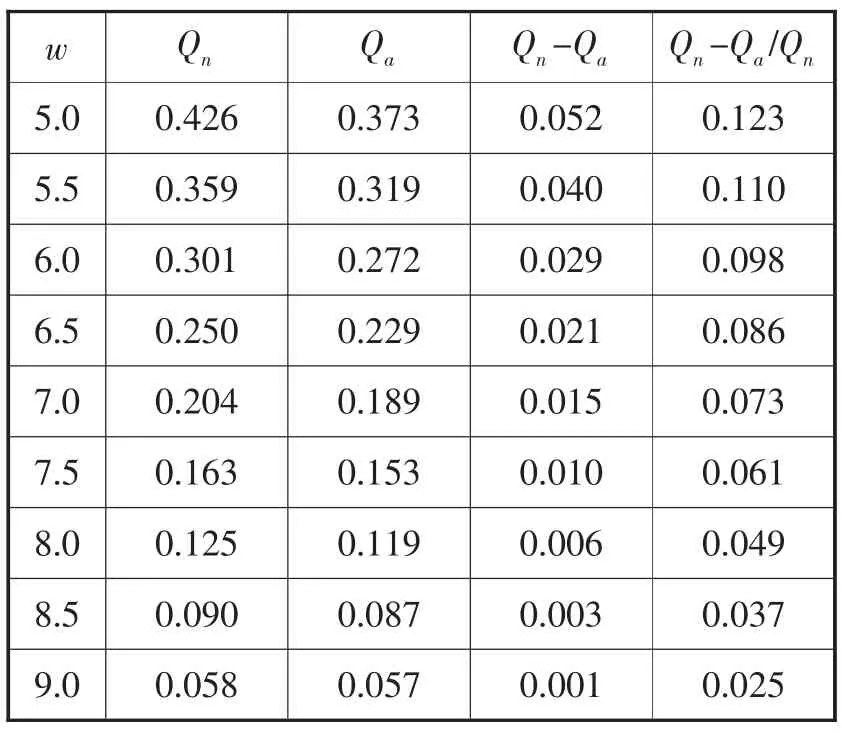
表1 不同批發價格下，Qa和Qn的比較

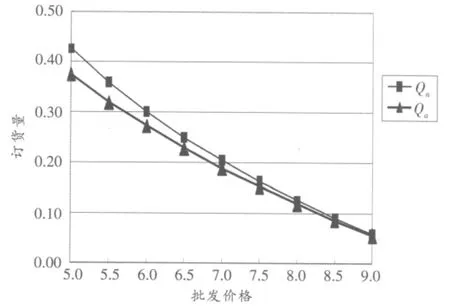
圖1 最優訂貨量隨批發價格的變動

由圖1可看出，風險規避零售商的最優訂貨量較風險中性零售商的訂貨量小，兩者之間的差值隨著批發價格的上升而下降。這一現象可以將市場需求的密度函數帶入式 （16）而得到數學上的解釋。更為直觀的解釋是：由于批發價格的上升，Qn和Qa均減小，但是由于Qn是風險中性下的訂貨量，其減小的速率更快些，從而使兩者的差值及其比率越來越小。

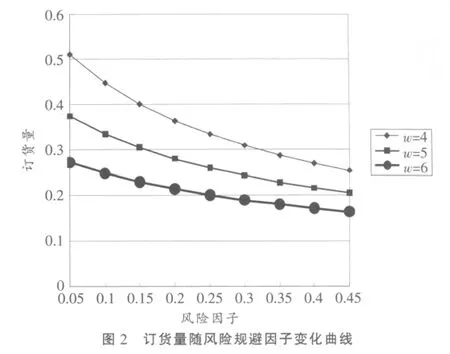
當批發價格確定時，零售商的訂貨量將隨著風險規避因子的變化而發生變化，見表2和圖2。

由圖2可以看出，隨著風險規避因子的不斷增加，零售商的訂貨量不斷減少。當w=4時，如果風險因此由0.05上升至0.45，訂貨量Qa下降超過50%。而根據負指數效用函數理論，當風險規避因子達到0.45時，已經對風險相當厭惡了。同時，也可以發現，w越小，曲線的曲率越大，說明在w較小時，風險規避因子對訂貨量影響比較大。

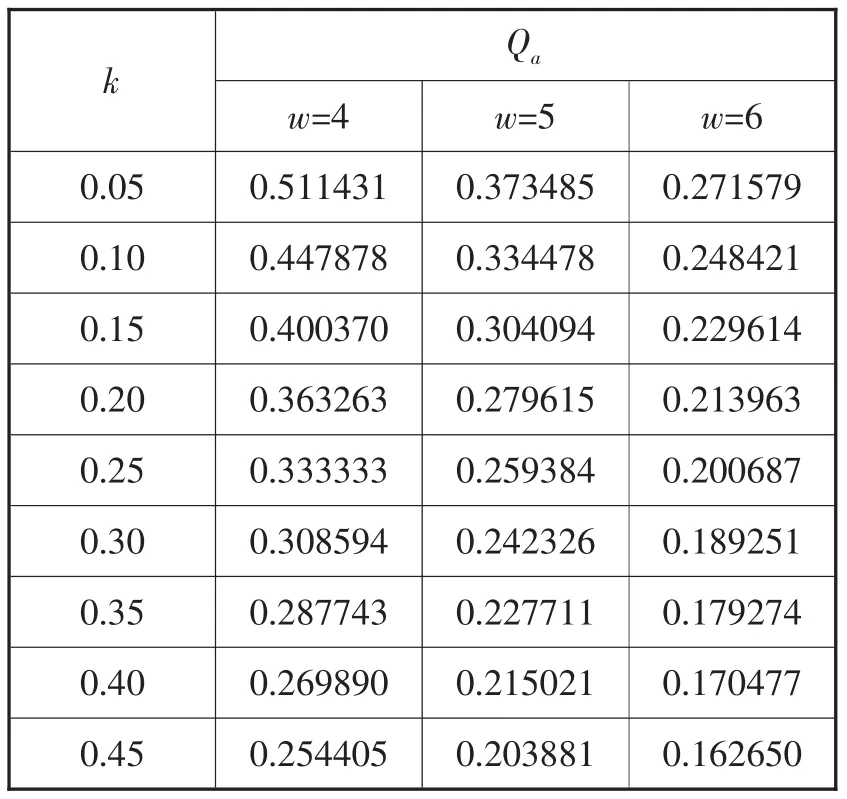
表2 風險規避因子對Qa的影響

4 總 結

模型的作用在于簡化系統內部各要素之間的聯系，以便于分析問題，抓住事務的主要矛盾。建立模型后，應該不斷對模型進行修正，以使得模型能夠更好的預測現實世界。風險中性假設與現實并不吻合，將風險因素引入供應鏈模型是必要的。負指數效用函數在風險定量研究中有著廣泛的應用。通過確定當量法，將期望效用值轉化為確定效用值，從而將風險因素引入零售商收益函數進行分析和處理，進而計算出零售商的最優訂貨量這是一種有效供應鏈分析方法。供應商在確定零售商為風險規避者時，將如何進行決策是我們進一步的研究方向。

[1]B.Pasternack.Optimal Pricing and Returns Policies for Perishable Commodities[J].Marketing Science,1985(4):166-176.

[2] A.Tsay.Quantity-Flexibility Contract and Supplier-Customer Incentives[J].Management Science,1999,45(10):1339-1358.

[3] Selling to the Newsvendor.An Analysis of Price-Only Contracts[J].Manufacturing&Service Operations Management,2001,3(4):293-305.

[4] T.Taylor.Supply Chain Coordination under Channel Rebates with Sales Effort Effects[J].Management Science,2002,48(8):992-1007.

[5]P.Cachon,A.Lariviere.Supply Chain Coordination with Revenue-Sharing Contracts:Strengths and Limitations[J].Management Science,2005,51(1):30-44.

[6] G.Perakis.The Price of Anarchy in Supply Chains:Quantifying the Efficiency of Price-Only Contracts[J].Management Science,2007,53(8):1249-1268.

[7] H.Lau,A.Lau.Manufacturer’s Pricing Strategy and Return Policy for a Single-Period Commodity[J].European Journal of Operational Research,1999(116):291-304.

[8] V.Agrawal,S.Seshadri.Impact of Uncertainty and Risk Aversion on Price and Order Quantity in the Newsvendor Problem[J].Manufacturing and Service Operations Management,2000,2(4):410-423.

[9] X.Gan,S.P.Sethi,H.Yan.Coordination of Supply Chains with Risk-Averse Agents[J].Production and Operations Management,2004,13(2):135-149.

[10] 葉飛.含風險規避者的供應鏈收益共享契約研究[J].工業工程與管理，2006(4):50-53.

[11] 于春云,等.具有風險規避者和偏愛者加盟的供應鏈優化與協調模型[J].系統工程，2007,25(1):13-20.

[12] L.Eckhoudt,C.Gollier,H.Schlesinger.The Risk-Averse （and Prudent） Newsboy[J].Management Science,1995,41(5):786-794.

[13] L.P.Hansen,T.J.Sargent.Certainty Equivalence and Model Uncertainty[C]//Board of Governors of the Federal Reserve System Proceedings,2005:17-38.

[14] R.L.Keeney,H.Raiffa.Decisions with Multiple Objectives:Preferences and Value Tradeoffs[M].Cambridge University Press,1993.

[15] V.Agrawal,S.Seshadri.Risk Intermediation in Supply Chains[J].IIE Transactions,2000(32):819-831.