滾動軸承故障診斷的改進小波變換譜峭度法
沈金偉,石林鎖
(第二炮兵工程學院 五系,西安 710025)
采用傳統的包絡分析方法進行故障診斷,結果與操作者的經驗或掌握的歷史數據緊密相關。因此文獻[1]提出了基于譜峭度的改進包絡分析法,此方法有效地實現了符合最佳包絡的頻帶的自動檢測,并在實際工作中得到了檢驗,但是其只研究了一組Morlet復小波濾波器組,沒有深入研究多組濾波器組比較下的最優結果。文獻[2]對其進行了改進,設計了多組Morlet復小波濾波器組,每一組的濾波器數目不同,將這些濾波器組應用到故障檢測中,選出最大譜峭度對應的最優Morlet復小波濾波器,利用此濾波器對原始信號的濾波結果,得到包絡分析結果,最終檢測故障頻率。需要指出的是由此法得到的最大譜峭度是出現在每倍頻程六個濾波器的條件下,比文獻[1]采用的五個濾波器的情況結果更優。
雖然文獻[1-2]都采用了小波變換譜峭度法尋找最大譜峭度,進而找到對應的最佳Morlet復小波濾波器及其濾波信號,并且取得了理想結果,然而此方法是在人為選取多組Morlet復小波濾波器的基礎上進行的,要真正找到最優濾波器仍需在此基礎上再比較更多組濾波器組,過程很繁瑣。考慮到譜峭度與構造最優匹配濾波器之間有著密切的關系[3-4],在總結前人研究的基礎上,將譜峭度構造最優濾波器的特性與基于Morlet小波分解求譜峭度的方法結合起來,并由此取得了比原方法更加優良的檢測和診斷性能。
1 譜峭度與改進小波譜峭度法的實現
1.1 譜峭度與基于譜峭度的最優匹配濾波器
不同的小波函數具有不同的時頻結構,考慮到故障軸承所產生的暫態沖擊振動響應成分,可以發現Morlet復小波能夠最好逼近此類尖銳變化的信號,因此一般選用Morlet復小波對原始信號進行小波變換[1]。
為了最大限度地發揮Morlet復小波作為一個濾波器組的特點,同時為了使信號的時域和頻域表示能得到很好對應,就有必要設計多個濾波器組,且每個濾波器組的每倍頻程上的濾波器數目應不相同[2]。
譜峭度是在峭度的概念上發展起來的一個時頻域檢測指標,應用于機械故障診斷的基本原理是將故障信號經過時頻分解得到其時頻域分布,而后在每一個頻帶上計算信號的時域峭度,因此其對暫態沖擊成分十分敏感,通過分析不同頻帶上的峭度值即可指示出故障的存在,實現早期故障診斷。文獻[3-4]對其有一個比較詳細和系統的定義:
(1)
式中:C4Y(f)為過程Y(t)的4階譜累計量;S(f)為譜瞬時矩。根據此方法定義的譜峭度具有很多重要的性質[3],在此需要用到的性質是:對于一個CNS過程z(t)=y(t)+n(t)(其中n(t)是與信號y(t)相互獨立且平穩的高斯噪聲信號),則其譜峭度為:
(2)
式中:ρ(f)=S2N(f)/S2Y(f),代表信噪比,是頻率的函數。值得指出的是,在ρ(f)很大的地方過程的譜峭度值接近于0,而在ρ(f)很小的地方其值近似等于KY(f),因此通過搜索整個頻域,可以找到譜峭度最大的頻帶,即為故障頻帶,這也表明了譜峭度對與檢測故障的優越性。由(2)式發現了譜峭度與最優匹配濾波器設計之間的關系,即:
(3)
將(2)式代入(3)式得:
(4)
式中:k為未知參數,其獲取可以先假設一個比較小的值代入(4)式,構造最優匹配濾波器,而后通過多次迭代找到使濾波器濾波后相應輸出信號的峭度值最大的k值,從而確定參數k。應用此濾波器可以使y(t)*m(t)與n(t)*m(t)功率比達到最大,即實現信噪比最大化。根據暫態波形是確定的還是隨機的,相應的有兩種構造方法[4]:
(1)波形確定的情況下,可直接通過(4)式進行構造。
(2)波形隨機的情況下,利用(4)式的逆Fourier變換組成一自相關陣,通過求自相關陣給出的最大特征值所對應的特征向量,去構造相應的最優匹配濾波器。
事實上,一般都認為波形是隨機的,所以都按(2)的情況構造。
基于濾波器對譜峭度的依賴,必須首先選用時頻分解得到譜峭度值,考慮到Morlet復小波在已有小波函數中最逼近軸承振動沖擊信號[1],因此選用了基于Morlet復小波的小波變換,但Morlet復小波是事先人為確定的,相比之下根據譜峭度構造的最優匹配濾波器則應該更具有靈活性和匹配特性。為了驗證此結論,在原有小波變換譜峭度法的基礎上做了相應改進。
1.2 改進小波譜峭度法的實現
(1)設計Morlet復小波濾波器組,相關參數如下[2]:
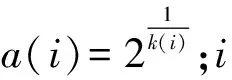
②Q=2/k(i);使每個濾波器的帶寬等于各個濾波器之間的間隔。
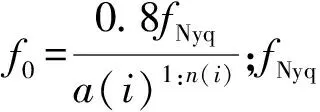
④帶寬σ=Q×f0;一旦這些參數得到確定,就可以生成需要的濾波器組。
(2)將原始信號的FFT與濾波器組矩陣的每一行相乘,然后對結果進行IFFT運算得到小波系數。
(3)將小波系數與其復共軛做乘積得到濾波后信號的時域平方包絡。
(4)根據(1)式定義計算相應的譜峭度值。
(5)利用求得的譜峭度值,根據上述方法構造匹配濾波器,對此原始信號進行濾波,并作平方包絡分析,得到其包絡譜,進行故障識別和診斷。
2 改進小波變換譜峭度法在仿真信號中的應用
本文采用文獻[5]的故障仿真信號,用一個單自由度彈簧-質量-阻尼振動系統模擬軸承局部故障產生的振動沖擊,并在沖擊的時間間隔上引入了微小的隨機變化,以更好逼近實際信號。其故障特征頻率為200 Hz,共振頻率為9 000 Hz,采樣頻率為32 768 Hz。下面利用該仿真信號來對比檢驗強噪聲背景下小波變換譜峭度法與改進小波變換譜峭度法的檢測性能。
圖1和圖2顯示對混入能量為32 dB的高斯白噪聲的仿真信號應用小波變換譜峭度法和改進小波變換譜峭度法后得到的平方包絡譜圖,可以看到,當噪聲干擾不是很大的時候兩者的檢測效果基本一致,都能精確檢測出200 Hz的故障頻率。
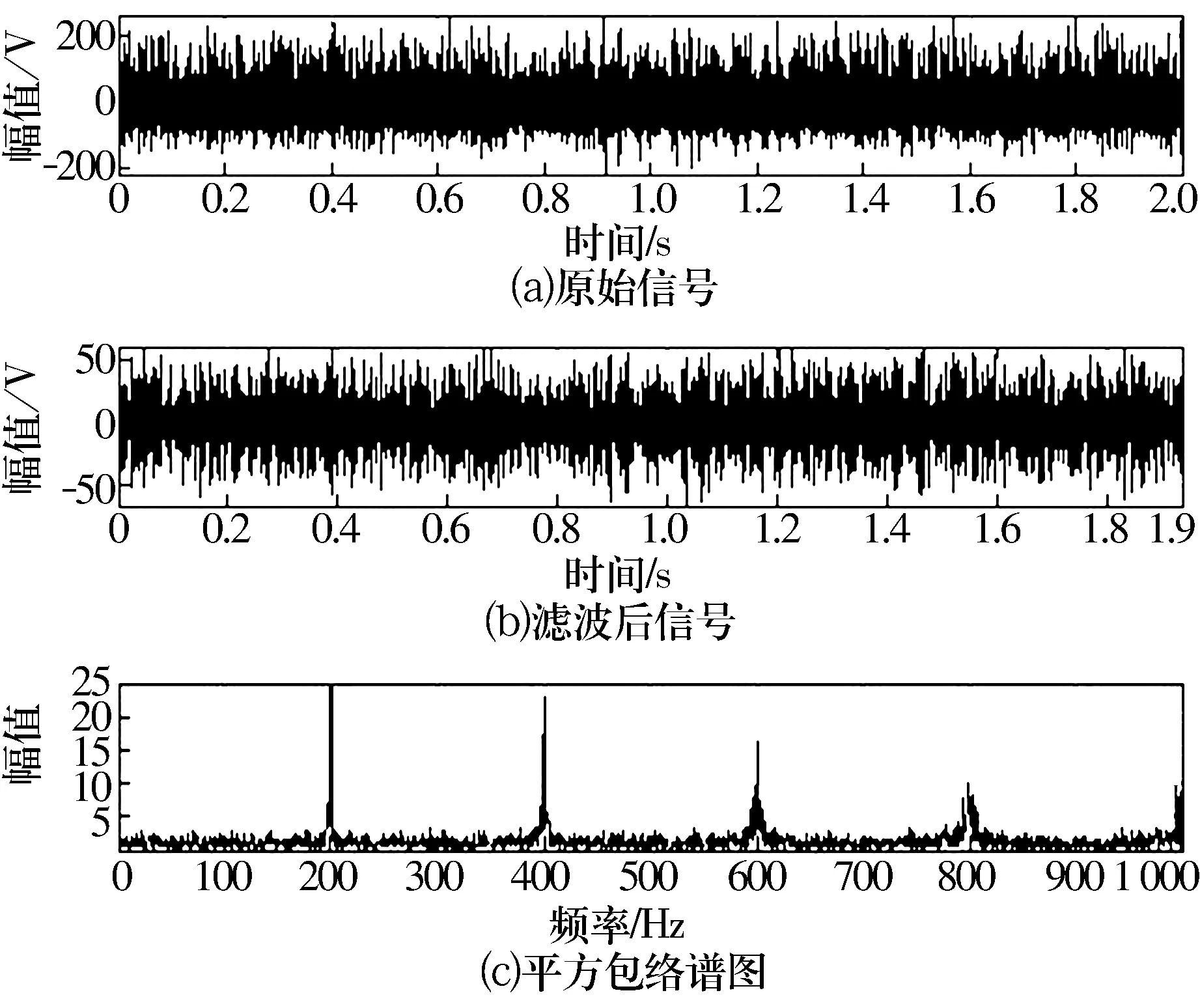
圖1 基于Morlet小波濾波的小波變換譜峭度法結果
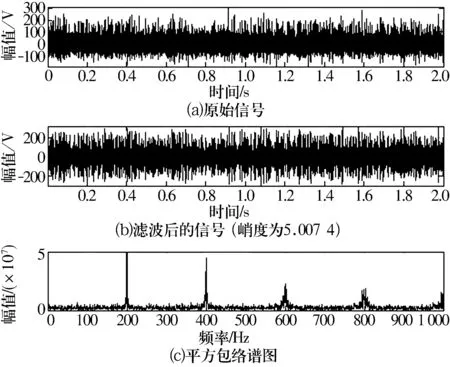
圖2 使用匹配濾波器濾波后的小波變換譜峭度法結果
為了更好地比較兩者的有效性,將噪聲能量提高到40 dB,該條件下最優匹配濾波器見圖3。試驗結果見圖4和圖5,由圖可知,基于Morlet小波濾波的小波變換譜峭度法已經無法檢測出故障(事實上研究結果表明當有能量高于35 dB的噪聲干擾時此方法已基本失效),而改進的小波變換譜峭度法仍能很好地檢測出200 Hz的故障頻率,而且還能適應噪聲能量更高的噪聲環境。
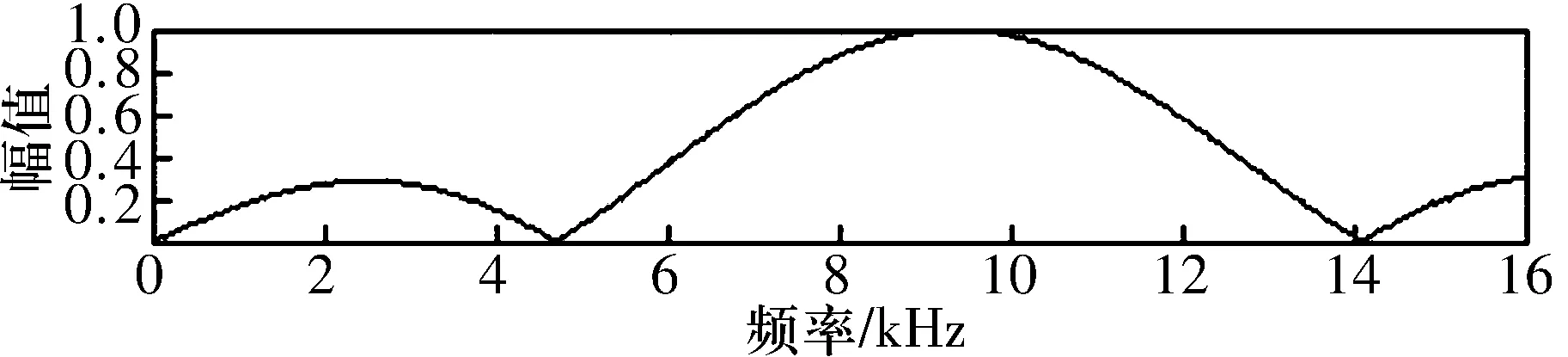
圖3 混入能量為40 dB的噪聲條件下的最優匹配濾波器
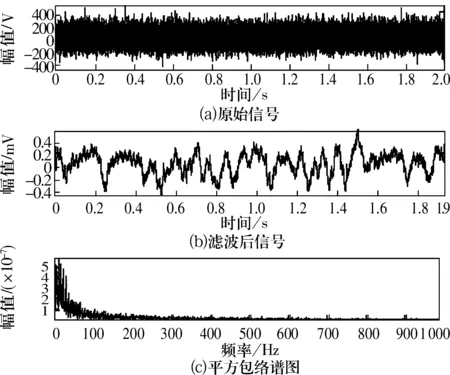
圖4 基于Morlet小波濾波的小波變換譜峭度法結果
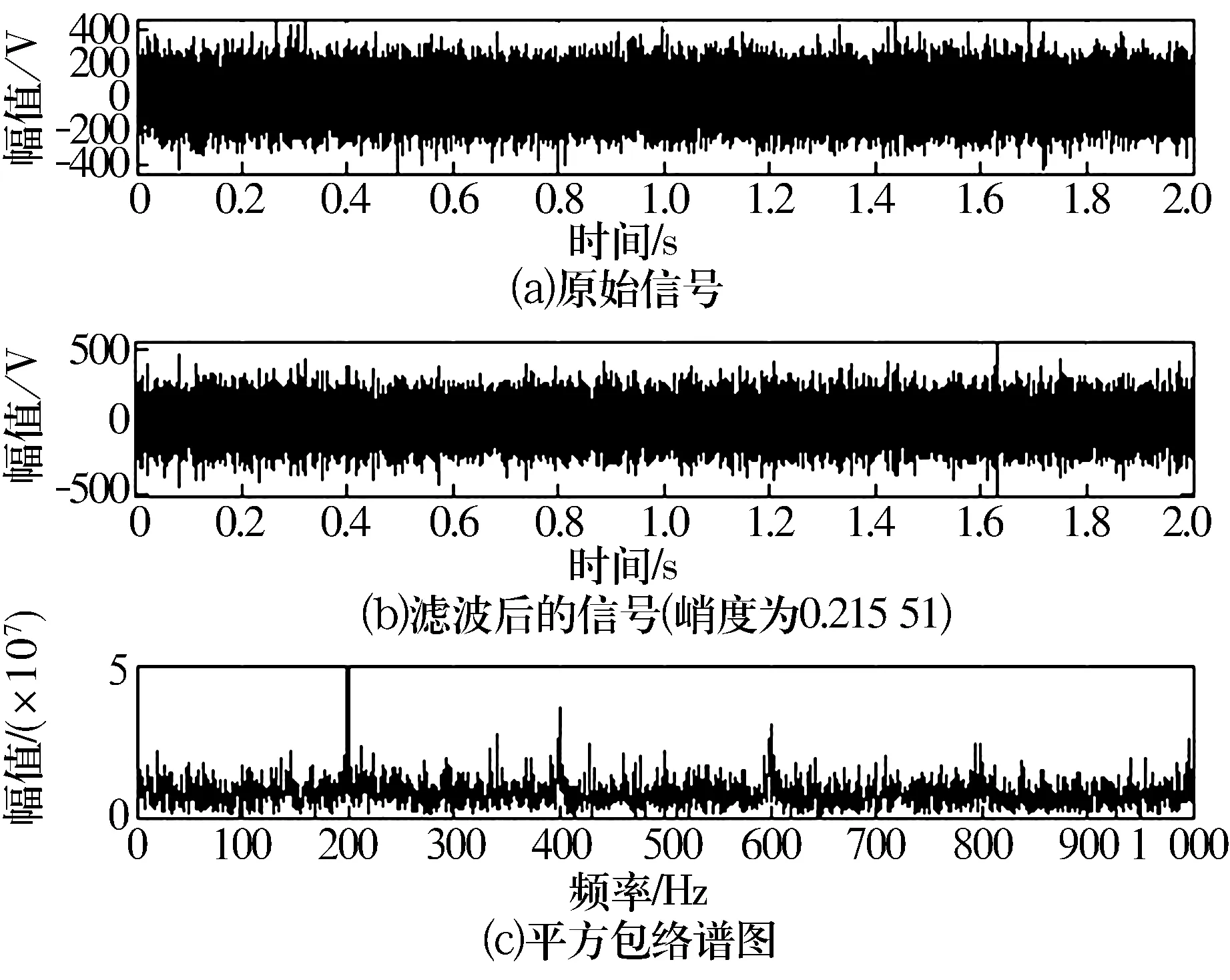
圖5 使用匹配濾波器濾波后的小波變換譜峭度法結果
由以上比較分析可知,強噪聲背景下,改進的小波變換譜峭度法具有更強的適應能力和檢測效果。
3 改進小波變換譜峭度法在實測信號中的應用
實際信號采自安裝在一個變速箱中存在內圈點蝕故障的滾動軸承,變速箱軸的轉速fr=10 Hz,鋼球個數Z=12,鋼球直徑Dw=7.12 mm,球組節圓直徑Dpw=38.5 mm,接觸角φ=0,采樣頻率為4.8 kHz。根據平穩工況條件下軸承內圈故障特征頻率計算公式可知其內圈故障頻率為71.1 Hz。下面用改進方法來檢測此故障。
首先計算其譜峭度值,并構造匹配濾波器。圖6、圖7分別為快速譜峭度圖[6]和構造的匹配濾波器單邊譜圖。
圖6中縱坐標表示每倍頻程上的濾波器個數,Kmax為最大譜峭度值,fc為得到最大值時的濾波器中心頻率。將如圖7所示構造的匹配濾波器應用到實際信號中,其檢測效果如圖8所示,與仿真信號的試驗效果一致,精確地檢測出了內圈故障特征頻率71.1 Hz。
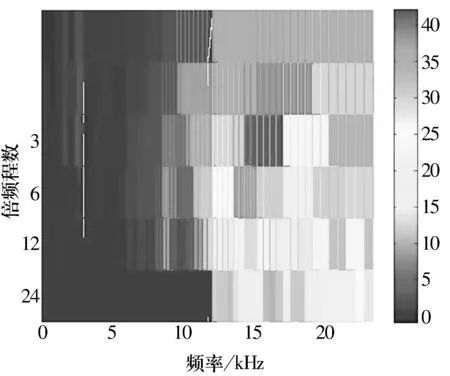
圖6 小波變換譜峭度圖
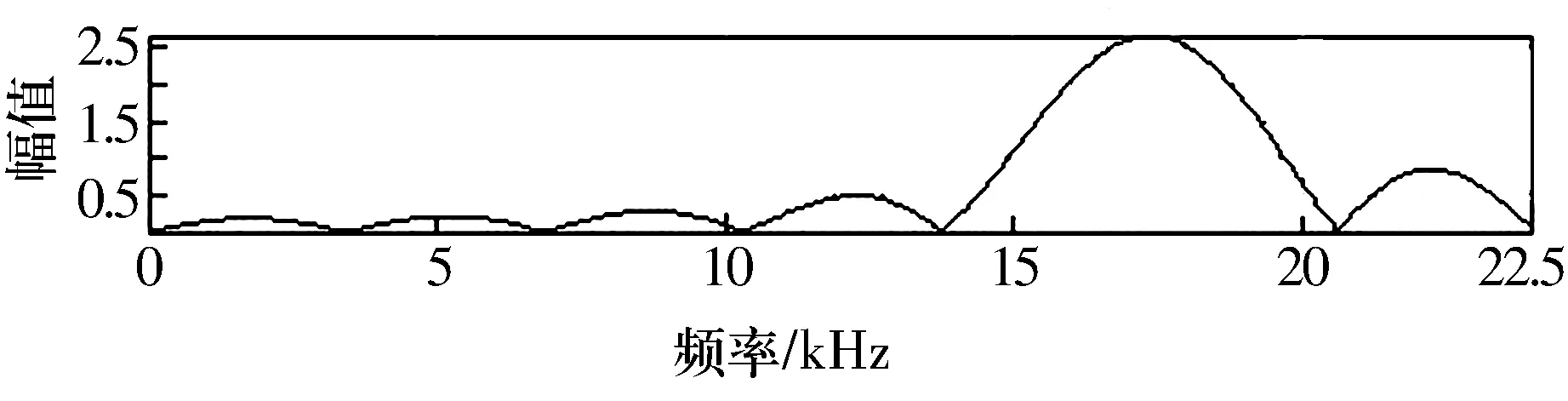
圖7 改進小波譜峭度法構造的濾波器
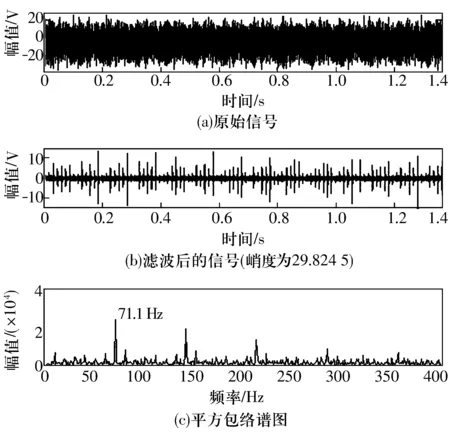
圖8 改進小波變換譜峭度法實測結果
4 結束語
在結合前人研究成果的基礎上,利用譜峭度與構造匹配濾波器之間的重要關系,對小波變換譜峭度法進行了改進。相對于Morlet小波濾波器的事先人為設計的特點,由于用譜峭度構造的匹配濾波器具有更好的自適應性和匹配特性,因此應用此匹配濾波器應該具有更強的實用性,且給出了相應的仿真效果比較,結果證明了此結論。最后將此方法應用到實測信號中,同樣取得了理想的效果。

