滾動軸承壽命與可靠性試驗的評定方法
張 偉,湯 潔,胡留現
(1.洛陽軸承研究所有限公司,河南 洛陽 471039;2.洛陽理工學院,河南 洛陽 471023)
軸承的壽命可靠性是軸承綜合質量水平的體現,是軸承的一個重要質量指標。通過軸承的壽命可靠性試驗可以反映出軸承成品以及零件的整體質量水平。軸承經過壽命與可靠性試驗后,其試驗數據如何評估,評定方法就顯得尤為重要,且評定方法必須能體現整個行業的先進水平,需要給軸承生產企業、用戶、行業及第3方認證機構一個指導性文件。
軸承行業對軸承壽命與可靠性試驗評定方法的研究已有很長時間。1985年洛陽軸承研究所首次制定了滾動軸承壽命試驗評定方法ZQ 37—85《滾動軸承壽命可靠性考核試驗方法》,后于1991年修訂為JB/CQ 37—91《滾動軸承壽命可靠性考核試驗方法》,又于1997年再次修訂為JB/T 50093—1997《滾動軸承 壽命及可靠性試驗評定方法》。
多年來,滾動軸承壽命及可靠性試驗評定方法對促進軸承壽命可靠性質量的提高、行業的質量評定以及國內、外用戶的產品驗收起到了重要的作用。為適應新形勢下軸承質量水平不斷提高的要求,以及和國外軸承質量的接軌問題,特制訂GB/T 24607—2009《滾動軸承 壽命與可靠性試驗及評定》標準,以促進軸承壽命可靠性質量進一步提高。
1 合格評定
軸承壽命可靠性試驗原始數據經數據處理后得到相關參數,對參數進行一系列評估后才能得出合格與否。
質量要求:L10t/L10h≥Z′即為合格,其中L10t為基本額定壽命的試驗值;L10h為基本額定壽命;Z′為質量系數,與軸承的結構、材料、工藝有關,球軸承Z′=1.4,滾子軸承及調心球軸承Z′=1.2。
但對具體的試驗有不同的要求,最基本的驗證試驗達到合格壽命即認為合格;而鑒定試驗要求達到合格壽命的3倍為合格。
如果是長壽命試驗時,還應給出達到合格倍數的值,即達到L10t/L10h的倍數值。
2 試驗數據處理
常規試驗數據處理一般依據二參數Weibull分布函數,使用圖估計法和參數估計法進行分析處理。其中,圖估計法較簡便直觀,一般可優先采用;而對試驗數據較少或無失效數據的情況一般采用序貫試驗評定方法。
2.1 Weibull分布圖估計法
2.1.1 圖估計目的
通過對軸承樣品的完全試驗、截尾試驗等,得出試驗數據,根據圖估計法在Weibull分布圖上估計出分布參數,并得出試驗結果及評定結果。
2.1.2 Weibull分布圖
軸承壽命服從二參數Weibull分布函數:
其對數形式為:
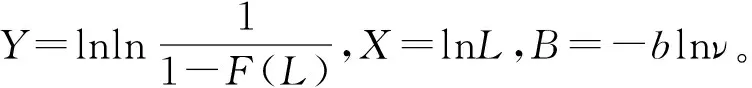
則上式變成直角坐標系中一條直線方程:
Y=bX+B。
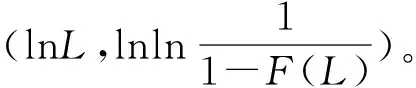
軸承壽命Weibull分布曲線是以b為斜率,ν為特征壽命的一條直線,b表示軸承壽命的離散程度或軸承壽命質量的穩定性,斜率b越大,說明軸承壽命數據較集中,軸承壽命質量穩定;反之則說明軸承壽命數據離散,軸承壽命質量不穩定。ν是當F(ν)=0.632時的軸承壽命,即破壞概率為63.2%時的軸承壽命。求出參數b,ν,直線可唯一確定。
2.1.3 一般的圖估計
一般對于失效數據不少于6個的試驗數據評定,可用圖估計方法。失效數據越少,圖估計的精度就越低。
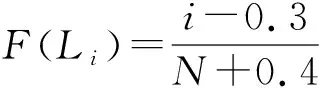
由直線求出參數b,ν,再分別求出基本額定壽命的試驗值L10t(縱軸為10%),中值額定壽命的試驗值L50t(縱軸為50%),計算出可靠度Re等。
2.1.4 分組淘汰圖估計
分組淘汰試驗方法可縮短試驗周期,但試驗風險比一般完全試驗和定時(數)截尾試驗大。試驗中,每一分組中出現一個失效樣品即停止試驗,然后用各組的最短壽命數據在Weibull分布概率紙上描點,配置直線,再由該直線求得該批樣品的分布直線。
2.1.5 圖估計實例
例1:某廠生產的深溝球軸承L10h=100 h,N=8套,試驗結束,得到8個失效數據,分別是80,110,155,170,220,240,300和380 h。用Weibull分布圖估計參數b及ν,L10t,L50t,Re等值。
(a)由8個失效數據,配置直線A(圖1)。
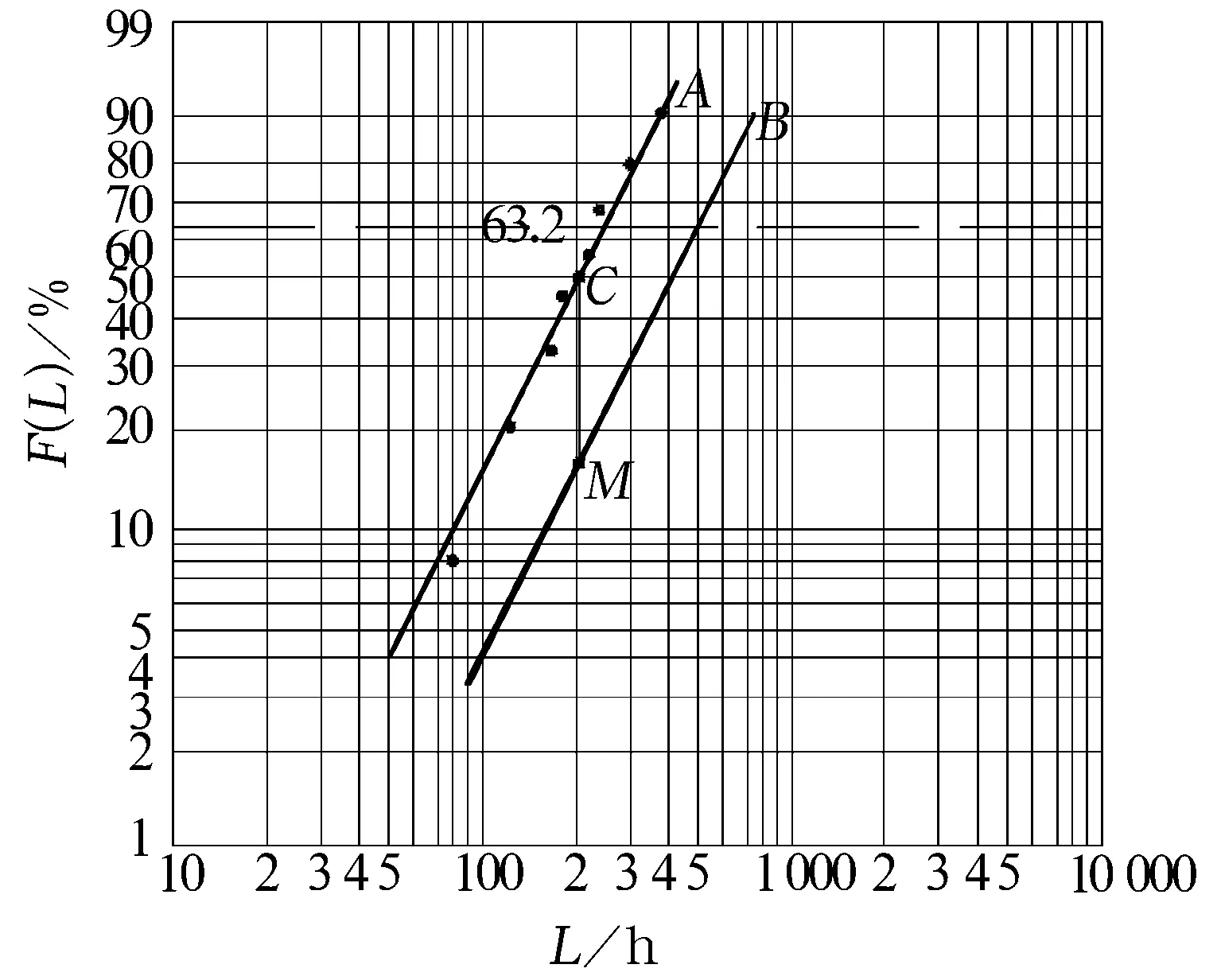
圖1 Weibull分布圖估計
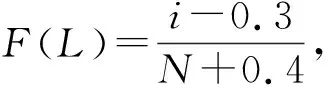
(b)由直線A求出:b=2,ν=250 h,L10t=85 h,L50t=200 h,Re=86%。
(c)L10t/L10h=85/100<1.4,故判定該批軸承樣品不合格。
例2:某廠生產的深溝球軸承L10h=100 h,N=32套,分8組(m=8),每組4套同時上機試驗N′=4套。每組有一套軸承失效即停機,試驗結束,得到8個分組的最短壽命分別為80,110,155,170,220,240,300和380 h。用Weibull分布圖估計參數b,ν,L10t,L50t,Re等值。
本例為分組淘汰圖估計例。先按例1求出分布直線A,再由分布直線A求分布直線B。
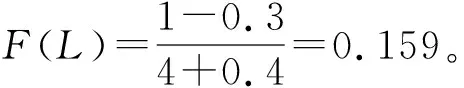
(b)作3條平行線:過F(L)=50%作橫軸平行線與直線A交于點C,過C作縱軸平行線與過F(L)=0.159的橫軸平行線交于點M。(在直線A上取縱坐標為F(L)=50%的點C,由C做縱軸平行線,并與過F(L)=0.159的橫軸平行線交于點M。)
(c)過M點做平行于直線A的平行線B。
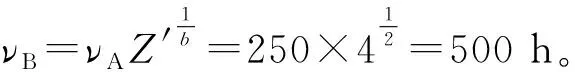
由直線B求出:b=2,ν=500 h,L10t=160 h,L50t=400 h,Re=96%。
(d)L10t/L10h=160/100>1.4,故判定該批軸承樣品合格。
2.2 Weibull分布參數估計
2.2.1 Weibull分布參數估計的目的
通過試驗軸承樣品的完全試驗、截尾試驗,得出試驗數據,根據Weibull分布數據處理估計出分布參數,并得出試驗結果及評定結果。
截尾試驗失效數據一般應不少于6個。若失效數據太少,參數估計的精度就會降低。
通過數據處理確定Weibull分布的兩個參數b,ν。
設樣本容量為N,經試驗后得到的實際壽命為:
完全試驗L1≤L2…≤Li…≤LN,i=1,2,…,N。
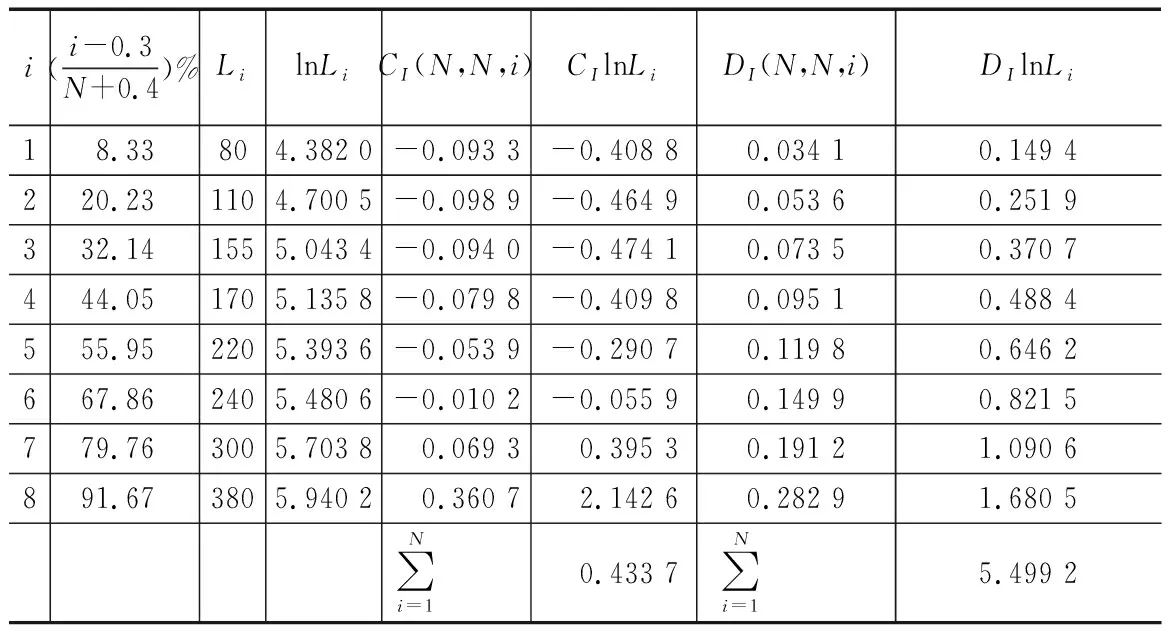
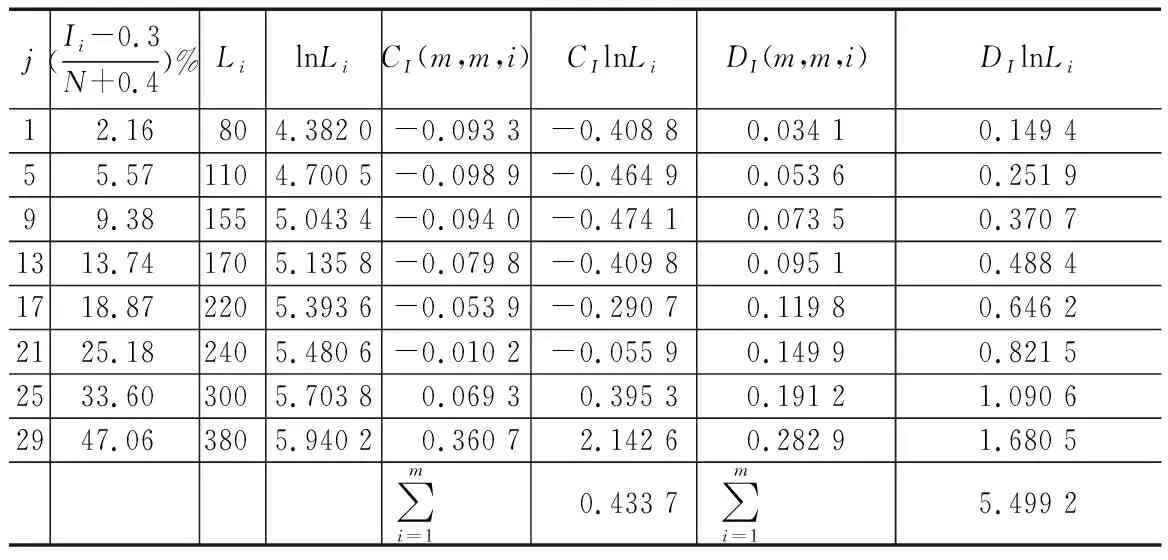
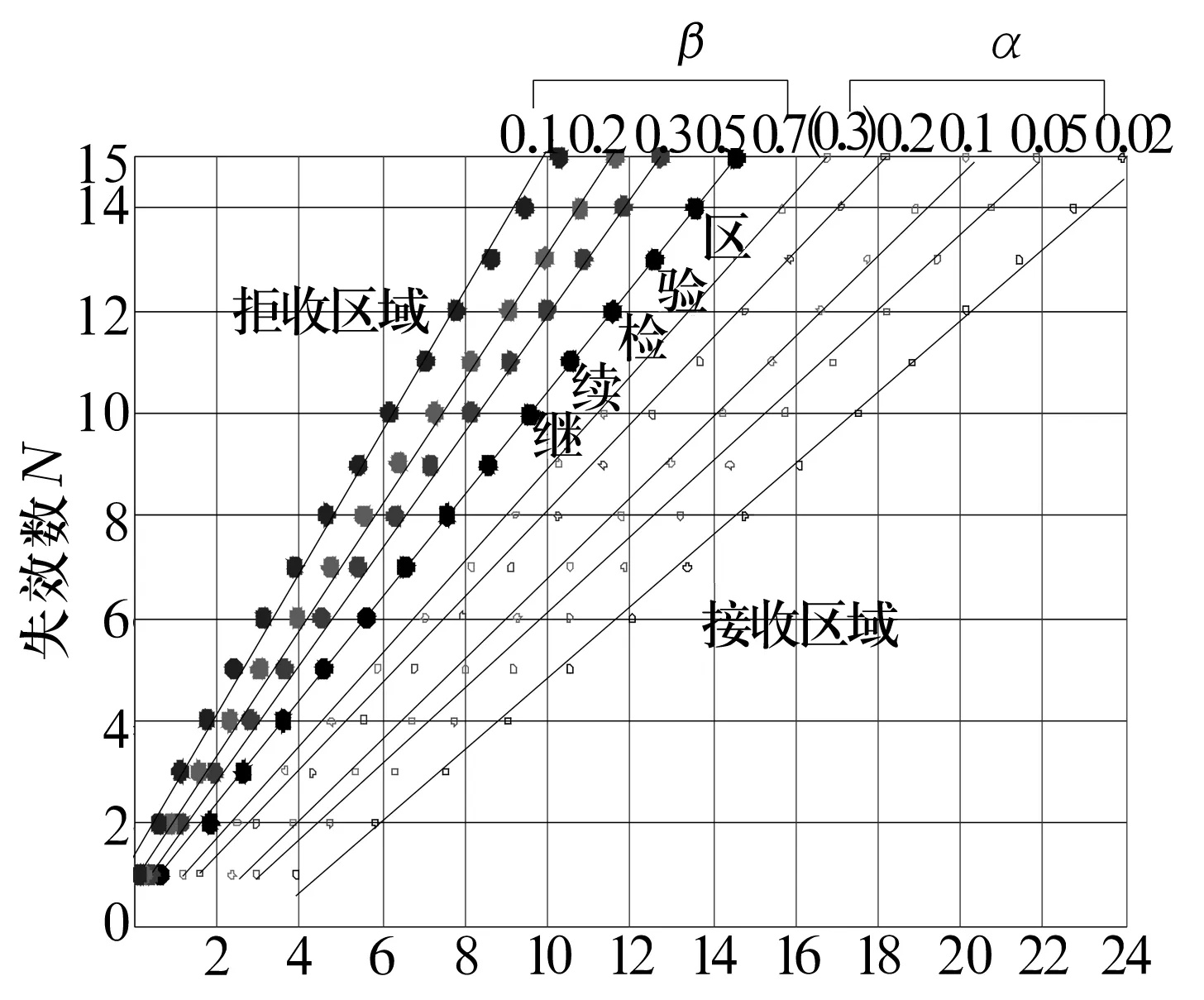
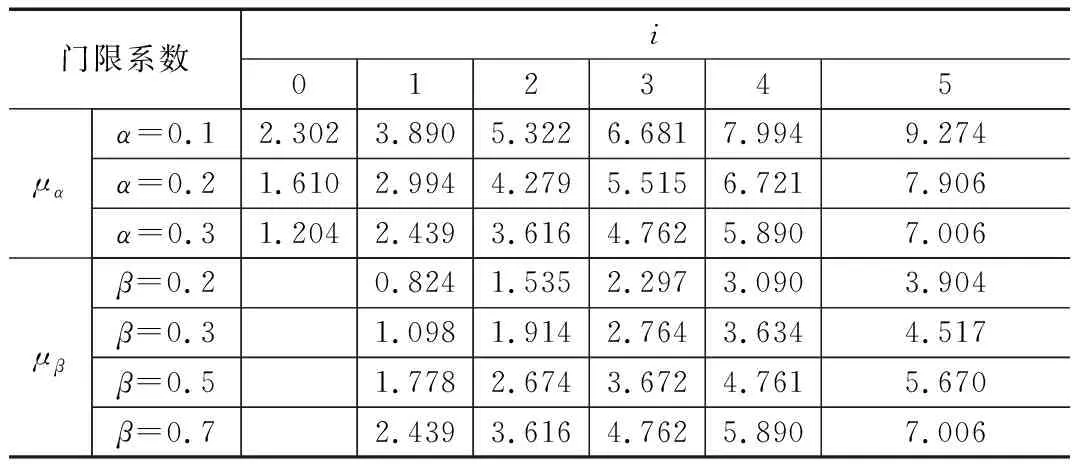
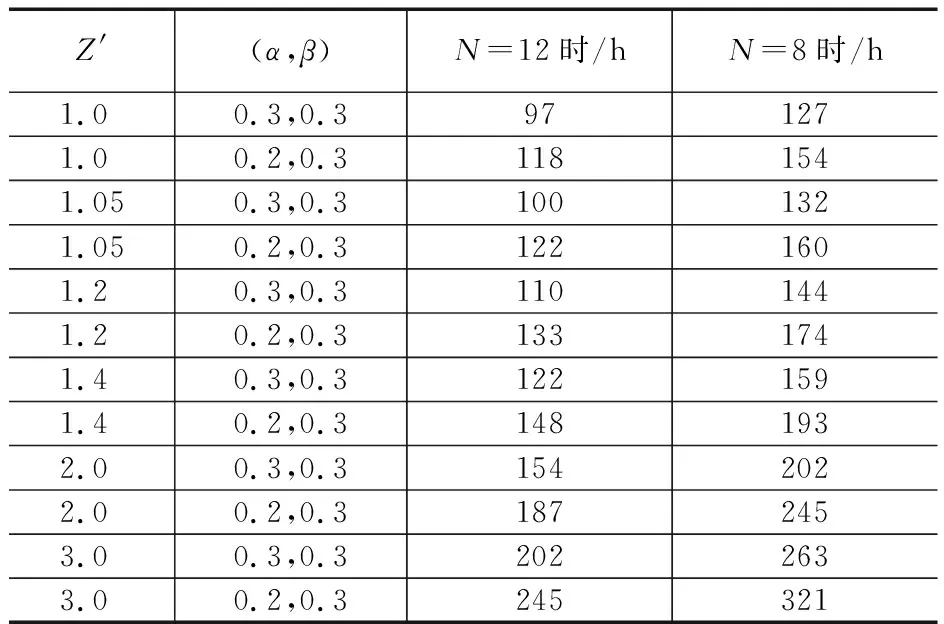
定數截尾試驗L1≤L2…≤Li…≤Lr,i=1,2,…,r;r 分組淘汰試驗L1≤L2…≤Li…≤Lm,i=1,2,…,m;m=N/N′。 表1 非完全試驗時F(Li)的修正值 軸承壽命Weibull分布參數b,ν的估計,當N≤25時,用最佳線性不變估計(BLIE)方法;當N>25時,用最大似然估計(ML)方法(略)。 2.2.2 最佳線性不變估計 完全試驗: 定數截尾試驗: 分組淘汰試驗: 最佳線性不變估計系數CI,DI見《可靠性試驗用表》。 2.2.3 依據b,ν估計L10t,L50t及Re 當F(L)=0.10時,基本額定壽命的試驗值L10t=ν(0.105 36)1/b; 當F(L)=0.50時,L50t=ν(0.693 15)1/b; 2.2.4 參數估計實例 例3:對例1的數據用Weibull分布估計參數b及ν,并計算L10t,L50t,Re等值。 本例為完全試驗,最佳線性不變估計系數為CI(N,N,i),DI(N,N,i)。 若為定數截尾試驗,失效數一般不能少于試驗樣品容量的2/3,即r 參數估計列于表2,計算得:b=2.305 7,lnν=5.499 2,ν=244.5 h,L10t=92 h,L50t=210 h,Re=88%。 表2 Weibull分布參數估計表 L10t/L10h=92/100<1.4,故判定該批軸承樣品不合格。 例4:對例2的數據用Weibull分布估計參數b及ν,并計算L10t,L50t,Re等值。 對樣本容量為N的試驗樣品進行試驗時,因為有各種各樣的原因使某一試樣中停試驗,此數據就是未失效數據(按數據大小排列,未失效數據可能在失效數據之間),一般數據處理方法是不考慮未失效數據,這樣就不能真實地反映整體的情況,影響軸承質量水平評價。所以含有未失效數據的處理要對失效數據進行位置修正。 非完全試驗F(Li)的修正值的計算見表1。最佳線性不變估計系數為CI(m,m,i),DI(m,m,i),參數估計見表3。 表3 非完全試驗Weibull分布參數估計表 b=2.305 7,lnν=6.100 4,ν=446 h,L10t=170 h,L50t=380 h,Re=97%。 L10t/L10h=170/100>1.4,故判定該批軸承樣品合格。 本標準所選取的后驗序貫抽樣檢驗方案,是序貫抽樣檢驗的一種。其適用性強,可利用原有試驗設備,特別是當疲勞破壞數據較少時,也可給出判定結論,便于考核及訂戶驗收;而且方法簡便,運算少,數據處理程序化、表格化,便于推廣應用。 完全試驗、截尾試驗一般需要較長試驗時間才能得出結果,而對小子樣失效數據、無失效數據的處理宜采用序貫試驗,較短時間就能得出結果。 序貫試驗用于試驗設計而不是試驗判定。第1套軸承如果出門,則直接判定合格;如果不入門,則判定為不合格;如果在繼續檢驗區,則用替換軸承繼續檢驗。 2.3.1 替換試驗 試驗采用有替換試驗序貫檢驗,按失效順序逐套進行檢驗判定。當有5套軸承樣品失效時停試,并做出合格與否的判定。試驗中替換軸承樣品的失效數據也參與判定。這種方法用于小子樣或無失效數據的處理。 2.3.2 檢驗判定參數 綜合國內、外資料,取Weibull分布斜率b=1.5。 檢驗水平:根據選取的α,β風險值分為4組,檢驗水平由寬到嚴。一般用戶驗收的試驗取水平Ⅰ或Ⅱ,行業及第3方認證機構的試驗取水平Ⅱ或Ⅲ,制造廠內部的試驗取水平Ⅲ或Ⅳ,如表4所示。 表4 檢驗水平 α為合格風險,接受風險或顯著性水平,1-α為置信度。 β為不合格風險,拒絕風險。本標準判定檢驗時配合α使用。有時稱β為使用方風險。 2.3.3 檢驗判定門限 不同的α,β值可以組成多個檢驗水平,圖2為不同檢驗區示意圖。由圖可以看出,水平Ⅰ,Ⅱ,Ⅲ接受區一樣,但拒收區增加,即繼續檢驗區減小;水平Ⅳ接收區減小,拒收區增加。這樣從檢驗水平Ⅰ→Ⅳ,檢驗水平逐步加嚴。 圖2 檢驗區示意圖 與表4中α,β對應的門限系數μα,μβ見表5。從圖2及表5看出,如果取α=0.3,β=0.7,即兩條檢驗判定線重合,說明檢驗嚴,要么合格,要么不合格,中間沒有繼續檢驗區。 表5 與α,β對應的門限系數μα,μβ值 表中給出了一個i=0的點,在判斷格式里為t10點,即無失效門限t10,r=0時的接受門限值,該點尤其適用于軍品軸承試驗套數少,而又要求無失效試驗的特點。 2.3.4 檢驗判定格式 表6 檢驗判定格式 2.3.5 檢驗判定式 若0≤i<5,Ti>t1i為合格(接受);Ti 若i=5,t15-T5≤T5-t25為合格;否則為不合格。 2.3.6 可靠度Re 2.3.7 序貫試驗實例 圓錐滾子軸承質量要求:L10t/L10h≥Z′為合格,Z′為1.2。 計算t1i及t2i,其檢驗判定格式見表7。 表7 檢驗判定表 情況1:當試至200 h,尚無失效軸承出現,這時12套軸承均試至200 h。 判定該批軸承樣品合格。 (100+180]1.5/121.5=2801.5=4 685,t22 3 336 當試至455 h,第3套軸承失效,L3=455 h,T3=4551.5=9 705>t13=9 612,合格停試。 判定該批軸承樣品合格。 情況3:當L1=180 h,T1=1801.5=2 414,t21 當L2=220 h,T2=2201.5=3 263,T2 判定該批軸承樣品不合格。 情況4:如果是長壽命試驗時,還應給出達到合格倍數的值(K值),即達到Z′的倍數值;相應的可靠度Re等。 若12套軸承試至500 h均無失效,則: 設K=3,則t10=8 418,合格;K=4,則t10=11 225,不合格。 假設某軸承L10h=100 h,N=12套和N=8套,b=1.5,在不同質量系數、不同檢驗水平風險時的最小無失效時間比較見表8。 表8 最小無失效時間比較 由于序貫試驗風險較大,所以判定加嚴。 N=12套時,球軸承Z′=1.4,檢驗水平α=0.2,β=0.3,最小無失效時間約比L10h增大50%;滾子軸承Z′=1.2,檢驗水平α=0.2,β=0.3,最小無失效時間約比L10h增大30%。 對圖估計、參數估計,球軸承L10t/L10h≥1.4為合格,即超過L10h的40%為合格;滾子軸承L10t/L10h≥1.2為合格,即超過L10h的20%為合格。 由于序貫試驗風險較大,相比較其判定均比圖估計、參數估計加嚴一定的比例。故3種數據處理結果基本一致。 N=12套時,球軸承Z′=1.4,檢驗水平α=0.2,β=0.3,最小無失效時間為148 h;Z′=1.05,檢驗水平α=0.3,β=0.3,最小無失效時間為100 h,兩者相差約50%。 滾子軸承Z′=1.2,檢驗水平α=0.2,β=0.3,最小無失效時間為133 h;Z′=1,檢驗水平α=0.3,β=0.3,最小無失效時間為97 h,兩者相差約40%。 相同質量系數、檢驗水平下,試驗套數N=8較N=12的試驗時間長約30%,即試驗套數減少,試驗風險將增加。 對于軸承壽命與可靠性試驗,如果失效數據不少于6個,試驗評定采用Weibull分布圖估計、參數估計,可以給出試驗評定結果;對于小子樣失效數據、無失效數據的處理則采用序貫試驗,較短時間就能得出評定結果,可以大大提高試驗的效率。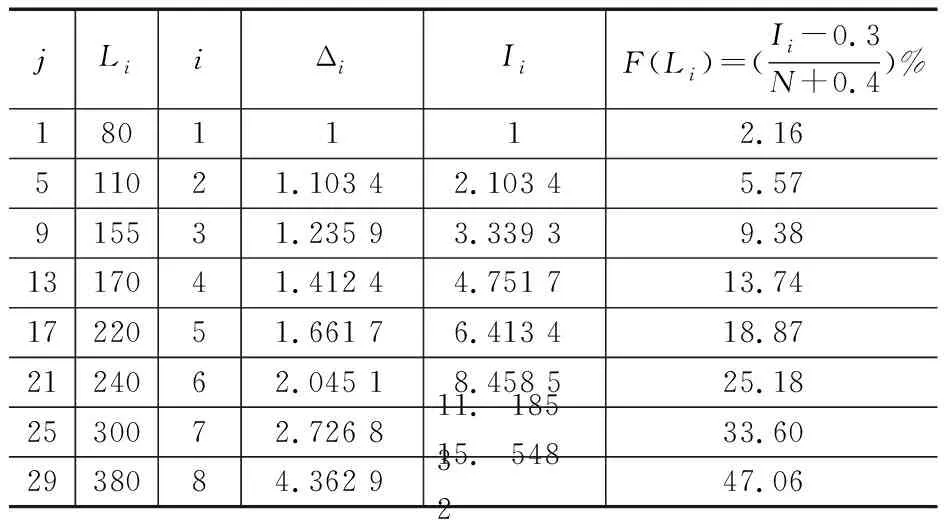
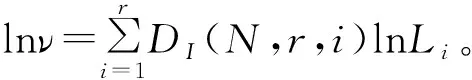

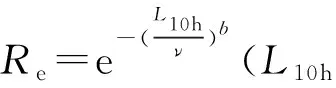
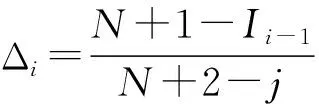
2.3 序貫試驗方法
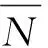

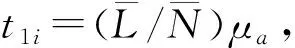
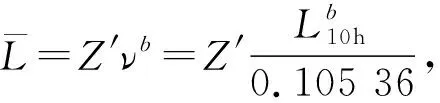

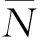
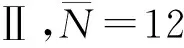
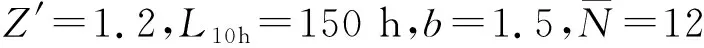

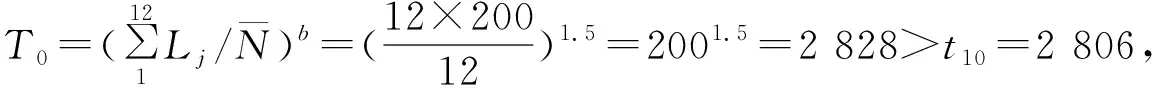
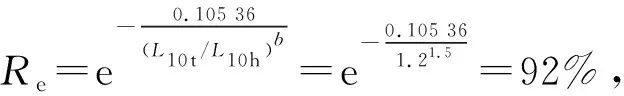
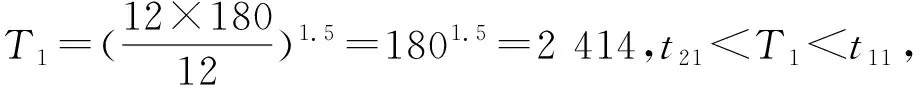
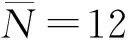
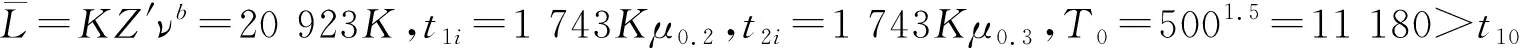
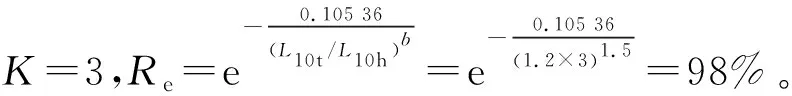
3 試驗驗證
3.1 序貫試驗與圖估計、參數估計比較
3.2 不同質量系數、不同檢驗水平比較
3.3 不同試驗套數比較
4 結束語

