基于遺傳算法的無源濾波器參數的優化
丁龍祥
(江蘇海事職業技術學院,南京 211170 )
1 引言
無源濾波器是靜止型無功補償器的重要組成部分[5],它主要作用是濾除電網諧波及補償無功。本文以單調諧濾波器和高通濾波器作為參數調節的研究對象。
傳統的遺傳算法一般用來解決單目標、無約束的問題。缺點有:基本遺傳算法在解空間進行隨機搜索尋找最優解,而非確定性的迭代求解,遺傳和變異的完全隨機性雖保證了進化的搜索功能,但也使得一些好的優良個體被過早破壞。從過程來看,其初始解的產生、繁殖、變異都是隨機完成的。遺傳算法依靠產生大量的個體進行適者生存選擇而逐步逼近最優解,這種完全隨機化的過程雖然可以在整體上保證了進化,但卻是一個漫長、隨機的過程,計算效率低。另外遺傳算法的選擇算子、雜交算子的尋優功能隨進化迭代次數的增加而逐漸減弱,在應用中常出現早熟收斂現象。當某一局部最優解和全局最優解較為接近時,個體之間的差別不大,多樣性減少,搜索區域不斷減少而導致結果落入局部最優。因此,要解決無源濾波器的多目標優化設計問題,在算法上必須作一定的改進。
2 遺傳算法的改進
作為遺傳算法重要的遺傳參數的交叉概率 Pc和變異概率Pm。其最佳取值隨具體應用、種群分布和遺傳進化而變化;Pc、Pm取值固定是 SGA易早熟收斂和搜索效率較低的重要原因,這里引入自適應交叉概率和變異概率可較好地解決該問題。
用不同的方法對自適應遺傳算法做改進,它既考慮解的全局性又考慮解的收斂性,取值如下:
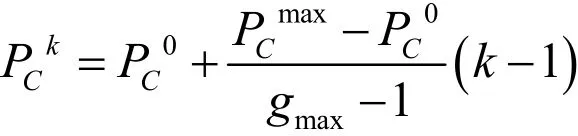
式中 k為迭代次數;為交叉概率的初值;為交叉概率末值;gmax為最大允許的迭代次數。這樣交叉概率就會隨迭代次數增加而減小,從而避免上述問題。但是沒有考慮到概率的變化同適應度函數的關系。而適應度函數值才是衡量性能指標的重要參數。
為此,本文對上述自適應遺傳算法加以改進,
具體如下:
式中: fmax—代表群體中最大的適應度值
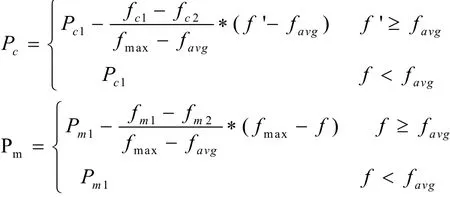
favg—每代群體的平均適應度值;f/—要交叉的兩個個體中較大的適應度值;f—要變異個體的適應度值。
其 中 PC1=0.9,PC2=0.6,Pm1= 0.1,Pm2=0.001
在改進的自適應遺傳算法中,相應地提高了群體中表現優良的個體的交叉率和變異率,使得它們不會處于一種近似停滯不變的狀態。為了保證每一代中的優良個體不被破壞,采用最優個體保存方法,使它們直接復制到下一代中。
3 無源濾波器設計原則和方案
3.1 無源濾波器設計原則
在實際應用中,一般是根據電網的諧波狀況來確定無源濾波器的類型和組數[2],如諧波源為帶阻感負載的三相全控整流橋[4],其特征諧波為6k±1(k為自然數)次,則應裝設5,7次單調諧濾波器和二階高通濾波器各一組。無源濾波器參數的設計應遵循以下原則:
(1)電容、電感、電阻之間的關系滿足系統無源濾波器的濾波原理;
(2)無源濾波器的整體基波等效阻抗滿足系統無功補償的要求;
(3)無源濾波器的整體阻抗不應與電網阻抗形成串、并聯諧振;
(4)裝設無源濾波器后的電網諧波含量低于國家標準;
(5)各組無源濾波器諧波容量的計算不僅要包含各自所濾除的諧波容量,還要加上10%的背景諧波容量。
3.2 優化問題方案
在以上原則的基礎上,進行無源濾波器參數的優化設計[1],還必須考慮三個問題。
(1)裝設無源濾波器的初期投資最小;
(2)無源濾波器的裝設既不能使系統出現無功功率過補償現象又要使系統的功率因數盡量接近1;
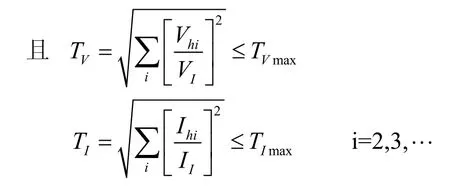
(3)無源濾波器的裝設要使電網諧波含量在低于國家標準的基礎上,越低越好。為了分析的方便與統一,諧波電壓、電流含量均以總畸變為衡量標準,即TV和TI式中Tv、T1分別為電壓、電流的總畸變率;V1,I1為基波電壓和電流;Vh1,Ih1為第i次諧波電壓和電流;Tvmax,I1max分別為電壓、電流總畸變的上限一般根據國家標準計算。
因此,無源濾波器參數的優化設計問題,就是要滿足上述約束條件,這里采用一種改進的混沌遺傳算法來解決這個多目標優化問題。
4 具體計算實例
某軋鋼廠母線的主要諧波源是4臺整流變壓器[4],實測電網諧波電流如表1 所示,因此特征諧波的次數為5,7,11次。系統的平均功率因數cosφ1為 0.75,設計后的平均功率因數 cosφ2為0.92。因此,所需無功功率可由式計算 :
Q = P(tanφ2--tanφ1)
配電網在裝設濾波器組前,各次主要諧波電流如表所示。由表 1中可知5次,7次。11次諧波電流值較大,其中5次諧波電流嚴重超標。由表2的各次諧波電流允許值及綜合考慮應該補償的無功功率和各次諧波含有率,決定在配電網中裝設5次,7次,11次單調諧濾波器和高次濾波器。
為使濾波器滿足諧波指標和無功補償的要求,用上述方法對濾波器進行優化,以裝設一組高通濾波器。在單調諧濾波器設計中,LC參數的選擇會影響濾波效果,特別是當電網頻率或LC參數發生漂移時的濾波效果,因此需要選擇最佳的品質因數Q,以保證濾波器對頻率的選擇性和濾波器在頻漂及參數漂移下的濾波效果。在高通濾波器設計中,各參數的恰當配合,可大大改善濾波器效果并減小其有功損耗。在此引入了一個與品質因數相關的參數m,其中m=L/R2C,通過品質因數Q和m,可以建立濾波器中的電感,電容及電阻的關系。因此,選擇各濾波支路的電容量C5C7C11優化的獨立變量。對于兼作無功補償的濾波器,應使濾波器組補償的無功總量與系統的要求一致,對優化設計的結果采用了性能評價,即在配電網中加裝無源濾波器組后,電網總諧波電壓畸變率最小為優化目標[3]。

表1 濾波前測得各次主要諧波電流
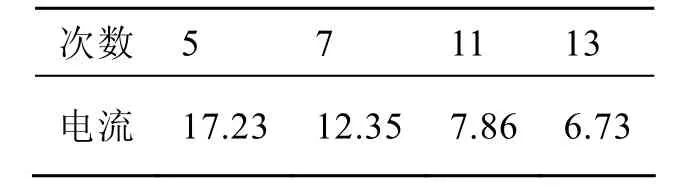
表2 各次諧波電流允許值
1) 染色體編碼
染色體代表解的形式,包含所有的遺傳信息,本文根據無源濾波器設計原則來構成染色體的基因鏈,采用實數制編碼,對于單調諧濾波器有
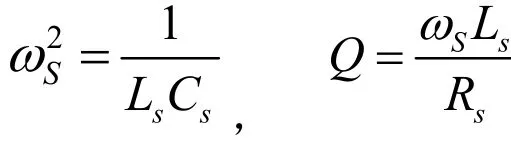
這里以二階高通濾波器為例,有
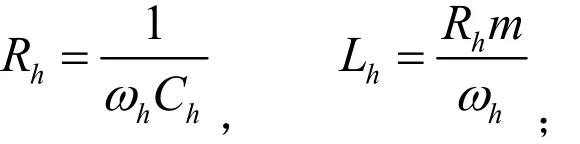
式中ωs,Ls,Cs, Rs和Q分別為單調諧濾波器的諧振頻率、電感值、電容值、電阻值和調諧銳度;ωh,Lh,Ch, Rh,m分別為二階高通濾波器所對應的截止頻率、電感、電容、電阻和調諧值。ωs,ωh是由諧波源的特征諧波確定的常數,所以每組無源濾波器的各個參數均可由電阻和電感兩個參數來表示,因此,染色體可表示為一個2n維的基因鏈。
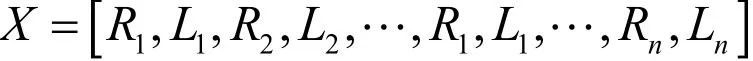
式中,n為無源濾波器的組數(這里5次、7次、11次濾波器和高通濾波器)。
2) 適應度函數
根據優化目標,構造如下適應度函數:
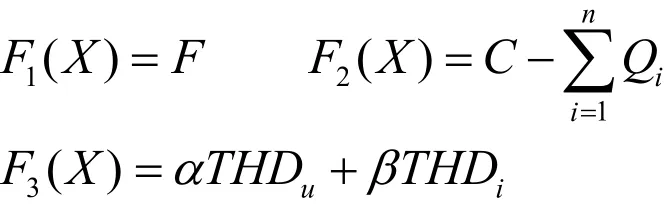
式中 C是一個較大的正數,用來保證F2(X)為正值,其值可以根據實際情況確定;α和β大于零的常數,用來匹配電壓、電流畸變率的權重,一般α:β=1:10。
3) 結果
各參數結果如表3 所示,表4為安裝濾波器后測得的各次主要諧波電流。對比表1和表2發現各主要次諧波畸變(5次、7次、11次等)在裝設濾波器后都有了明顯改善,同時由實測可知配電網的功率因數在系統滿載時也保持在 0.9以上。以上結果說明把遺傳算法應用于濾波器的設計不僅可以得到令人滿意的結果,同時還大大減小了人工的計算量,而且明顯提高了算法的尋優速度。
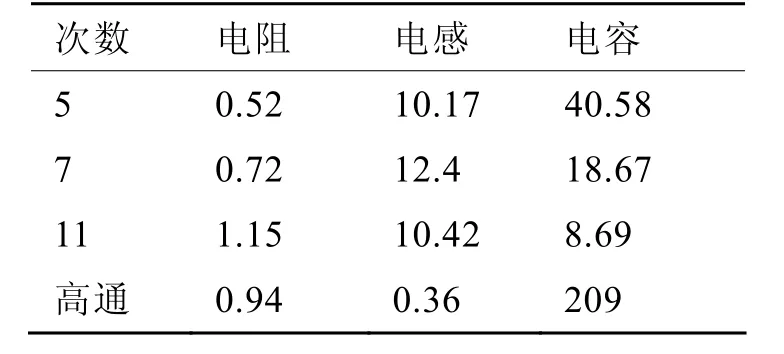
表3 優化后濾波器參數

表4 濾波后測得各次主要諧波電流
由以上可知,無源濾波器的設計是一個多約束、非線性的多目標優化問題。應用改進遺傳算法對濾波器LC參數進行優化,兼顧諧波抑制和無功補償的要求。該方法假設條件少,尋優空間大、尋優速度快。對實際工程的求解表明,把改進遺傳算法應用于無源濾波器的設計過程中是非常有效的。
:
[1]崔國瑋, 李志民. TCR動態無功補償原理及濾波器參數的計算.包頭鋼鐵學院學報, 2002,17:284-288.
[2]吳競昌等. 供電系統諧波. 北京: 中國電力出版社,1998.
[3]翁利明. 抑制電力系統高次諧波的有效方法. 電力電容器, 1998 ,(4):1-6.
[4]翁利民, 陳允平, 智萍. 電弧爐的電壓閃變與抑制.工業加熱, 2001, 6:26-28.
[5]王兆安等. 諧波抑制和無功功率補償. 北京: 機械工業出版社, 1998.

