擴展整數帳篷映射與動態散列函數

劉建東

(北京石油化工學院 信息工程學院，北京 102617)

1 引言

散列函數在現代密碼學中有著極其重要的用途，它不僅在安全通信中起著重要的作用，而且是許多密碼算法與密碼協議安全的前提條件。近幾年來，密碼學界對散列函數的設計與分析給予了廣泛的關注。在 2004年美密會上，王小云等宣布了包括MD4、MD5、HAVAL-128以及RIPEMD在內的碰撞實例[1]。最為重要的是對MD5的破解不僅具有理論意義，而且在實際應用領域也產生了巨大的影響。Lucks與Magnus已構造出MD5的“有意義的碰撞”[2]。王小云等人對SHA-1的分析也已取得突破性成果，揭示出SHA-1的脆弱性[3]。

傳統的散列函數(MDx系和SHA系)的主要設計原則基于MD迭代結構[4]，它們具有許多共同的設計準則，各輪的混合運算設計極為相似，全都采用了整數模加和邏輯函數(輪函數)。如此眾多的散列算法在不長的時間相繼被攻破，說明其設計準則存在缺陷。近年來，為獲得更安全的散列函數，利用混沌系統對變量和參數的變化的敏感特性構造單向散列函數的研究已取得一些進展[5～9]。但由于數字化混沌系統的動力學特性退化問題[10]及構造方案本身的缺陷[11]，目前基于混沌理論的散列函數構造方案還無法得到人們的信任。文獻[12]中首次將混沌散列函數的研究成果[13,14]與傳統的散列函數設計準則相結合，設計了一種輸出長度為160bit的散列函數。本文對文獻[12]提出的整數帳篷映射進行了改進，給出擴展整數帳篷映射的定義，并對擴展整數帳篷映射的均勻分布特性進行了分析。在此基礎上,本文給出一種基于擴展整數帳篷映射的具有動態特性的散列函數設計方案(簡稱 TDHA)。該方案各輪主要計算過程依然是整數模加和位運算，為了提供良好的擴散性，將擴展整數帳篷映射作為各輪的主要非線性部件，由擴展整數帳篷映射引發狀態變量內部及狀態變量之間的動態強差分擴散。該方案將傳統的散列函數中所使用的常數變為動態參數，利用擴展整數帳篷映射的位邏輯判定功能，通過循環移位方式控制動態參數的演化過程，增強了參數項與明文差分的關聯度。壓縮函數內部采用了并行迭代結構，有利于算法的軟硬件高速并行實現。另外，還對MD結構進行了改進，使得壓縮函數之間不僅有狀態變量鏈接，還有相同數量的動態鏈接參數，在無需擴展中間狀態變量的情況下，提高了散列函數抵抗部分消息碰撞攻擊的能力。

2 基于整數帳篷映射的耦合映像系統

2.1 整數帳篷映射

帳篷映射的定義為[6]

該映射是混沌的。當參數α=0.5時，帳篷映射為滿映射。帳篷映射的優異特性之一是其具有均勻的分布函數，在實數域內其性態是混沌的。將其由實數域運算等價轉化為整數運算(設整數的二進制位數為k)：

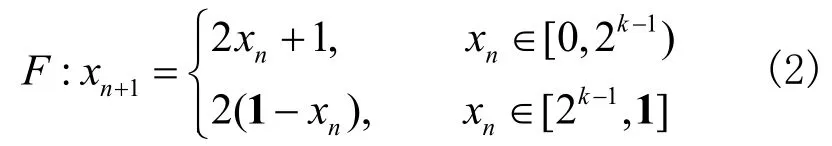
其中 1＝2k-1。式(2)中的乘法運算可用移位操作實現。映射F服從[0, 1]上的均勻分布。更為重要的是，整數帳篷映射保持了實數域帳篷映射的伸長和折疊特性，其伸長特性最終導致相鄰點的指數分離，即敏感的初始條件，其折疊特性則保持生成序列有界，且引起映射不可逆。然而，由于映射(2)定義在有限域內，利用它生成的迭代序列必然進入周期態，甚至出現一些周期長度很小的周期點。例如k=4時，出現不動點(10→10→…)；k=5時，出現周期長度為2的短周期(12→25→12→…)。

2.2 擴展整數帳篷映射

為了改進整數帳篷映射的性態，給出擴展整數帳篷映射,將其定義為

當n為偶數時，

當n為奇數時，

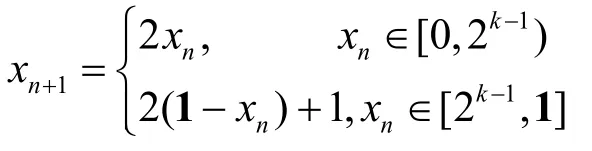
映射式(3)將生成的迭代序列的周期擴展到2(k+1),并且避免了不動點的出現。表1給出k=5時，從所有可能的初值出發，利用映射式(3)生成的迭代序列，其周期為12。從表中可以明顯看出其均勻分布的特性及拉伸與折疊的非線性特征。

表1 擴展整數帳篷映像（k=5）

2.3 擴展整數耦合帳篷映像系統

分析表1中的數據發現，映射式(3)生成的迭代序列共包含6個周期環，這些周期環是：

0→1→2→5→10→21→21→20→23→16→31→0→0,6→13→26→10→20→22→19→24→15→31→1→3→6,3→7→14→29→5→11→22→18→27→8→16→30→3,17→28→7→15→30→2→4→9→18→26→11→23→17,8→17→29→4→8,9→19→25→12→24→14→28→6→12→25→13→27→9。

在迭代過程中，通過施加擾動，來打破擴展整數帳篷映射所固有的周期環，則可以改善整數帳篷映射的遍歷性，使系統的迭代序列隨機化。為此，構造如下的耦合映像系統模型：

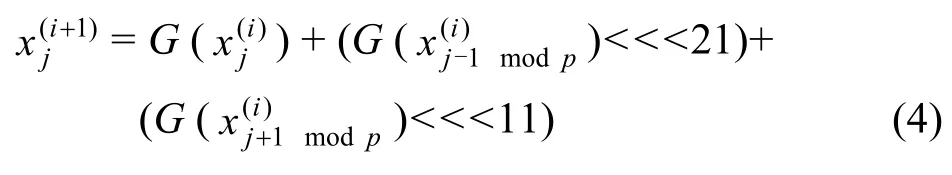
式(4)中運算符含義見下文中的說明。該式采用耦合映像格子的并行迭代結構及傳統散列函數中的模加耦合方式，繼承了耦合映像格子模型的混淆與擴散特性，克服了耦合映像格子模型對格點序列分布特性的影響[14]。取p=5, j=0,…,4，圖1為式(4)在隨機選取一組初值時狀態變量經12 000次迭代的結果，可看出時間序列具有均勻隨機的特性。

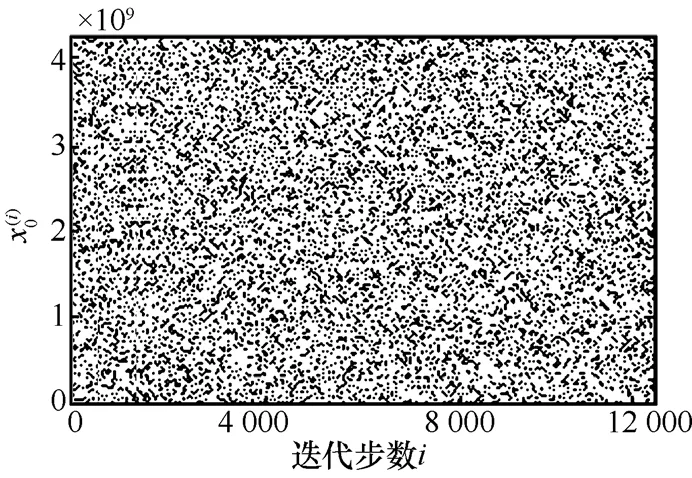
圖1 擴展整數耦合帳篷映射時間序列分布

3 TDHA構造

符號說明：+為mod 232的加法運算，～為逐比特邏輯反，⊕為逐比特邏輯異或，＜＜為左移位操作，＜＜＜為循環左移位操作，＞＞＞為循環右移位操作。

定義D=231，在GF(232)內，擴展整數帳篷映射(式(3))G:xn→xn+1可用 C語言中的三元運算符(? :)描述為：

當n為偶數時，

xn+1= xn＜D ? (xn＜＜1)+1 : ～xn＜＜1；

當n為奇數時，

xn+1= xn＜D ? xn＜＜1 : (～xn＜＜1)+1。

由此可見，擴展整數帳篷映射可用簡單的邏輯判斷、邏輯取反及移位操作實現。若用匯編語言或硬件實現，則其操作可以進一步簡化為：當n為偶數時，測試字的最高位是否為0，若為0,則左移一位加1，否則，則各位求反后，左移一位；當n為奇數時，測試字的最高位是否為 0，若為 0，則左移一位,否則，則各位求反后，左移一位，再加1。編程實現時，n的奇偶性無需判定，只要在一次循環中包含2次映射即可(奇偶各一次)。在下面的散列算法設計中，擴展整數帳篷映射的邏輯判定結果還將引起參數項k的動態變化，將其統一用三元運算符（? :）描述。下面給出構造散列算法TDHA的一般過程。

1) 分割與填充。采用MD5算法的分割與填充方式。簡要描述為:將任意長度的明文消息 M 分割成 512bit的消息塊 M0,…,Mn,…,Mt，最后一個塊填充為:Mt=*…*10…0Length(M),其中 Length(M)表示M的長度的二進制形式，長度為64bit，不足64bit時高位添一個介符1再補0。

2) 將每個消息塊Mn劃分成16個32bit的消息字 m0, m1,…,m15。

3) 5個32bit的初始向量：

5) TDHA算法：

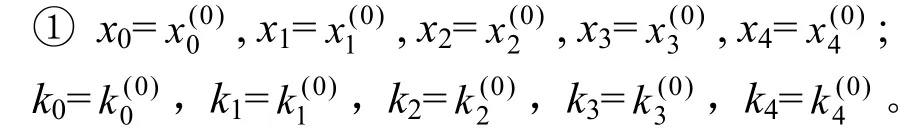
② 作3輪計算，每一輪進行4次迭代操作,每次迭代操作需要先進行消息嵌入及映射變換，然后利用式(4)給出的耦合映像系統模型，進行擴散迭代。

第1輪：進行4次迭代操作。

迭代操作1：

xi= mi+ xi, i=0,…,3。

x4= (m0⊕m1⊕m2⊕m3)+x4。

Gi= xi＜D?(xi＜＜1)+1:(ki+2mod5=ki+2mod5＞＞＞1,～xi＜＜1), i=0,…,4。

xi=Gi+((Gi-1mod5⊕Gi+2mod5)＜＜＜21)+

((Gi+1mod5⊕Gi+3mod5)＜＜＜11)+ ki, i=0,…,4。

迭代操作2：

xi= mi+4+ xi, i=0,…,3。

x4= (m4⊕m5⊕m6⊕m7)+x4。

Gi= xi＜D ? xi＜＜1:(ki+2mod5=ki+2mod5＞＞＞1, (～xi＜＜1)+1), i=0, …,4。

xi= Gi+ ((Gi-1mod5⊕Gi+2mod5)＜＜＜21)+((Gi+1mod5⊕Gi+3mod5)＜＜＜11)+ ki, i=0,…,4。

迭代操作 3：

xi= mi+8+ xi,i=0,…,3。

x4=(m8⊕m9⊕m10⊕m11)+x4。

Gi= xi＜D?(xi＜＜1)+1:(ki+2mod5=ki+2mod5＞＞＞1,～xi＜＜1), i=0,…,4。

xi= Gi+ ((Gi-1mod5⊕Gi+2mod5)＜＜＜21)+((Gi+1mod5⊕Gi+3mod5)＜＜＜11)+ ki, i=0,…,4。

迭代操作4：

xi= mi+12+ xi,i=0,…,3。

x4=(m12⊕m13⊕m14⊕m15)+x4。

Gi= xi＜D ? xi＜＜1 : (ki+2mod5=ki+2mod5＞＞＞1,(～xi＜＜1)+1) i=0,…,4

xi= Gi+ ((Gi-1mod5⊕Gi+2mod5)＜＜＜21)+((Gi+1mod5⊕Gi+3mod5)＜＜＜11)+ ki, i=0,…,4。

第2輪：映射變換及耦合擴散迭代的方式與第1輪相同，因此，這里只給出4次迭代操作的消息嵌入情況。

迭代操作5：

xi= (m(15-(3i+1mod5)＜＜＜5)+ xi, i=0,…,4。

迭代操作6：

xi= (m(10-(3i+1mod5)＜＜＜5)+ xi, i=0,…,4。

迭代操作7：

xi= (m(5-(3i+1mod5)＜＜＜5)+ xi, i=0,…,4。

迭代操作8：

x0=( m0＜＜＜5)+ x0，

x1=(( m3⊕m15⊕m11⊕m7)＜＜＜5)+x1，

x2=(( m2⊕m14⊕m10⊕m6)＜＜＜5)+x2，

x3=(( m1⊕m13⊕m9⊕m5)＜＜＜5)+x3，

x4=(( m0⊕m12⊕m8⊕m4)＜＜＜5)+x4。

第3輪：消息嵌入情況(映射變換及耦合擴散迭代的方式仍與第1輪相同)。

迭代操作9：

xi= (m(15-i)＜＜＜9)+ xi, i=0,…,3。

x4=(( m3⊕m14⊕m9⊕m4)＜＜＜9)+x4。

迭代操作10：

xi= (m(11-i)＜＜＜9)+ xi, i=0,…,3。

x4=(( m2⊕m13⊕m8⊕m7)＜＜＜9)+x4。

迭代操作11：

xi= (m(7-i)＜＜＜9)+ xi, i=0,…,3，

x4=(( m0⊕m15⊕m10⊕m5)＜＜＜9)+x4。

迭代操作12：

xi= (m(3-i)＜＜＜9)+ xi, i=0,…,3。

x4=(( m1⊕m12⊕m11⊕m6)＜＜＜9)+x4。

④ 對剩下的消息塊繼續②～③的操作，直到最后一塊。

⑤ 最后輸出160bit的散列值：x0|| x1|| x2|| x3||x4。

上述算法有以下特點。

1) 用擴展整數帳篷映射取代傳統的邏輯函數。傳統的散列函數在混合運算中采用了邏輯函數(輪函數)。以MD5為例，在壓縮函數的設計中，為了實現消息的擴散與混淆，主要采用了4個基本邏輯函數。在這些邏輯函數中，多個不同的輸入會產生相同的輸出，稱之為邏輯函數的值碰撞。以f1=f(A,B,C)=(A∧B)∨(∧C)為例，輸入為(0,0,0)、(0,1,0)、(1,0,0)、(1,0,1)時，輸出為 0；輸入為(0,0,1)、(0,1,1)、(1,1,0)、(1,1,1)時，輸出為1。由于邏輯函數的值碰撞，使壓縮函數內部可能產生差分收斂性。王小云等正是利用邏輯函數的這一特性來控制差分的收斂，并結合整數模減差值表達式多樣性、左循環移位差值傳遞特性及比特修改與 2-block碰撞攻擊技術找到了MD5算法的碰撞實例。

擴展整數帳篷映射具有均勻分布性及良好的非線性特征，并且實現簡單，運算速度快，但它是單變量間的1-1映射，不存在值碰撞問題。另外，傳統的散列函數中，消息是不能注入邏輯函數的，否則，在邏輯函數中即可產生消息碰撞。而在TDHA算法中，帳篷映射不會導致消息碰撞，因而消息可直接注入擴展整數帳篷映射中，即消息注入時就進行了非線性變換，增強了算法的不可逆性。

2) 擴展整數帳篷映射引發動態強差分擴散。傳統的散列函數(MD5、SHA-1等)的擴散機制是由模32加和按位進行的布爾操作的混合運算實現的，每一比特的變化只有通過移位或進位操作來影響其他的位。TDHA算法仍具有邏輯移位及模32加的擴散機制，尤為重要的是，每一次映射變換除了能使狀態變量左移一位之外，最高比特位的差分特性還將引發該狀態變量產生最大的擴展碼字重量，稱這種現象為狀態變量內部的動態強差分擴散。在 3輪操作中，通過循環移位及耦合擴散，每一消息比特差分均有機會觸發動態強差分擴散。此外，TDHA算法用動態參數項取代了傳統散列函數中所使用的常數，消息差分可以引發動態參數項產生不同的演化過程，這一過程發生在不同的狀態變量之間，因而我們稱之為狀態變量間的動態強差分擴散。

對壓縮函數的內部結構進行密碼分析,目前最有效的方法是王小云等提出的模減差分分析方法。該方法構造有效的差分路線的主要思想是去抵消由于消息差分引起的擴散。差分攻擊的復雜度與壓縮函數中消息的差分擴散程度成正比，因此差分擴散程度越大，構造的碰撞差分路線的導出條件就越多。TDHA算法引入動態強差分擴散機制，加速了差分擴展，使只修改少數幾位就能產生一個碰撞的概率變得更小，對“差分路線”形成一道難以逾越的屏障。

3) 關于動態參數項的說明。在傳統散列函數中，一般均含有固定的常數項。以 MD5為例，除了4個初始狀態(A,B,C,D)外，另外還有64個常數Ti(Ti=232abs(sin(i),1≤i≤64)，在MD5算法的64步混合操作中，每步依次使用一個常數，因此，每步操作使用的常數是固定不變的。文獻[15]提出變參數概念，并對 MD5算法進行了改進。方法是：構造一個參數表T(T[0], …,T[256])，利用消息序列的前68個字節(不足時補0)生成一個68字節的索引序列I(I[0], …,I[67])，在索引序列I與參數表T之間利用一個映射，實現參數的動態提取。該方法將MD5算法中的靜態常數項變成了動態參數。但該算法存在以下幾個問題：① 變參僅由消息序列的前68個字節決定，也就是說，對68個字節以后的消息差分而言，并不引起參數項的變化；② 攻擊者可以從參數表T中先選定一組自己所期望的參數，然后根據映射關系逆推消息序列的前 68個字節，這樣，對攻擊者而言，又轉化為對固定常數項的MD5算法的攻擊；③ 為了實現參數可變，需要一個擴展的參數表，新定義一個標志數組，還需要生成一個索引序列，因而資源消耗較多。

設計散列函數的一個基本準則是明文消息每比特的變化均能引起散列值中近 50%比特發生改變。因此，如果使參數項的取值與明文消息每比特的變化均相關，無疑對提高散列函數的安全性是極為有利的。TDHA算法只選定5個初始參數，利用擴展整數帳篷映射的位邏輯判定功能，通過循環移位方式控制動態參數的演化過程，增強了參數項與明文差分的關聯度，而編程實現又極為簡單。表 2給出迭代過程中，參數的動態演化過程。限于篇幅，表中只列出部分動態參數值。從表2中的數據可看出，明文消息改變一個比特，就會引起動態參數的演化過程發生很大變化。

4) 對MD結構的改進。基于MD結構的散列函數一般形式如圖2所示。

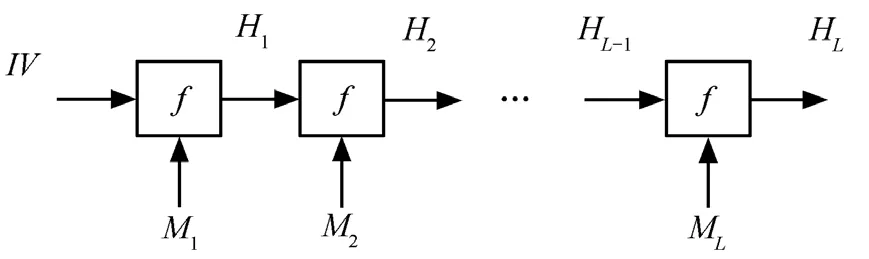
圖2 基于MD結構的散列函數

基于MD結構的散列函數具有簡單、高效和支持流處理技術等特點。但近年的研究發現，基于MD結構來構造散列函數存在嚴重的安全缺陷。由于MD結構的散列函數采取迭代級聯方式，只要出現了碰撞而且余下的輸入一樣，那么散列值就一定相同，若消息 m和m′有相同的散列值，則對任意的X，有h(m||X)=h(m′||X)。針對這一安全隱患，甚至可以構造出具有實際意義的碰撞實例。為了解決這種部分消息碰撞問題，文獻[16]提出采用并行層疊方式來擴展中間狀態。但這種改進方式是以降低執行效率為代價的。本文提出的TDHA算法，除了有5個32bit的字組成的160bit的中間狀態變量，另外還有 5個動態演化參數，前級的輸出狀態H(160bit)及動態參數演化結果K分別作為后級的初始向量及動態參數的初始值(如圖3所示)，若消息m和m′有相同的散列值，但動態參數演化結果K和K′不同，則對任意的X，顯然h(m||X)與h(m′||X)不會發生碰撞，只有消息 m和m′有相同的散列值，且動態參數演化結果 K和K′也相同的情況下，對任意的 X，才會有 h(m||X)=h(m′||X)。顯然，由于引入動態參數,在無需擴展中間狀態的情況下，提高了散列函數抵抗部分消息碰撞攻擊的能力。

表2 動態參數的演化過程

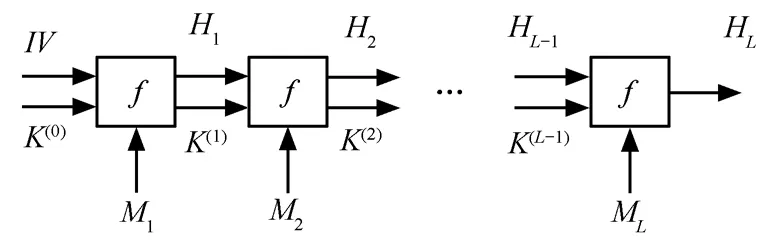
圖3 TDHA的迭代結構

5) TDHA算法秉承了傳統散列算法描述簡單，易于實現的設計理念，借鑒并改進了混沌密碼學研究中廣泛采用的帳篷映射模型，將其從實數域變換到整數域中，利用其拉伸與折疊的非線性本質及均勻分布特性實現消息的混淆與擴散。算法全部采用基于 32bit操作數的一些簡單位操作，便于軟硬件高速實現。

6) 傳統散列函數的操作步只能用串行方式實現，TDHA算法的壓縮函數內部的迭代結構與MD5、SHA-1等不同，適應于并行方式實現。

4 非線性擴散特性的統計分析

密碼算法的混淆與擴散程度可以通過非線性擴散特性的統計檢測給出一個概率上的結論。用統計方法對密碼算法的非線性擴散程度進行分析通常要包括算法的完全性、雪崩效應及嚴格雪崩準則等方面。按文獻[17]的定義：完全性是指函數輸出值的每一個比特都與消息輸入的所有比特有關，雪崩效應是指消息輸入中任意一個比特的改變都應造成輸出平均半數比特的改變，嚴格雪崩準則是指消息輸入中任意一個比特的改變都會造成輸出的每一個比特以1/2的概率發生改變。

設H是一個n bit輸入、m bit輸出的散列算法，輸入向量為x=(x1,…,xn)∈(0,1)n，僅改變x的第i bit后的輸入向量為x(i)∈(0,1)n。它們經過壓縮映射后對應的輸出向量分別記為 H(x)、H(x(i))∈(0,1)m。

(·)j表示向量的第 j bit，w(·)表示向量的漢明重量，#{·}表示集合的勢。設X為散列算法輸入的樣本空間，記 aij=#{x∈X| (H(x))j≠(H(x(i)))j}(其中i=1,2, …,n; j=1,2, …,m)表示X中的輸入向量x和x(i)對應的輸出向量之間第j bit不同的個數；bij=#{x∈X|w(H(x(i))-H(x))=j}(其中 i=1,2,…, n;j=1, 2,…,m)表示X中的輸入向量x和x(i)對應的輸出向量之間的差分漢明重量為j的個數。定義3個統計度量：

完備性程度的度量：

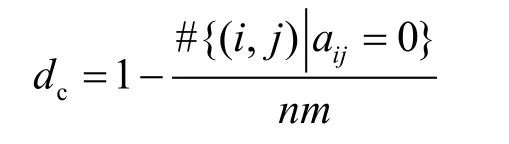
雪崩效應程度的度量：

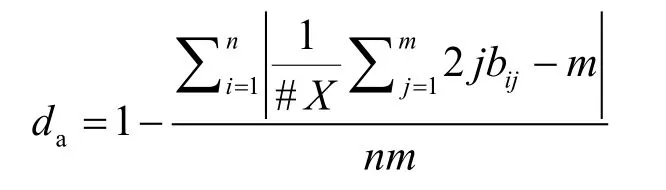
嚴格雪崩程度的度量：

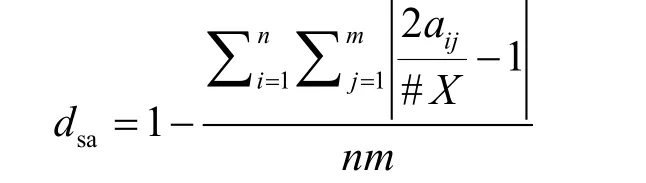
若 H(·)是隨機變換，zα/2表示標準正態分布的α/2分位點，文獻[18]給出如下結論：

1) 測試的樣本量X至少應為nm(zα/2)2；

2) p(dc)=1-2-#X≈1.0；

這里有必要指出：理想的散列函數應該是從所有可能的輸入值到有限可能的輸出值集合的一個隨機映射。嚴格地講，像隨機映射這樣的散列函數是不存在的。因為散列函數是確定性的，而確定性和均勻輸出特性意味著輸出的熵大于其輸入的熵。但根據香農熵理論，一個確定性函數決不可能放大熵。本文的設計目標是使散列函數與隨機映射在概率分布上無法區分。一個實際的散列函數，測試其統計量dc、da、dsa，若落入其置信區間，則說明散列算法滿足非線性擴散的基本要求，即可以認為散列函數具有很好的完全性和雪崩效應，滿足嚴格雪崩準則。

取輸入長度n=512bit，輸出長度m=160bit，在顯著水平α=0.05下，理論上得到如下結果：

1) zα/2=1.92, 選取樣本容量X為320 000；

2) dc=1.000 000；

3) E{da}=0.999 888，其置信區間為(0.999 876,0.999 900)；

4) E{dsa}=0.998 589；其置信區間為(0.998 577,0.998 601 2)。

在上述條件下，隨機選取320 000組512bit字(取自Visual C的Rand())的樣本集X作為TDHA算法的消息輸入，實際的測試結果如表3所示。

從表3可以看出，在顯著水平α=0.05的情況下，TDHA算法在迭代7拍之后統計量dc、da、dsa落入了各自的置信區間，從而滿足了散列算法非線性擴散性的基本要求。需要指出的是，為便于軟硬件高速實現，TDHA算法采取了并行迭代結構。而傳統的散列函數(MD5, SHA-1等)若改用并行結構，則很難滿足擴散性要求。

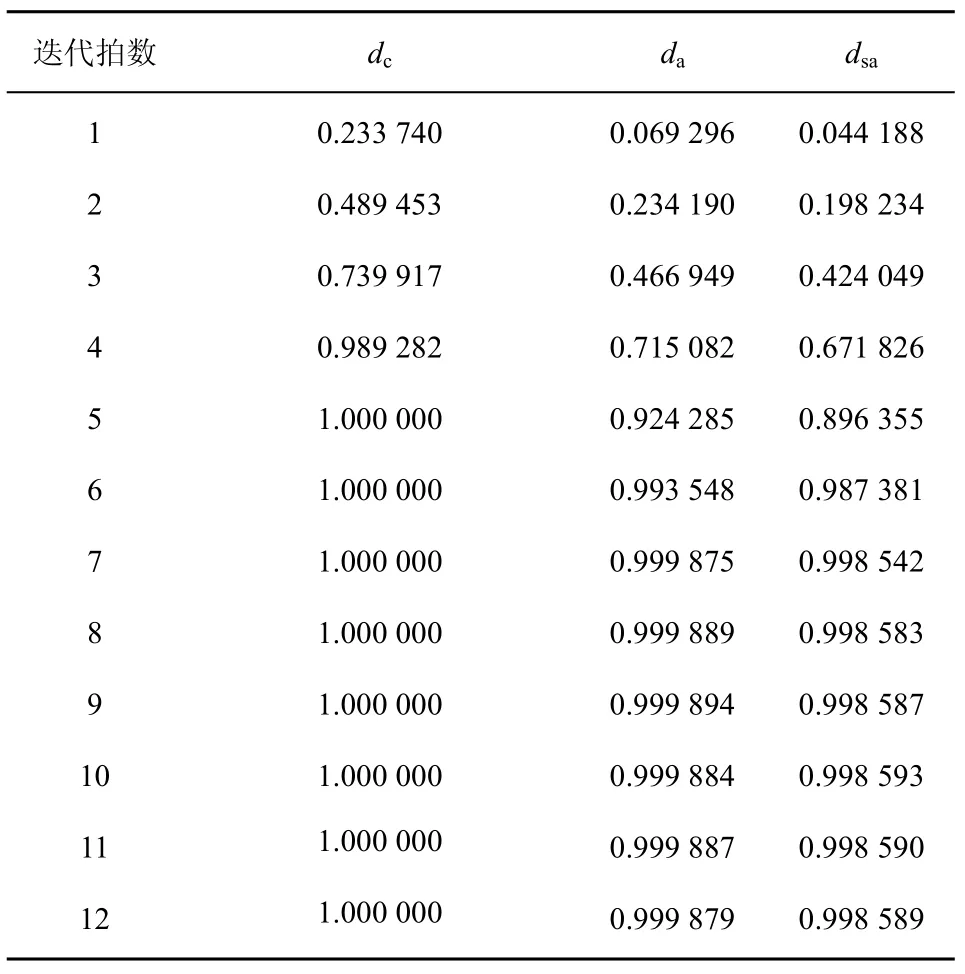
表3 TDHA算法擴散性能的逐拍統計結果

5 抗碰撞性分析

散列函數的值域與定義域相比規模要小得多，是“多對一”映射。找出2個不同的消息，使其產生相同的散列結果稱為碰撞攻擊。通過以下的實驗來定量測試本文算法的抗碰撞能力[9]：在明文空間中隨機選取一段明文求出其散列值，并以單字節字符的方式來表示，然后隨機地選擇并改變明文中1bit的值得到另一新的散列結果。定義2個散列值之間的距離為

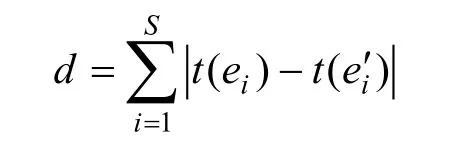
其中，ei和ei′分別是最初的和新的散列值的第 i個字符，S為散列值對應字符的個數，函數 t(·)將 ei和ei′轉換成對應的十進制數。若2個散列值分別由2個獨立的均勻分布的隨機序列所組成，則理論上散列值的單位字符的平均距離為85.33[9]。

取輸入長度n=512bit，隨機選擇輸入樣本，測試其輸出的單位字符的平均距離。經 10萬次統計測試，得到實際的測試結果如表4所示。

從表4可以看出，TDHA算法在迭代7拍之后，其輸出的單位字符的平均距離趨于穩定，并且與理論值十分接近。這一測試結果表明，僅有1bit不同的2個明文所得到的2個散列值統計上由相互獨立的2個均勻隨機序列構成。因此，依據本概率模型，無法將TDHA算法與隨機映射相區分。

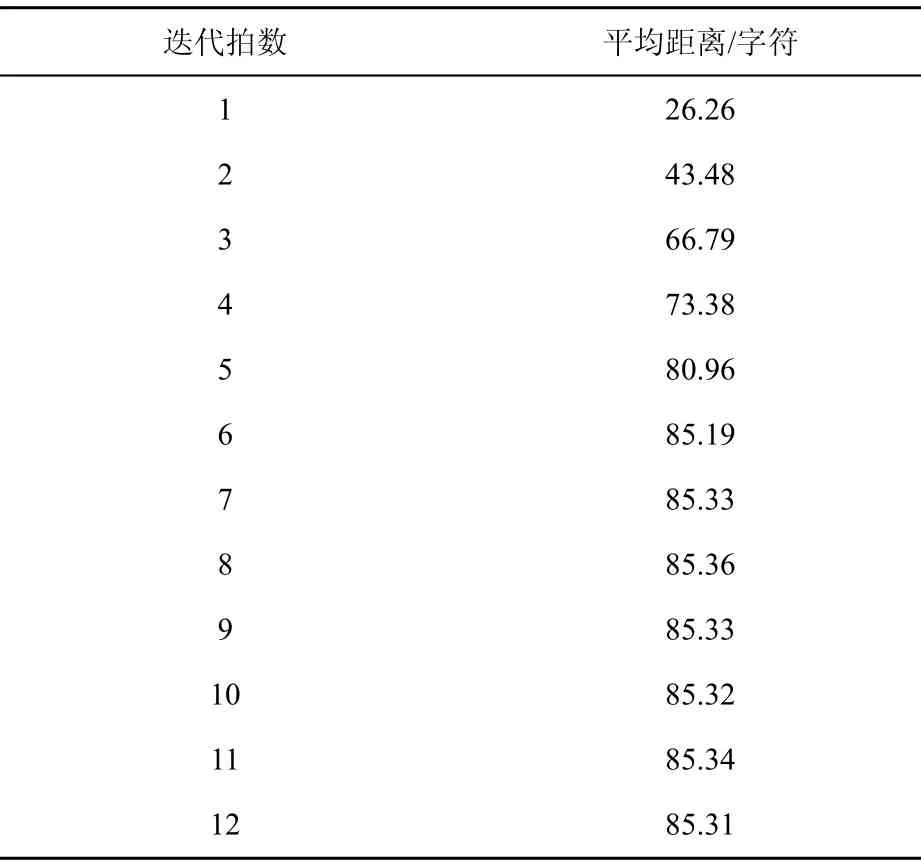
表4 TDHA算法抗碰撞性的逐拍統計結果

6 TDHA算法的速度

TDHA與 SHA-1都輸出 160bit的散列值。SHA-1算法作4輪計算，共計80步混合操作，總共進行224次循環移位，每步混合操作需要進行一次邏輯函數計算；TDHA算法作3輪計算，共計60步混合操作，總共約進行190次循環移位，每步混合操作需要進行一次整數帳篷映射計算。表5給出了在P4、2.0GHz主頻條件下，3種散列函數(TDHA，MD5，SHA-1)用 C語言實現的速度測試結果。從表5可見，TDHA算法已接近MD5算法的速度，比SHA-1算法明顯要快。另外，TDHA算法的內部迭代結構使得它易于并行實現，多處理器環境下，在時間性能上有較大的提升空間。

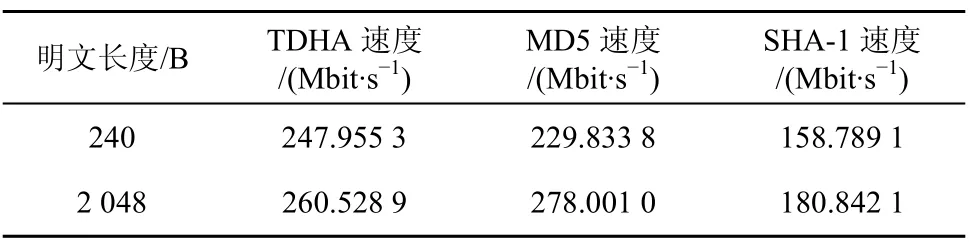
表5 3種散列函數的速度比較

7 結束語

鑒于目前傳統散列函數的安全性受到嚴重威脅，本文主要對散列函數的設計思想進行了一些新的探索，改進了傳統散列函數的設計準則,一方面提高了散列函數的性能，另一方面，也避免了散列算法設計總是走近親路線的現狀。作者希望這些探索能對新的散列函數標準的建立有一定指導意義。

現有的散列函數中，MD5是4輪，SHA-1是4輪，RIPEMD是5輪，HAVAL輪數可變(3到5輪)。本文之所以給出3輪的TDHA算法，除了兼顧算法的執行效率外，同時也考慮到以下因素：人們在進行散列函數的分析與攻擊中，對于多輪的散列函數，總是首先采用降低輪數的辦法來進行。對于大于 3 輪的散列函數，如果降低到 3輪后是不安全的，則該散列函數的安全性也是難以令人信服的，至少可以認為其設計準則存在某些缺陷。

非線性擴散特性分析及抗碰撞性分析結果表明，本文給出的3輪TDHA算法已具有很強的安全性，用統計方法無法將其與真正的隨機函數相區分。TDHA算法實現簡單，并且有明顯的執行效率上的優勢。在今后的改進版本中，將對算法進行優化，通過引入消息擴展機制及增加輪數的辦法，進一步提高算法的安全性。

[1] WANG X Y, FENG D G, LAI X J, et al. Collisions for hash functions MD4, KD5, HAVAL-128 and RIPEMD[A]. Advances in Cryptology－CRYPTO 2004:The 24rd Annual International Cryptology Conference[C]. Berlin:Springer-Verlag, 2004.

[2] LUCKS S, DAUM M. The story of alice and her boss: hash functions and the the blind passenger attack[A]. Rump Session of Eurocrypt’05[C].2005.

[3] WANG X Y, YIN Y L, YU H B. Finding collisions on the Full SHA-1[A]. Advances in Cryptology--Crypto’05[C]. LNCS 3621, 2005.17-36.

[4] DAMGARD I. A design principle for hash functions[A]. Advances in Cryptology:CRYPTO89[C]. volume 435 of Lecture Notes in Computer Science. Springer- Verlag, 1989.416-427．

[5] WONG K W. A combined chaotic cryptographic and hash ing scheme[J]. Phys Lett A, 2003,307:292-298.

[6] YI X. Hash function based on chaotic tent maps[J]. IEEE Transactions on Circuits and Systems-Ⅱ: Express briefs,2005,52(6):354-357

[7] 劉軍寧, 謝杰成, 王普. 基于混沌映射的單向散列函數構造[J]. 清華大學學報, 自然科學版,2000,40(7): 55-58.LIU J N , XIE J C, WANG P .One way hash function construction based on chaotic mappings[J]. Journal of Tsinghua University, Science& Technology, 2000,40(7):55-58.

[8] XIAO D, LIAO X F, DENG S J. One-way hash function construction based on the chaotic map with changeable- parameter[J]. Chaos, Solitons and Fractals,2005,24:65-71.

[9] 盛利元, 李更強, 李志煒. 基于切延遲橢圓反射腔映射系統的單向散列函數構造[J]. 物理學報, 2006,55(11):5700-5706.SHENG L Y, LI G Q, LI Z W. One-way hash function construction based on tangent-delay ellipse reflecting cavity-map system[J]. Acta Physica Sinica, 2006,55(11):5700-5706.

[10] LI S J, MOU X Q, et al. On the security of a chaotic encryption scheme: problems with computerized chaos in finite computing precision[J]. Computer Physics Communications, 2003, 153:52-58.

[11] 王繼志,王英龍，王美琴. 一類基于混沌映射構造散列函數方法的碰撞缺陷[J]. 物理學報，2006,55(10):5048-5054.WANG J Z, WANG Y L, WANG M Q. The collision problem of one kind of methods for constructing one-way hash function based on chaotic map[J]. Acta Physica Sinica, 2006,55(10):5048-5054.

[12] LIU J D. One-way hash function construction based on integer coupled tent maps[A]. International Symposium on Computer Science and Technology[C]. Ningbo, China, 2007.

[13] 劉建東,余有明. 基于可變參數雙向耦合映像系統的時空混沌散列函數設計[J]. 物理學報, 2007,56(3):1297-1304.LIU J D, YU Y M. A TCML-based spatiotemporal chaotic one-way散列 function with changeable-parameter[J]. Acta Physica Sinica,2007, 56(3): 1297-1304.

[14] 劉建東, 付秀麗. 基于耦合帳篷映射的時空混沌單向散列函數構造[J]. 通信學報，2007,28(6):30-38.Liu J D, Fu X L. Spatiotemporal chaotic one-way hash function construction based on coupled tent maps[J]. Journal on Communications,2007,28(6):30-38.

[15] HSIEH T M, YEH Y S, LIN C H, et al. One-way hash function with changeable parameter[J]. Information Sciences, 1999,118:223-239.

[16] LUNCKS S. Design principles for iterated hash functions[EB/OL].E-print Archive. http://eprint.iacr.org/ 2004/253.pdf, 2004.

[17] WEISTER A F, TAVARES S E. On the design of S-boxes[A]. Advances in Cryptology-CRYPTO’85[C]. Berlin: Springer-Verlag, 1986.523-533.

[18] 朱明富, 張寶東, 呂述望. 分組密碼算法擴散特性的一種統計分析[J].通信學報, 2002,23(10):122-128.ZHU M F, ZHANG B D, LV S W. A statistical method of blockcipher on diffusion & propagation[J]. Journal on Communications,2002,23(10):122-128.