布爾函數相關免疫性與平衡性關系的研究

李衛衛

（上海政法學院 現代教育技術中心，上海 201701）

1 引言

布爾函數的相關免疫性是保證密碼系統具有良好安全性的重要性質。布爾函數的導數（偏導數）的概念和性質是人們早已熟知的，但導數（偏導數）只能反映布爾函數內部一個方面值的結構特點。因而在討論布爾函數的相關免疫性時，沒有什么用途。在文獻[1,2]中引入布爾函數的e導數能刻畫布爾函數內部值的另一種特點的結構，將其和導數一起深入到布爾函數的內部結構中，從布爾函數內部不同特點的結構對相關免疫性的影響來分析布爾函數的平衡性與相關免疫性的關系，可得出有關布爾函數相關免疫性有意義的新結果，同時，也為更好地研究布爾函數的密碼學性質保證密碼系統的安全性指引了一個新的研究方向。

2 預備知識

首先，對e導數的概念和與本文有關的性質做簡要敘述。

定義1[1]布爾函數 f( x)的多元e導數為

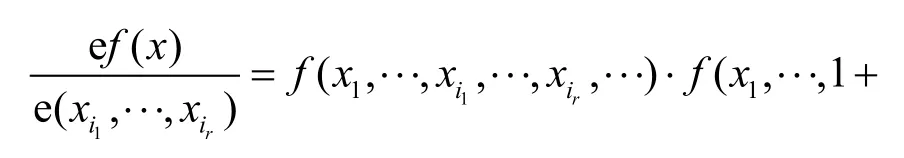
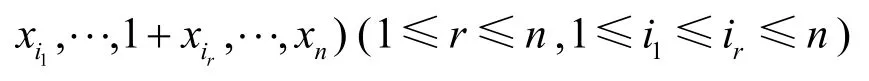
若r=1，則布爾函數f( x)對單個變元xi的e導數記為ef( x)/exi，即

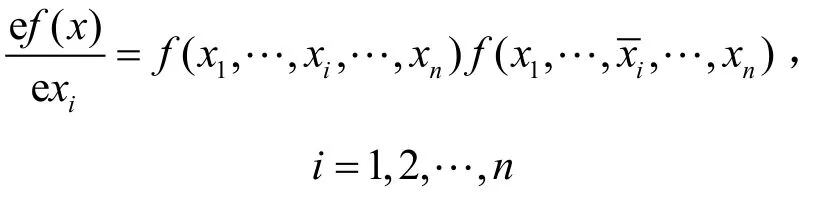
定義2[2]布爾函數f( x)對單個變元xi的導數記為df( x)/dxi，定義為

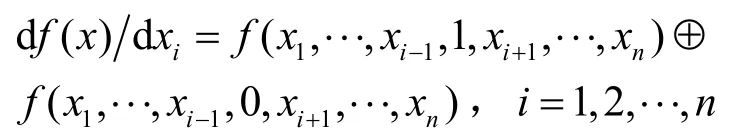
定義3[2]布爾函數f( x)對多個變元xi的導數記為df( x)/d(xi1,···xir),即

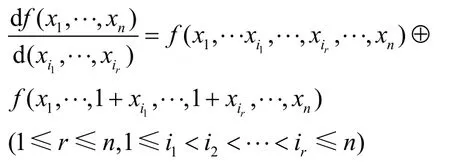
下面不加證明地給出2個有關導數和e導數的性質引理。

引理1[3]布爾函數f( x)是平衡H布爾函數，當且僅當w(df( x)/dxi)=2n-1，且w(e f( x)/exi)=2n-2,i=1,2,···,n

引理2[3]對布爾函數f( x),

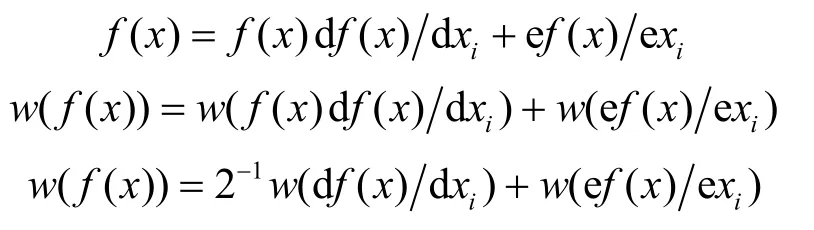
其取值范圍i=1,2,···,n。

3 平衡布爾函數的一階相關免疫性的判定

通過對平衡布爾函數一階相關免疫性的研究，可以簡化檢測平衡布爾函數是否一階相關免疫的計算，能很容易地構造高維一階相關免疫的平衡布爾函數，從而得出許多重要的密碼學性質定理。

定理1 n維平衡布爾函數f( x), x=(x1,x2,···,xn)由2個n-1維布爾函數fp(x)和fq(x)，其中x=(x1,x2,···,xn)級聯構成：f( x)=(1+x1)fp(x)+x1fq(x)。

1) 平衡布爾函數f( x)若有

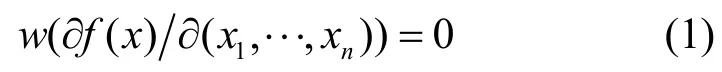
則f( x)是一階相關免疫函數。

2) 若平衡布爾函數f( x)是一階相關免疫函數，則w( fp( x))n-1=w( fq( x))n-1=2n-2,且w(e fp(x)exn)=w(e fq(x)exn)。

證明 ① 當式（1）成立，且f( x)是平衡布爾函數，則由偏導數的定義便知，對an∈GF(2)[3]（GF(2)表示伽羅華域），有w( f( x)|xn=an)=2-1w( f( x))=2n-2。取a∈GF(2)n,且w( a)=n，則式（1）等價于w( f( x+a)+f( x ))=0,f( x+a)=f( x)。故對任意xi, i=1,2,···,n ，有

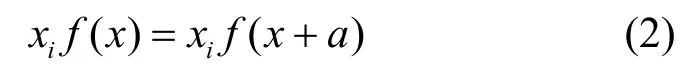
由于w( f( x))=w( xif( x))+w((1+xi) f( x))=2n-1，再由式（2）及f( x+a)的意義便知

故對任意xi, i=1,2,···,n ，有

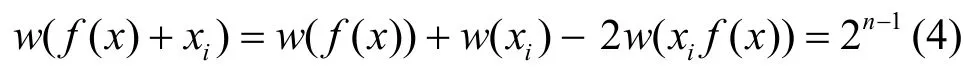
故知f( x)是一階相關免疫函數。

② 若f( x)是一階相關免疫的平衡布爾函數，則必有式（4）成立，于是在式（4）中，取xi為x1，便知

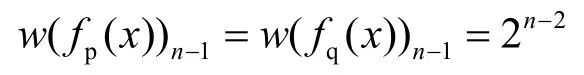
而在式（4）中，取xi為xn-1和1+xn-1，便知：w(e fp(x)exn)=w(e fq(x)exn)。

4 平衡布爾函數二階相關免疫性的判定及其構造

定理1說明一階相關免疫的平衡布爾函數（且非線性函數[4]）是易于構造的，那么是否存在并同樣易于構造出二階相關免疫的平衡布爾函數？下面來討論這一問題。給出一個平衡布爾函數一階相關免疫的充分性定理。

定理2 f( x)為平衡布爾函數，

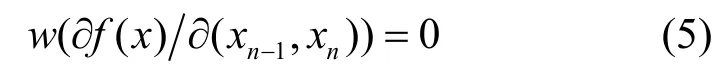
且w( ef( x)exn)=0，則f( x)是一階相關免疫函數。

證明 若式（5）成立，則f( x)在xx···x00～xx···x11取值范圍內對f( x)均有xn=0和xn=1處的值相等。又由于f( x)為平衡布爾函數，故對an∈GF(2)，有

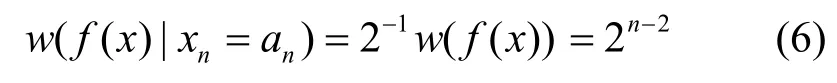
由于w(e f( x)/exn)=0，故f( x)在上述各取值范圍內的值均相等，均為

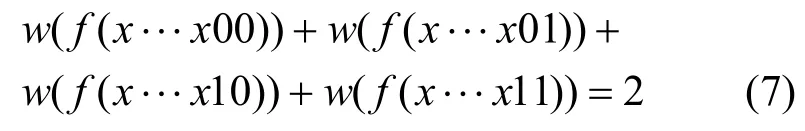
故知

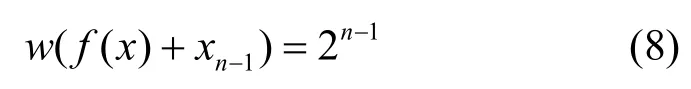
由各取值范圍內的值均相等及式（6）和式（7）可知，對xi( i≠n-1,n)也有

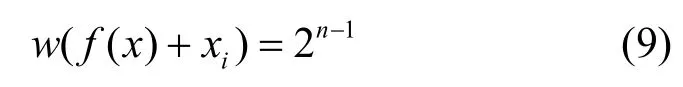
故由式（6）、式（8）和式（9）可知，對ai∈GF(2)n[5]，有w( f( x)|xi=ai)=2n-2，即f( x)是一階相關免疫的平衡布爾函數。

現在來討論平衡布爾函數二階相關免疫的判定問題。該問題也是在密碼學領域中一直沒有得到很好解決的難點問題之一，而下面的定理3、定理4給出了一個較之簡單的解決方法。同時，也給出了一個構造三階相關免疫[6]的平衡布爾函數的方法。

定理3 設g( x), x=(x1, x2,···,xn-2)是n-2元的一階相關免疫的平衡布爾函數，則n元布爾函數f( x)=g( x)+xn-1+xn是三階相關免疫的平衡布爾函數。

證明 先證明對任意n-2元布爾函數g( x),n元布爾函數f( x)=g( x)+xn-1+xn都是一階相關免疫的平衡布爾函數。

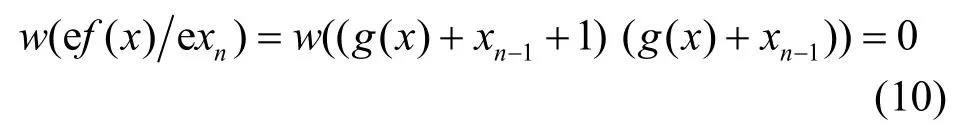
故w( f( x))=2-1w(df( x)dxn)+w(e f( x)exn)=2n-1，可知f( x)是平衡布爾函數。

由于

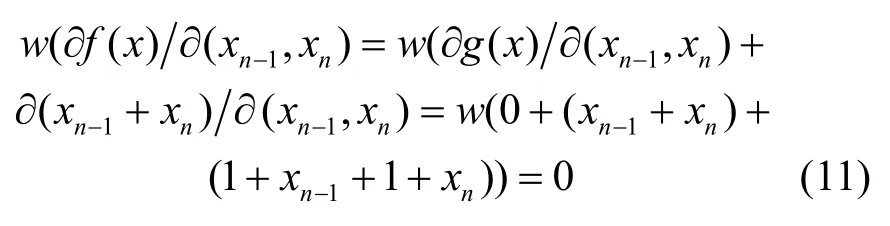
由f( x)是平衡布爾函數，式（10）和式（11）及定理2可知，f( x)是一階相關免疫的平衡布爾函數。于是有

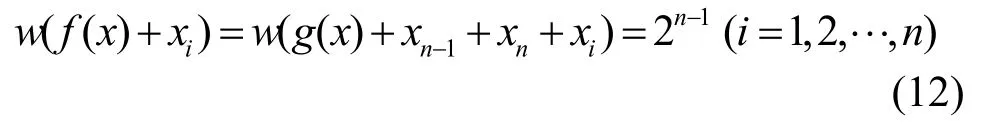
由開始處證明的結論便知，對i≠j(i, j=1,2,···,n -2)時，

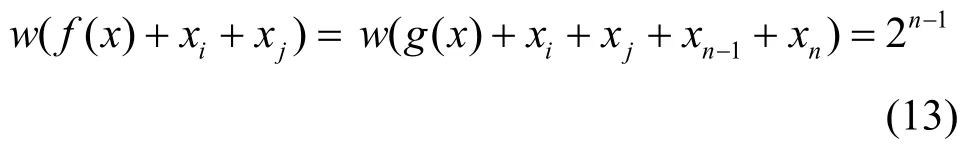
由式（12）知，對i≠j,當i=n-1,j≠n或i=n, j≠n -1時，由g( x)的任意性有

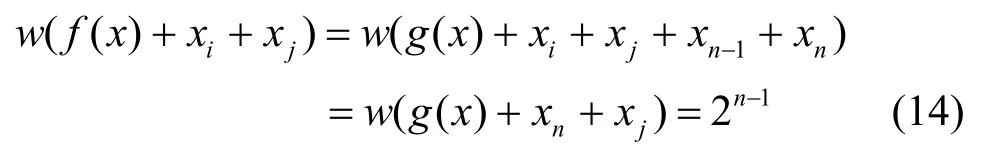
或

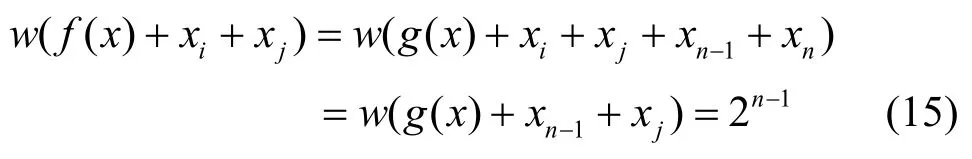
而當i=n-1,j=n時，由于g( x)是任意n-2元平衡布爾函數，故

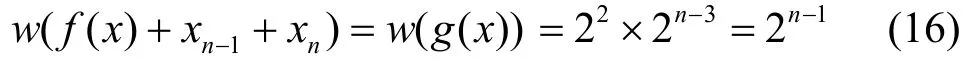
由式（13）～式（16）可知f( x)是二階相關免疫平衡布爾函數。

同樣，對i≠j≠k(i, j, k=1,2,···,n-2)，由開始的證明可知，g( x)+xi+xj+xk是與xn-1,xn無關的n-2元布爾函數。及

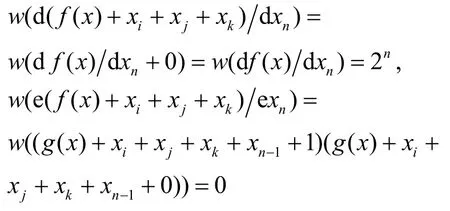
故

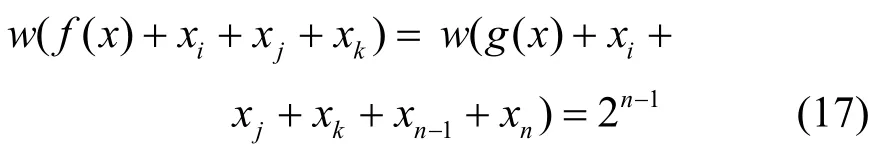
同樣由式（12）及式（12）中g( x)是任意n-2元布爾函數，故對i≠j≠k,i, j, k中有1個而且只有1個變元是xn-1或xn，而其余2個變元均不為xn-1或xn。不妨設xi=xn-1或xn，則有

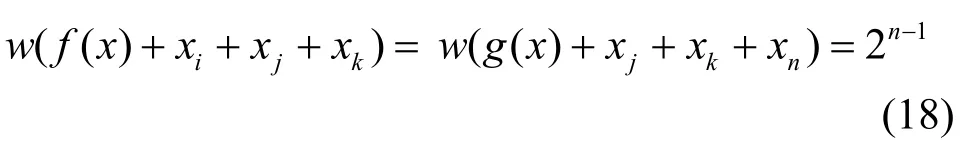
或

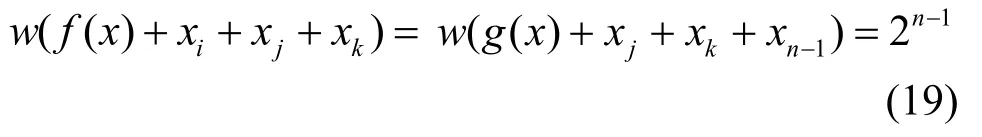
當i≠j≠k(i, j, k=1,2,···,n-2)，且i, j, k中有1個為xn-1，1個為xn時，不妨設xi=xn-1，xj=xn，由于g( x)是一階相關免疫函數，故有

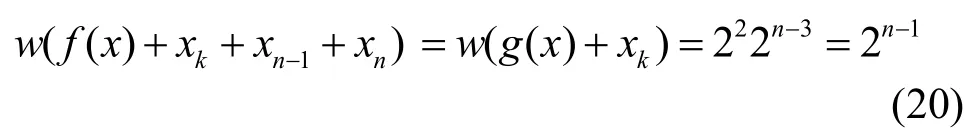
由式(17)～式(20)可知，f( x)是三階相關免疫的平衡布爾函數。

從定理3的證明，顯然可得到如下推論。

推論1 設g( x), x=(x1, x2,···,xn-2)是n-2元的平衡布爾函數，則n元布爾函數f( x)=g( x)+xn-1+xn是二階相關免疫的平衡布爾函數。

推論2 設g( x), x=(x1, x2,···,xn-2)是n-2元布爾函數，則n元布爾函數f( x)=g( x)+xn-1+xn是相關免疫的平衡布爾函數。

定理3實際上給出了一個構造三階相關免疫的平衡布爾函數的方法[7]。判斷一個平衡布爾函數是二階相關免疫函數，判斷工作量是很大的，但定義了e導數以后，可以得到一個判斷平衡布爾函數二階相關免疫的較簡單方便的方法。因此有下面的定理。

定理4 設f( x)為非線性布爾函數，若

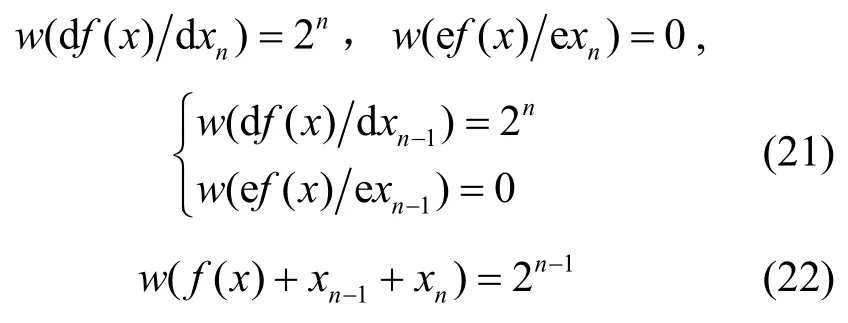
則f( x)是二階相關免疫的平衡布爾函數。

證明 由式（21）便知，f( x)是平衡布爾函數。

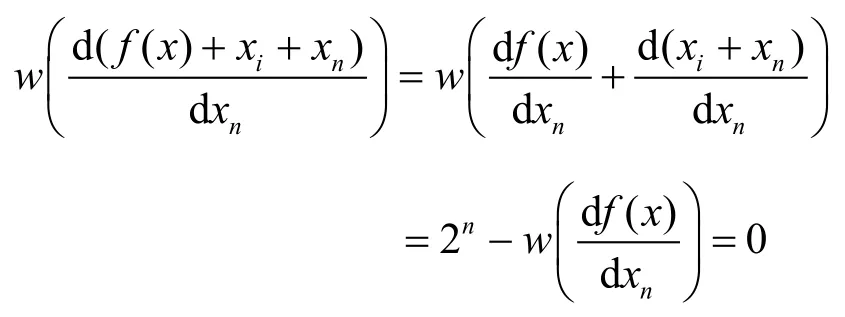
故f( x)+xi+xn一定與xn無關，所以f( x)一定為如下函數f( x)=g( x)+xn（其中g( x)與xn無關）。

同樣由于w(df( x)dxn-1)=2n，故對i=1,2,···,n-1,n，有

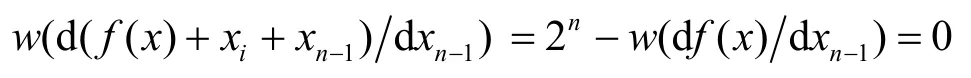
因此，f( x)+xi+xn-1一定與xn-1無關，故f( x)一定是如下函數。

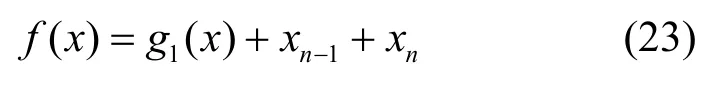
其中，g1( x)+xn-1=g( x)，且g1( x)是與xn-1及xn無關的非線性函數。

由式（23）及推論2，便知f( x)是一階相關免疫的平衡布爾函數。當i, j=1,2,···,n-2，且i≠j（其中r=n-1或r=n）。有

故知

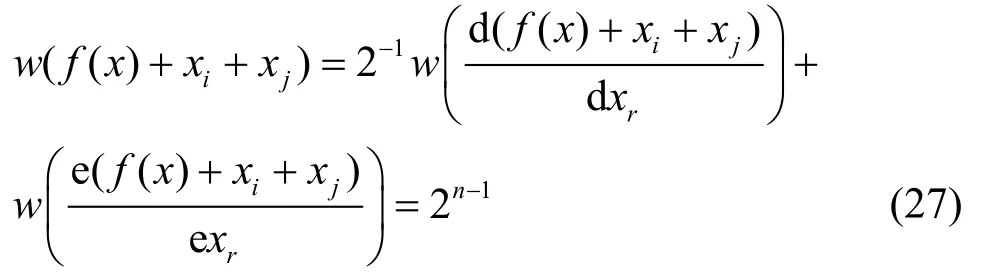
取xj=xn-1,i=1,2,···n-1,n，有

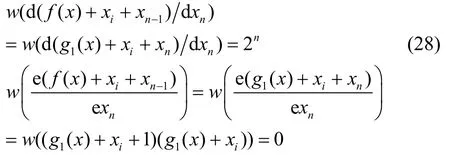
故

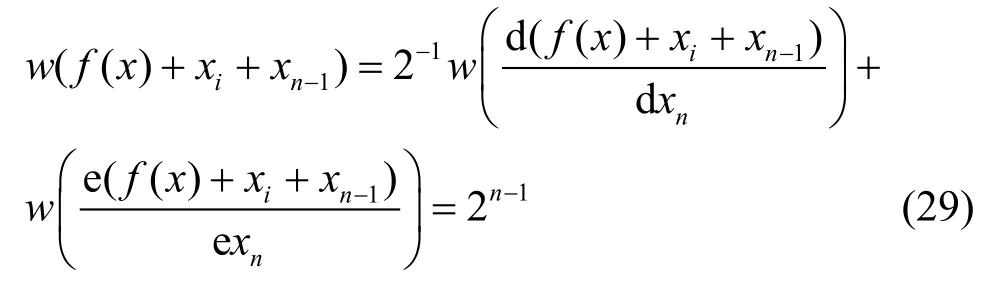
同理，取xj=xn,i=1,2,···,n -1，也有

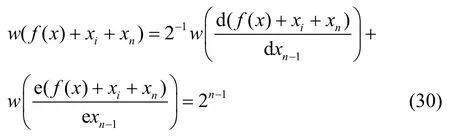
于是由式（27）、式（29）、式（30），便知對一切i=1,2,···,n-1,n,且i≠j，均有式（22），即w( f( x)+xi+xj)=2n-1，故知f( x)是二階相關免疫的平衡布爾函數。證畢。

由定理4的證明，還可得到如下推論。

推論3 設f( x)為非線性平衡布爾函數，若式（21）成立，則：

1) f( x)是一階相關免疫的平衡布爾函數；

2) f( x)一定為式（23），即f( x)=g1( x)+xn-1+xn（其中g1( x)是與xn-1、xn無關的n-2元布爾函數）；

3) 式若（27）成立，則g1( x)是n-2元平衡布爾函數。

推論3的第1個和第2個結論在定理4中已給出了詳細的證明，而第3個結論只需要由w( f( x)+xn-1+xn)=w( g1( x))n=2n-1，即知w( g1( x))n-2=2(n-2)-1，故結論成立。

由定理3和定理4顯然還可得到如下推論4。

推論4 若f( x)是三階相關免疫的平衡布爾函數，且滿足定理4的式（21）和式（22），則：f( x)=g1( x)+xn-1+xn，其中g1( x)是與xn-1、xn無關的n-2元一階相關免疫的平衡布爾函數。

從定理3和定理4的證明中可看出，在定理的這種構造相關免疫函數的方法中，擴散性[8]對免疫性沒有影響。

5 結束語

從文中的討論及結論可知，用e導數（e偏導數）和導數（偏導數）深入到布爾函數的內部結構中，可以較容易地得到相關免疫性的有意義的結論，得出一些有用的且能揭示滿足相關免疫性的平衡布爾函數結構特點的性質，如判斷相關免疫性、構造相關免疫函數等密碼系統所需的內容[9～11]。進一步揭示了布爾函數優良的密碼學性質，為更好地研究布爾函數的密碼學性質保證密碼系統的安全性和抗攻擊性打下了基礎。

[1] LI W W, WANG Z. The E-derivative of Boolean functions and its application in the fault detection and cryptographic system[A]. The 5th IIGSS Workshop, Kybetrnetes[C]. 2007.245-249.

[2] 溫巧燕, 鈕心忻, 楊義先. 現代密碼學中的布爾函數[M]. 北京: 科學出版社, 2000. 31-33.WEN Q Y, NIU X X, YANG Y X. Boolean Function in Modern Cryptoloy[M]. Beijing: Science Publishing House, 2000. 31-33.

[3] 李衛衛, 王卓. E-導數和導數在布爾函數中的應用[A]. 中國通信學會第五屆學術年會論文集[C]. 2008.267-270.LI W W, WANG Z. The application of derivative and E-derivative on H-Boolean functions[A]. The 5th China Institute of Communications Collected Papers[C]. 2008. 267-270.

[4] GUO Y F, LAN L Y. Balanced correlation-immune functions[J]. China Science and Technology Information, 2006, 20(8): 22-25.

[5] XIAO G Z, MASSEY J L. A spectral characterization of correlation-immune combining functions[J]. IEEE Trans on Inform Theory,1988, 34(3): 725-728.

[6] MO J. The construction and enumeration of symmetric balanced Boolean functions[J]. Journal of Beijing University of Posts and Telecommunications, 2006, 29(5): 5-8.

[7] 張串絨, 肖國鎮. 一類布爾函數的性質和應用[J]. 通信技術,2001,16(2):11-14.ZHANG C R, XIAO G Z. Properties and applications of a class of Boolean functions[J]. Communications Technology, 2001, 16 (2):11-14.

[8] HE L S. On Boolean functions with highest algebraic immune degree[J]. Chinese Journal of Computers, 2006, 29(9): 1579-1583.

[9] ZHANG W G, XIAO G Z. A characterization of algebraic immune Boolean functions[J]. Journal of Beijing University of Posts and Telecommunications, 2007, 30(5): 56-57.

[10] LUO W H, LI C. Algebraic immunity study of Boolean functions[J].Computer Engineering and Applications, 2007, 43(8): 59-60.

[11] SIEGENTHALER T. Correlation-immunity of nonlinear combining functions for cryptographic applications[J]. IEEE Trans, 1984, 30(5):776-778.