加筋結構非節點連接建模中鋼筋單元劃分方法研究

彭 毅，王家林，易志堅，李 平

(重慶交通大學土木建筑學院，重慶400074)

目前，加筋結構的有限元建模方法主要有分離式、整體式和組合式3種［1］。

分離式模型對加筋結構和基體材料分別劃分單元，通過節點連接重構整體。在建模過程中，分離式模型要求加筋單元和基體材料單元共用節點，建模難度大，可能造成兩個結果的出現:①加筋構件的布置與實際不符，在計算結果上出現虛假的應力集中;②基體單元的形狀不規則［2］，導致計算結果不準確。

整體式模型將加筋構件均勻彌散于整個基體材料單元中，通過各方向的配筋率來計算加筋構件對基體材料的增強效果。這種方法計算簡便，但是對加筋構件的布置細節反應不足，更無法模擬有滑移的情況。

組合式模型克服了分離式模型建模難度大和整體式模型過于粗略的特點，為加筋結構的有限元分析提供了一種切實可行的方法。但是，組合式單元模型要求加筋單元與基體材料單元位移連續、變形協調，當兩者之間存在位移不連續時，組合式難于處理［3］。

針對以上3種有限元建模方法各自存在的不足，王家林［4］提出了具有一般意義的不通過節點連接的有限元建模和分析方法，即非節點連接方法，并開發了以非節點連接有限元理論為基礎的有限元軟件RCF。非節點連接方法在處理加筋結構的問題時，可以方便的模擬加筋構件的黏接滑移問題。本文針對加筋結構中鋼筋單元跨越多個混凝土單元的情況，在非節點連接理論的框架內分析了筋元與混凝土單元的位置關系，并對筋元與混凝土單元面的交點建立了數學模型，解決了鋼筋單元與混凝土單元之間的位移協調問題。

1 筋元與混凝土單元位置關系分析

在加筋結構模型中，一個鋼筋單元跨越兩個或多個混凝土單元的現象較為常見。由于一個筋單元跨越兩個混凝土單元是最基本的筋元跨越問題，因此，有必要對這一問題進行細致分析。

如圖1，筋單元AB跨越混凝土單元①及混凝土單元②。筋元A節點作為混凝土單元①的內節點進行分析，筋元B節點作為混凝土單元②的內節點進行分析，在非節點連接理論中，內節點位移由母單元各節點位移插值決定。由于筋元內部各處位移由筋元兩端節點位移插值得到，而筋元兩端節點又作為混凝土單元內節點，因此，AB段鋼筋單元內各處的位移由兩個混凝土單元的節點位移插值決定［5］。

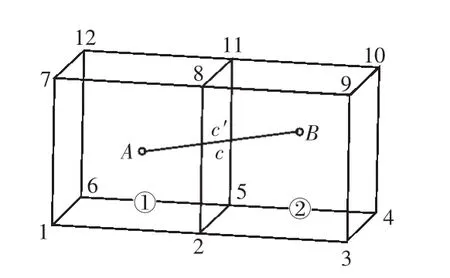
圖1 加筋結構單元模型Fig.1 The element model of reinforced structures

在筋元與混凝土單元面的相交處，筋元上的C點與混凝土單元面上C′點重合。C點位移由混凝土單元①和混凝土單元②的各節點位移共同插值決定，C′點的位移由兩混凝土單元交面各節點位移插值決定，這使得筋元與混凝土單元之間的位移存在一定的不協調性。

為改善上述不協調性，可以設置筋元上的C點為混凝土單元的內節點。作為鋼筋單元與混凝土單元面的交點，C節點既可以作為其左側混凝土單元①的內節點又可以作為其右側混凝土單元②的內節點。由于單元面上各點的位移僅與單元面各節點的位移有關，因此無論將C節點作為哪個單元的內節點，均不會產生差別。

C節點的引入，使得原有的一個鋼筋單元AB被劃分成兩個單元，即鋼筋AC單元和鋼筋CB單元，如圖2。鋼筋AC單元包含于混凝土單元①內，鋼筋CB單元包含于混凝土單元②內。

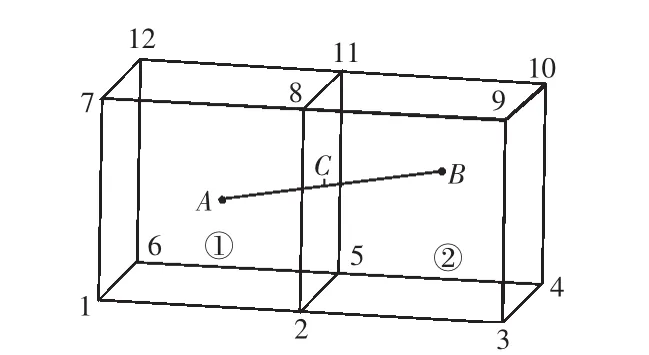
圖2 鋼筋設置交點以后的結構單元模型Fig.2 The steel element interpolating a intersection

經過插入節點分段后，AC段筋元內的位移由其所在的混凝土單元①各節點位移插值決定，CB段筋元內的位移由其所在的混凝土單元②各節點位移插值決定，由此，鋼筋單元與混凝土單元的位移插值關系便滿足了位移的協調性要求。

2 筋元與混凝土單元位置關系

混凝土單元作為等參元，其體內未知點的位移由單元形函數插值得到。對筋單元的數值模擬一般采用線性插值［6］。筋元與混凝土單元相交情況如圖3。

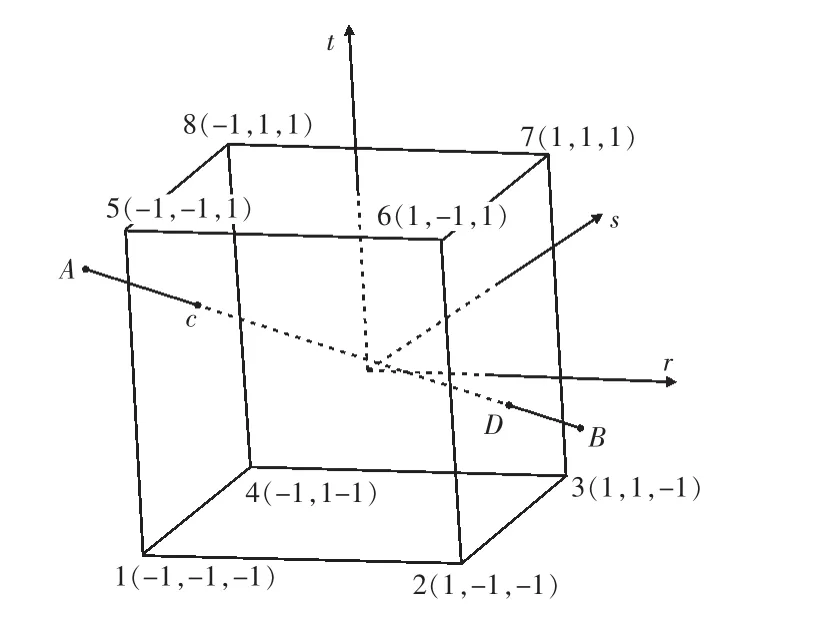
圖3 筋元與混凝土等參元相交模擬Fig.3 The intersection simulation of steel element and concrete element

由關鍵點 A(xm，ym，zm)，B(xn，yn，zn)所確定的鋼筋段的參數方程為:

a∈［0，1］，為鋼筋單元位置參數。

混凝土等參元坐標變換方程為:

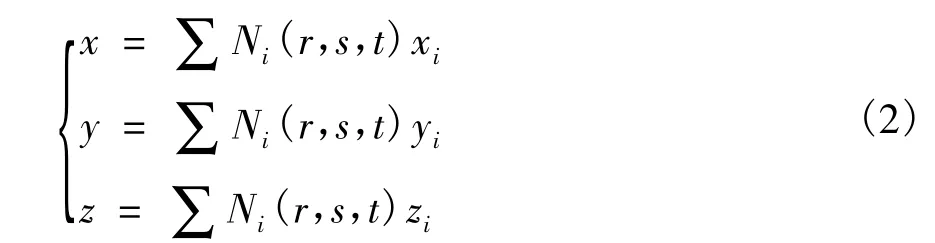
Ni(r，s，t)為混凝土單元內i節點的形函數。

xi，yi，zi為混凝土單元 i節點的位移。

在求鋼筋單元與混凝土單元面交點的過程中，將兩參數方程聯立求解可得到交點坐標:

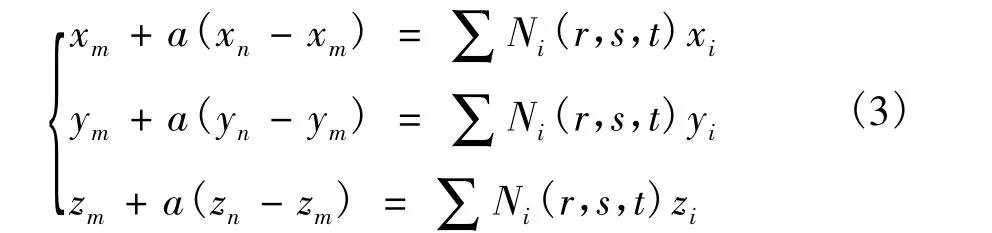
其中，r∈［－1，+1］;s∈［－1，+1］;t∈［－1，+1］，任一參數取+1或－1表示某一單元面。

以求解鋼筋與混凝土等參元幾何面r=1上的交點為例。

令:

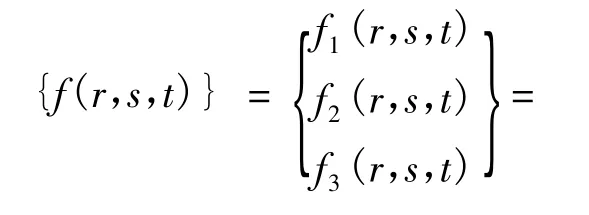
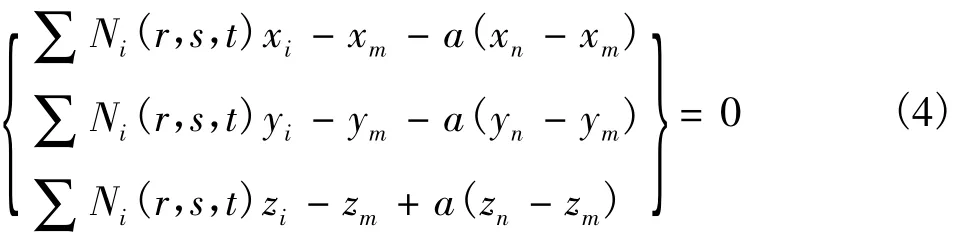
設(sn，tn，an)為方程的第 n 次近似解，將 {f(r，s，t)} 在 (sn，tn，an)處近似展開得:

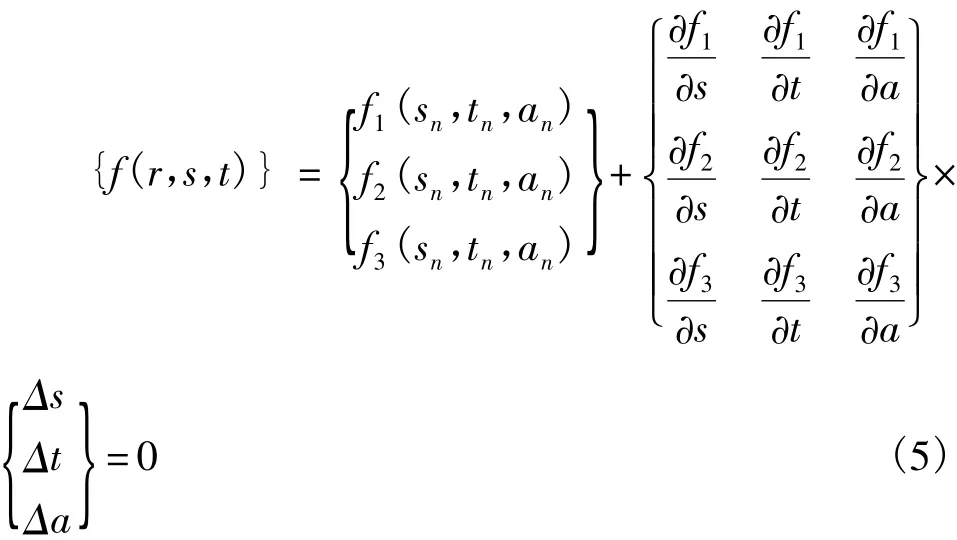
于是得到下面遞推公式:

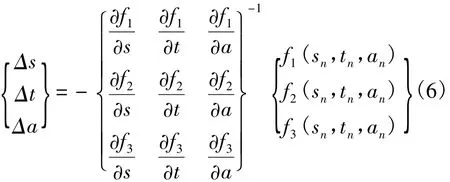
也即:

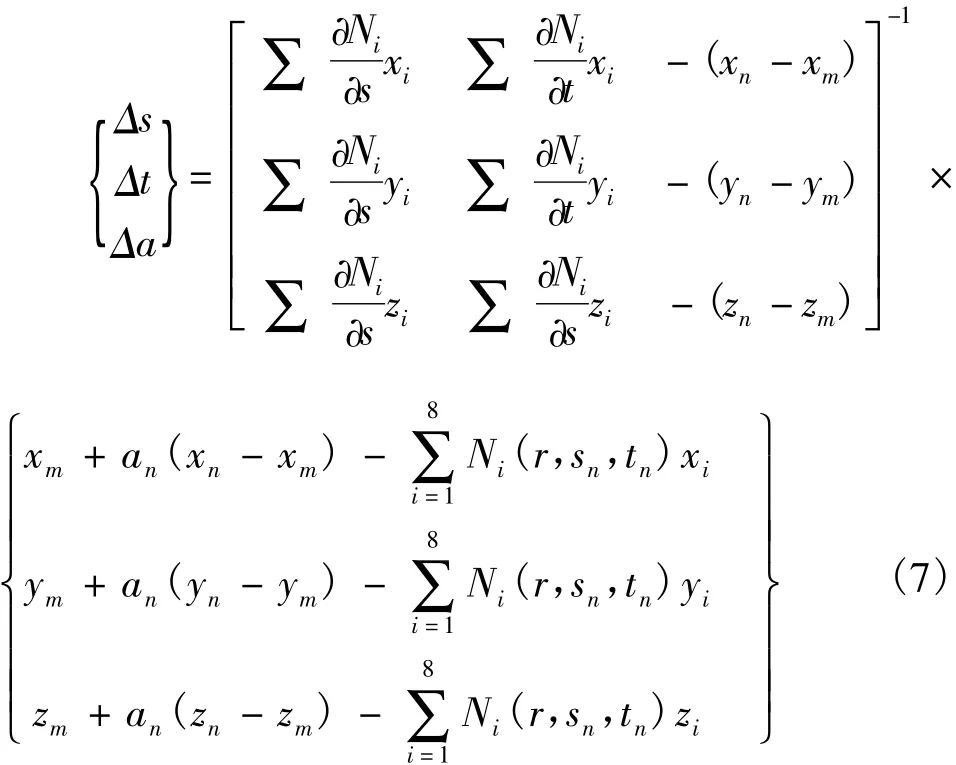
由式(7)，通過迭代計算可得到鋼筋與混凝土單元面交點的局部坐標(r，sn+Δs，tn+Δt)以及交點在鋼筋直線方程中的比例系數(an+Δa)。

再通過混凝土等參元坐標轉換方程得到交點的整體坐標:

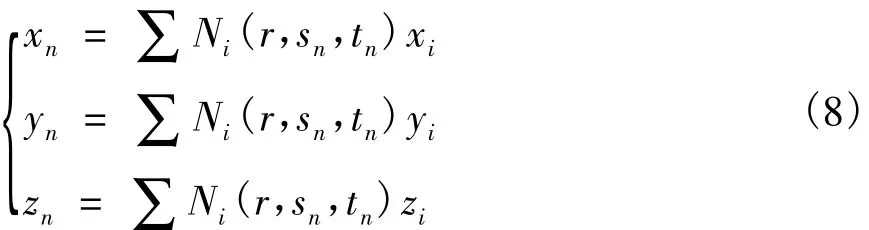
以上所采用的數值計算方法易于在計算機上實現，具有計算速度快，收斂性好等優點。

3 算例

如圖4矩形截面簡支梁，梁段全長L=6 m，截面高h=0.4 m，寬b=0.2 m，鋼筋直徑d=0.02 m，BC段和DE段為鋼筋彎起段，彎起半徑為3 m，鋼筋B端和E端到截面底邊的距離為0.18 m，CD段鋼筋到截面底邊的距離為0.04 m。取混凝土彈性模量Ec=2.0×104MPa，泊松比v=0.2鋼筋彈性模量Es=2.0×105MPa，在梁的上表面作用有集度為q=500 kN/m2的均布荷載。

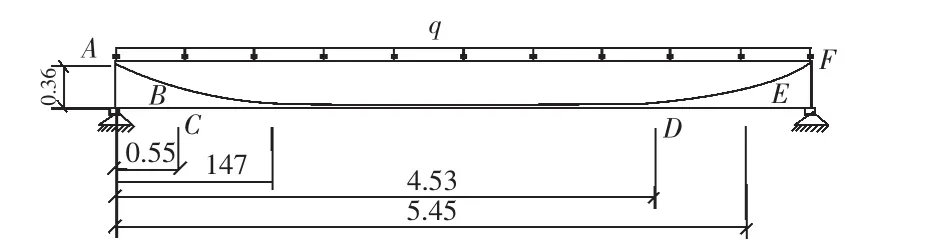
圖4 受分布荷載的鋼筋混凝土簡支梁Fig.4 The reinforced concrete simple beam subject to distributed load

在混凝土結構中加入導線法線形鋼筋，并用RCF軟件計算鋼筋混凝土結構中鋼筋的受力狀態。考慮鋼筋主要以軸向受力為主，鋼筋單元采用桿單元模擬［7］。

結構的網格劃分按如下方式完成。沿梁的長度方向劃分為20個三維8節點等參體元，鋼筋網格單元長度設置為0.2 m。全部鋼筋單元的節點用軟件自動分析找到母單元，并設置全部自由度與母單元位移場一致。

為了充分反應加入交點后筋元與混凝土單元的位移協調關系，圖5將未插入交點時筋元與體元面相交處兩者位移的差值和插入交點后筋元與體元面相交處兩者位移的差值進行比較［8］。

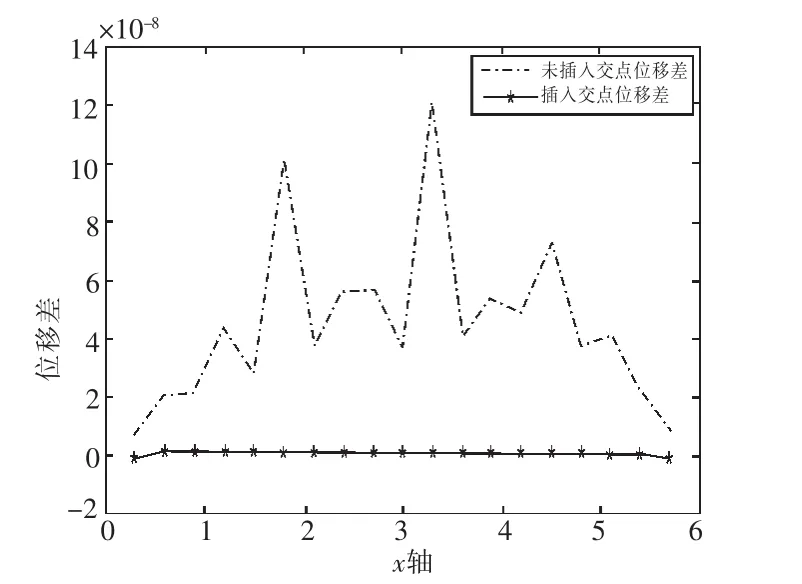
圖5 位移差對比Fig.5 Comparison chart of displacement difference

未插入交點位移差代表了未插入交點時筋元與體元面相交處兩者位移的差值，插入交點位移差代表了插入交點后筋元與體元面相交處兩者位移的差值。由圖5可以看出，界面未設置交點時，位移差雖很小，但存在，表明鋼筋與混凝土單元之間位移的不協調性。插入交點后，完全消除了兩者的位移差，實現了二者的位移協調。

4 結論

通過算例演示了非節點連接方法中筋元與體元在單元交界面處的位移協調性。采用在筋元與體元面相交處插入交點的方法，消除了筋元與體元之間位移的不協調性，可進一步實現加筋結構有限元的精細分析。

［1］王勖成.有限單元法［M］.北京:清華大學出版社，2003.

［2］李青森，楊文兵，楊新華.預應力梁的組合結構分析方法及其有限元實現［J］.華中科技大學學報:城市科學版，2005，22(增刊):84－90.

［3］江見鯨.鋼筋混凝土結構非線性有限元分析［M］.西安:陜西科學技術出版社，1994.

［4］王家林.非節點連接有限元理論及其軟件實現［D］.重慶:重慶大學，2008.

［5］王家林.鋼筋混凝土結構空間有限元分析的體梁組合單元［J］.工程力學，2002，19(6):131 －135.

［6］巫昌海.三維鋼筋混凝土非線性有限元及其工程應用研究［D］.南京:河海大學，2000.

［7］El-Mezaini N，Citipitioglu.Finite element analysis of prestressed and reinforced concrete structures［J］.Journal of Structural Engineering，ASCE，1991，117(10):2851－2864.

［8］朱橫君.MATLAB語言及實踐教程［M］.北京:清華大學出版社，北京交通大學出版社，2005.