聯方—凱威特型弦支穹頂靜力特性參數分析
屈訟昭 王志騫
弦支穹頂是一種復合結構,影響其靜力性能的因素比較多,下面即針對聯方—凱威特型弦支穹頂分別從矢跨比、預應力、節點剛度3個因素進行參數分析。
1 計算模型
計算模型跨度為99 m,內圈凱威特部分徑肋數量為6,外圈聯方部分徑肋數量為48,整個模型的環桿圈數為16。矢跨比為1/6,下部索從最外圈向內連續布置8圈,環撐桿的高度從里圈到外圈依次為:內四圈為4.5 m,最外兩圈為7.0 m,其余的為5.5 m(見圖1)。桿件為圓鋼管,上部單層網殼部分采用截面299×8,下部支撐豎桿采用鋼管截面為219×7,斜向拉桿采用鋼拉桿A80,環索采用半平行鋼絲束A7×73。鋼管的彈性模量為E=2.06×1011N/m2,索的彈性模量為E=1.9×1011N/m2,上部單層網殼節點采用剛接,下部豎桿與網殼的連接節點和豎桿與索的連接節點都采用鉸接。上部單層網殼桿件采用Beam4單元,下部支撐體系徑向拉桿和豎向撐桿采用Link8單元,環索采用Link10單元模擬。支撐方式為周邊固定鉸支支撐,荷載為全跨面荷載2 kN/m2,預應力水平T=1 373 kN。
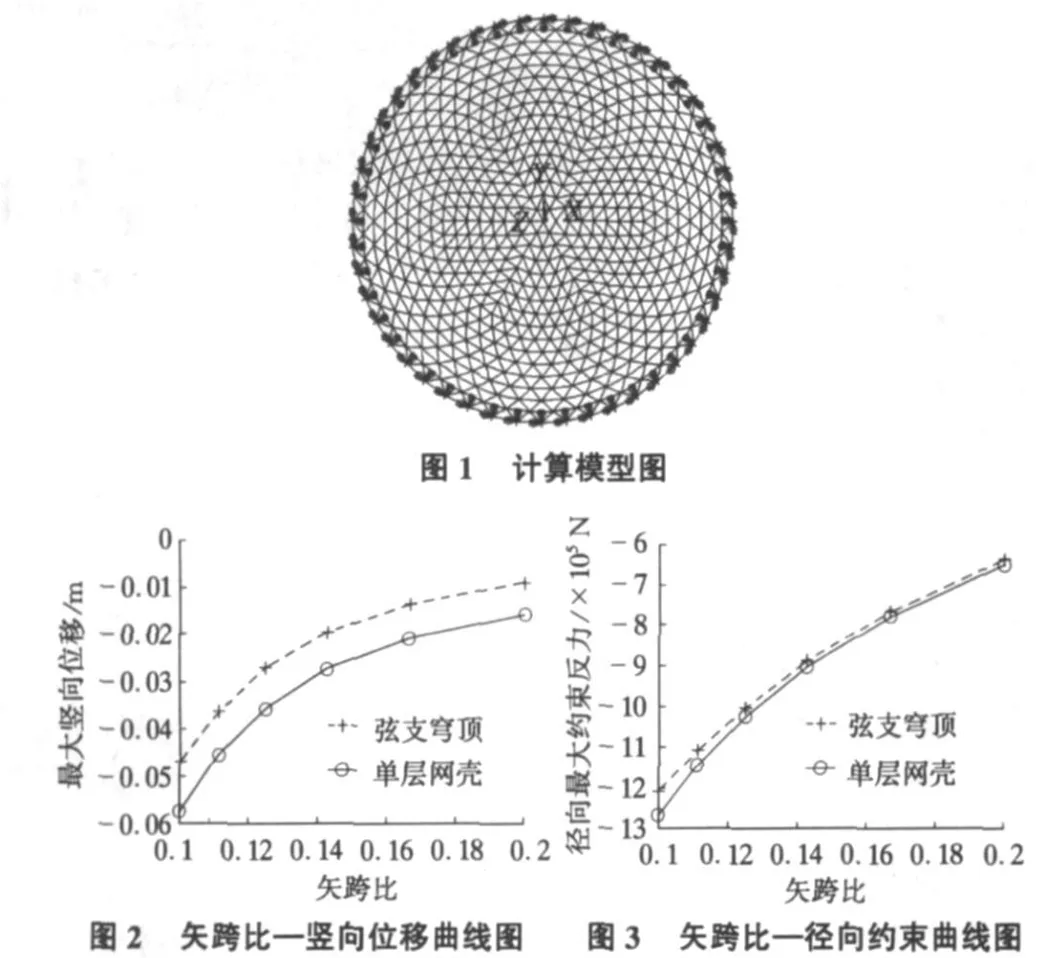
2 弦支穹頂結構參數分析
2.1 矢跨比對靜力性能的影響
分別以矢跨比為1/5,1/6,1/7,1/8,1/9,1/10六種情況,將弦支穹頂結構與對應的單層網殼結構進行對比分析,從而確定矢跨比對結構靜力性能的影響。在矢跨比變化的范圍內,弦支穹頂的最大豎向位移始終低于單層網殼的最大豎向位移。但在矢跨比為0.1時兩者之間的差值為0.01 m,在矢跨比為0.2時兩者之間的差值為0.007 m。可見在矢跨比較小的情況下,弦支穹頂結構的優越性表現的比較明顯(見圖2)。
在矢跨比為0.1時,兩者之間的差值為59.32 kN;當矢跨比為0.2時,兩者之間的差值為13.90 kN。可見,當矢跨比較小時弦支穹頂的優越性更加顯著(見圖3)。
隨著矢跨比的增加,弦支穹頂對桿件內力均勻化的效果越明顯,弦支穹頂上部單層網殼結構桿件的最大內力與單層網殼桿件最大內力差值越大。因此對于從提高桿件受力均勻性這點來說,弦支穹頂改善矢跨比較大的單層網殼的作用更加明顯。
2.2 預應力水平對靜力性能的影響
隨著預應力水平的提高,弦支穹頂結構上部單層網殼節點豎向位移逐漸減少,但是改變的范圍很小,所以預應力水平對結構最大豎向位移的影響是可以忽略的。預應力的增加,對結構的整體剛度是沒有影響的(見圖4)。
整個過程中前期徑向支座約束反力都處于推力狀態,但是從T=6 000 kN到T=8 000 kN徑向約束反力從推力變到了拉力,也就是在其之間有一點是可以將徑向約束反力控制在很小值的。可見,預應力的施加,對于減小徑向約束反力效果很明顯。可以通過改變弦支穹頂下部支撐體系中索的預應力的大小,盡可能消除徑向約束(見圖5)。
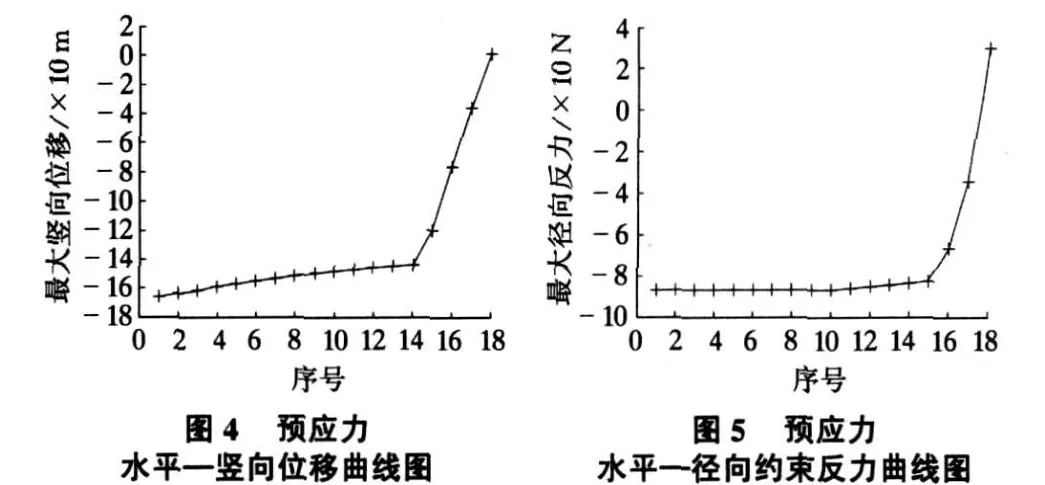
弦支穹頂上部單層網殼桿件內力絕對值最大值都隨著預應力水平的提高有減小的趨勢。
2.3 上部桿件節點的選取方式對靜力性能的影響
分別就桿件鉸接連接和剛接連接兩種不同模型下對靜力性能研究,將原有模型上部單層網殼對應下邊有支撐體系的剛接桿件換成鉸接,并與全部為剛接的原模型計算出的結果進行比較。
豎向位移變化量最大的分別為:269號節點變化量為2.43%,458號節點變化量為-5.381%。可見兩種不同的單元建造的模型對最終計算的位移值影響不大。
桿件內力變化量最大的分別為:169號桿件變化量為0.24%,937號桿件變化量為-0.33%。可見,兩種不同的單元組建的計算模型對桿件內力的影響很小。
徑向約束變化量最大的為0.024%。切向約束變化量最大為-1.92%。豎向約束變化量最大為-0.000 1%。可見兩種不同單元組建的模型對支座反力的影響微乎其微。
3 結語
1)在變形和徑向支座反力上弦支穹頂結構對于改善矢跨比較小的單層網殼的效果是比較明顯的。但是在改變上部單層網殼桿件內力分布,使其受力更加均勻方面矢跨比越大改善的效果越明顯。2)預應力水平對弦支穹頂上部單層網殼豎向變形影響不大,徑向支座反力隨著預應力水平的提高減小的比較明顯。桿件內力隨著預應力水平的提高變化不明顯。3)對于下部有支撐體系的上部單層網殼的桿件節點,選用剛接或者選用鉸接對計算的結果影響很小。
[1]張明山.弦支穹頂結構的理論研究[D].杭州:浙江大學博士論文,2004:30-43.
[2]郭佳民.弦支穹頂結構的理論分析與試驗研究[D].杭州:浙江大學博士論文,2008:51-54.
[3]姚 姝,范 峰.K6型弦支穹頂結構的靜力性能分析[J].建筑結構,2008,38(2):43-46.

