線性規劃法在水資源系統規劃優化配置中的應用
康永輝,王寶紅
(廣西水利電力勘測設計研究院,廣西 南寧 530023)
1 線性規劃簡介
線性規劃是運籌學中應用最為廣泛的一個分支,也是運籌學最基本的部分。線性規劃是研究在現有人力、物力等資源條件下,合理調配和有效使用資源,以達到最優目標(產量最高、利潤最大、成本最小、資源消耗最少等)的一種數學方法。目前已廣泛應用于生產管理、資源分配、運輸問題、生產計劃問題、環境保護、軍事等眾多領域。線性規劃的數學理論成熟、建模簡單,有通用算法和計算機軟件進行計算。一般首先根據研究問題的性質確定決策變量;根據問題的目標,列出與決策變量有關的目標函數;根據問題的限制條件,列出與決策變量有關的約束條件來建立數學模型。線性規劃的求解有圖解法和單純形法,在實際應用中一般采用單純形法進行求解。
2 線性規劃模型及求解
線性規劃模型一般由3個要素組成:①變量,或稱決策變量,是問題中要確定的未知量,它用以表明規劃中的用數量表示的方案、措施,可由決策者決定和控制;②目標函數,它是決策變量的函數,按優化目標分別在這個函數前加上 max或min;③約束條件,指決策變量取值時受到的各種資源條件的限制,通常表達為含決策變量的等式或不等式。
線性規劃模型可以表示為:
(1)求和形式:
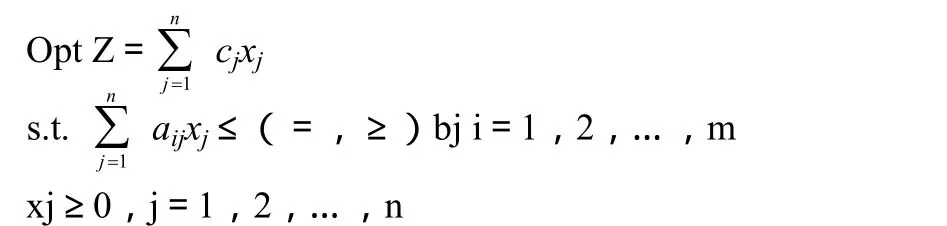
(2)矩陣形式:
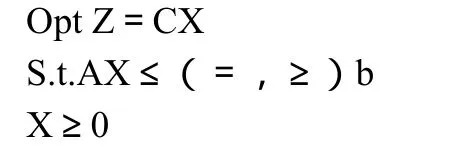
(3)集合形式:
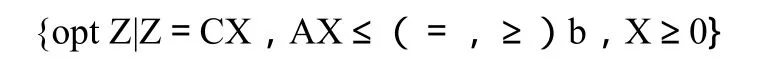
其中:“s.t”(subject to的縮寫)表示約束于;“opt”表示最優的意思,一般是max或min。
求解一般線性規劃問題有圖解法和單純形法。圖解法是求解線性規劃的一種直觀方法,可用于解決含有兩個決策變量的線性規劃問題,其目的是判別線性規劃問題的求解結局和存在最有解的條件下,把問題的最有解找出來。圖解法的步驟可概括為:在平面上建立直角坐標系,兩個坐標軸對應于兩個決策變量;圖示約束條件,找出可行域;圖示目標函數和尋找最優解。
根據線性規劃解的基本定理,線性規劃問題的可行域為凸集或無界域(如果可行域不為空集);凸集有有限個頂點,每個基可行解對應于一個頂點;若線性規劃模型有最優解,必定在某個頂點上取得。對于決策變量數n、約束方程數m比較小的情況,可以采取枚舉法,通過比較有限個基可行解的目標函數值來確定最優解與最優值。但對于 n、m比較大的情況,完全枚舉法的計算量較大,這就需要采用更有效的方法——單純形法(simplex method)來求解線性規劃模型。
單純形法的求解思路是:對于給定的 LP模型,從某個基可行解(可行域的一個頂點)開始,按照一定的規則轉換到另一個基可行解(頂點),使新頂點的目標函數值優于原目標函數值,經過有限次迭代直至目標函數達到最優。需要解決3個關鍵問題:初始基可行解(頂點)的確定;基可行解的轉換規則;最優行判斷準則。單純形法的計算步驟主要包括:①將 LP模型轉換為標準型;②求初始基可行解,列出初始單純形表;③求得初始基可行解后進入迭代過程,在每一次迭代過程中還包括根據最優性條件確定最優解或換入變量和根據可行性條件確定換出變量兩步。確定新的基可行解后繼續進行迭代,經過有限次迭代后就可以找到最優解。
3 用線性規劃模型優化配置水資源
某供水工程年供水能力為6 500萬m3,主要用于工業、農業以及生活用水,有關需水量、水價、供水成本、供水要求見表 1。由于向不同部門供水的水價以及供水成本不一樣,因此利潤也不樣,在滿足供水要求的情況,就需確定最優配水方案,才能使供水效益最大。
3.1 決策變量的確立
主要向工業、農業、生活三部門供水,因而可確定工業、農業、生活用水量為決策變量,分別為X1、X2、X3。
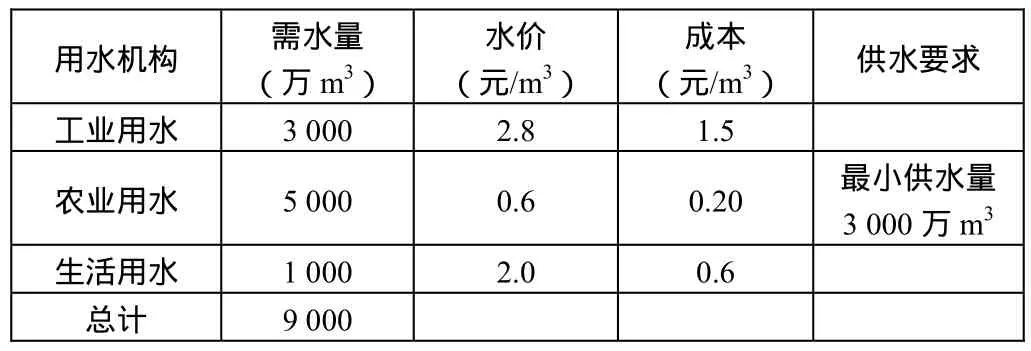
表1 需水量、水價、供水成本、供水要求表
3.2 目標函數的建立
根據有關部門的用水量要求,以及水價和成本來確定最優分配方案,使供水效益最大,即Max Z=(2.8-1.5)X1+(0.6-0.25)X2+(2.0-0.6)X3。
3.3 約束方程
(1)三部門的總用水量小于供水工程總供水量,即:
X1+X2+X3≤6 500
(2)三部門的最大用水量限制
X1≤3 000,X2≤5 000,X3≤1 000。
(3)三部門的最小用水量限制
X1≥0,X2≥3 000,X3≥0。
3.4 求解
由于該模型含有3個決策變量,不便于用圖解法來求解,可采用單純形法來求解,按照單純形法的求解步驟及要求可求得目標值為5 700萬元,達到最優解時的各變量值分別為:X1=2 500萬m3、X2=3 000 萬 m3、X3=1 000 萬 m3。也可以利用 Microsoft Excel 規劃求解工具進行規劃求解,Microsoft Excel 規劃求解工具可用于求解一定限制條件下目標單元的最大值、最小值及相應的可變單元(決策變量)值,規劃求解工具具有數據輸入直觀、簡單、計算快捷,并可生成完整的求解報告等特點。
4 結論及建議
水資源規劃目的是根據經濟社會可持續發展和環境保護對水資源的要求,提出水資源合理開發、優化配置、高效利用、有效保護和綜合治理的總體布局及實施方案,促進我國人口、資源、環境和經濟的協調發展,以水資源的可持續利用支持經濟社會的可持續發展。
水資源規劃是全面落實國家或地區實施可持續發展戰略的要求,適應經濟社會發展和水資源的時空動態變化,著力緩解水資源短缺、水環境惡化等水問題的一項重要工作。它是根據國家或地區的社會、經濟、資源和環境總體發展規劃,以區域水文特征及水資源狀況為基礎來進行的。
通過對線性規劃的介紹與實例分析,線性規劃的建模過程簡單,首先是明確模型的目標函數和約束方程,然后根據線性規劃解的求解方法和過程,很容易得到模型的全局最優解。從結果可以看出,在滿足供水要求的前提下,供水效益最大,從而為水資源的合理配置提供了理論依據和基礎。但在生產實踐中,目標函數與約束條件往往不是決策變量的線性函數,為了解決生產實際中的問題,往往還需要用到非線性規劃法、動態規劃法以及人工神經網絡的應用,滿足水資源優化配置的更高要求。

