降落傘和尾翼相結合的末敏彈布局形式

高偉濤,崔占忠,李永遠,鄭 堅

(1.北京理工大學機電學院,北京 100081;2.二炮裝備研究院,北京 100085)

0 引言

穩態掃描技術是末敏彈系統研制過程中的關鍵技術之一。目前,使子彈形成穩態掃描運動主要有兩種技術方案:一是采用降落傘,二是采用氣動力機構。由于本文所研究末敏彈的質量大,若采用降落傘布局形式,則所需的降落傘體積大,目標明顯,系統易受到敵方的反擊;若采用單翼或雙翼布局,又受到阻力大小的限制。故在結構上采用了降落傘和尾翼相結合的布局形式。

1 末敏彈氣動布局

末敏彈的氣動布局主要根據其有無穩態掃描過程而分為兩大類:一類為沒有減速減旋裝置的末敏彈,其主要代表有美國研制的GBU-97/B中的SKEET(斯基特)和X93式“大黃蜂”反坦克地雷、法國的ACDE等;而另一類則為有形成穩態掃描運動的減速減旋裝置,其主要代表有美國的SADARM、德國的SMArt155和俄羅斯的RBK-500式SPBE反坦克子母炸彈。

目前,使子彈形成穩態掃描運動主要有兩種技術方案[1]:一是采用降落傘,包括減速減旋降落傘和渦旋降落傘,通常稱為有傘掃描,這種方式的優點是子彈下降和旋轉的速度較慢,對敏感器件的反應速度要求不是很高,電子部件實現容易,缺點是降落傘體積大,易受敵方的反擊,且系統受風的影響也較大;二是采用氣動力機構,即采用雙翼或單翼來形成所需的掃描運動,其缺點是翼片阻力面的大小受圓柱形子彈體橫截面大小的限制,如果因戰斗部的重量增大而需要增大阻力時,就會出現問題。

以上兩類布局方式各有優缺點,針對二者的優缺點,本文提出了一種降落傘和尾翼相結合的布局形式。

2 傘翼結合的布局形式

2.1 傘翼布局原理

傘翼布局采用的是降落傘和尾翼相結合的布局形式,在子彈的尾部安裝了三片弧形尾翼,在尾翼的上方懸掛有降落傘,其示意圖如圖1所示。

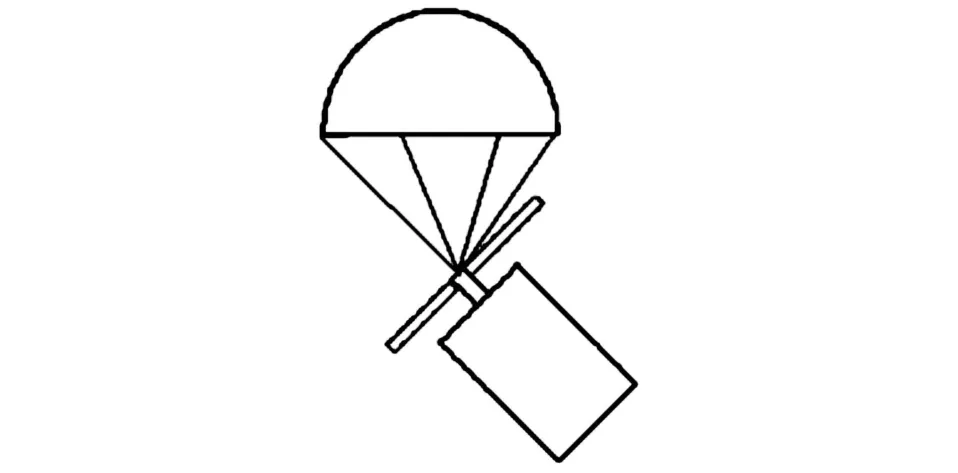
圖1 傘翼布局示意圖Fig.1 The sketch map of parachute-wing configuration

采用傘翼布局時,整個傘彈系統的氣動參數由兩部分組成,一部分為降落傘的氣動參數,另一部分為子彈的氣動參數。

2.2 傘翼布局的數學模型

為獲得子彈氣動參數,對翼展開后的末敏彈進行了數值風洞模擬。數值風洞模擬所建立基本守恒方程組為一般流體力學所具有的質量守恒方程(即連續方程)、動量守恒方程、能量守恒方程,并且在能量守恒方程中需要考慮熱量傳遞。在這些守恒方程的基礎上,加上必要的輔助方程就構成了控制方程。

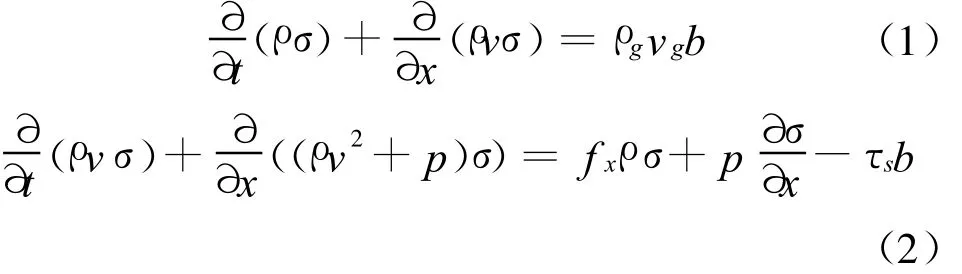
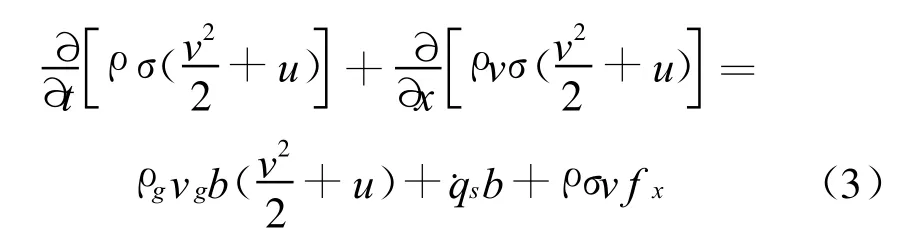
在對子彈進行氣動仿真時,忽略了降落傘對子彈氣動力計算的干擾。由于整個傘-彈系統降落的速度較小,遠場的仿真域為圓柱體,軸向為20倍彈長,徑向為10倍彈徑,并對子彈網格進行了加密,建立的計算模型網格圖如圖2所示。

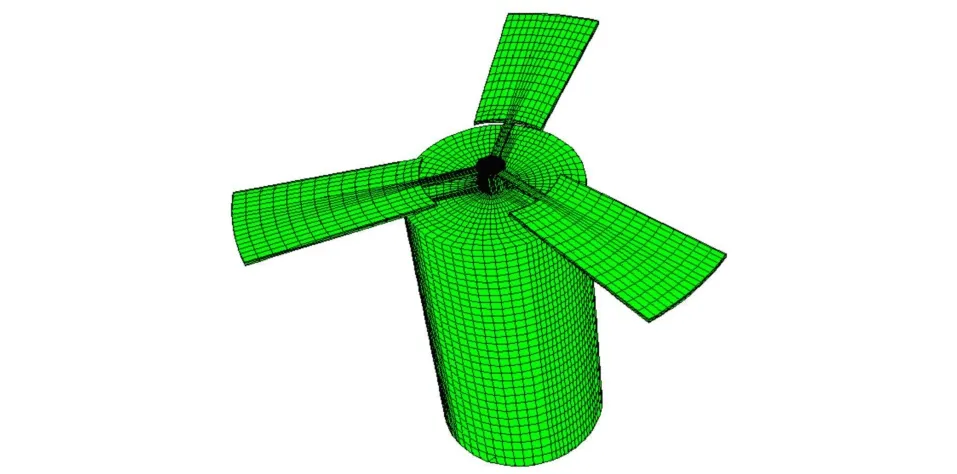
圖2 計算網格模型Fig.2 Calculation mesh model

2.3 子彈氣動仿真結果分析

根據計算流體動力學(CFD)理論,在Gambit和FLUENT軟件平臺上對計算模型進行了仿真,通過數值模擬方法研究子彈在自旋情況下的繞流流場特性以及子彈的氣動參數計算。在末敏彈豎直下落時,尾翼的上部處于小負壓區域,而子彈頭部和三個尾翼下部壓力相對別的部位來說比較大,最大為0.27個表壓,因而受到的升力比較大,其他方向的力和力矩都比較小。子彈豎直下落即攻角為0°時的壓力云圖如圖3所示。

圖3 0°攻角子彈頭和尾翼下部壓力云圖Fig.3 0°Attack angle the head of projectile and the lower-part of empennage＇s pressure nephogram

通過仿真計算可以得出,在馬赫數為0.6時,由于尾翼的迎風面增大的緣故,隨著攻角增大,阻力系數變化呈線性變化。在攻角增加到60°以后,阻力系數變化較緩,其變化趨勢如圖4所示。

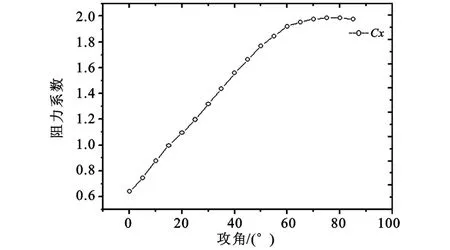
圖4 阻力系數隨攻角變化Fig.4 Resistance coefficient change with the attack angle

升力系數在攻角為28°時達到最大,約為2.2,其后升力系數開始減小,其變化趨勢如圖5所示。

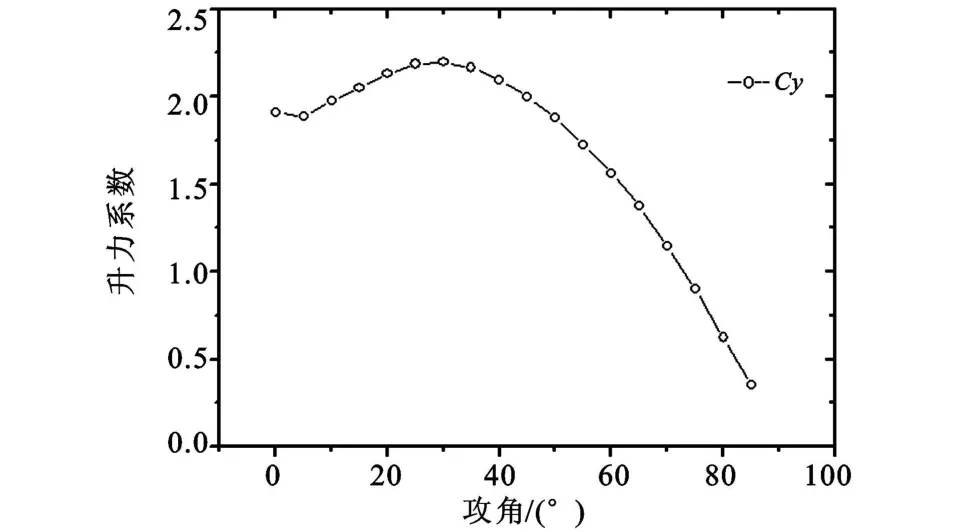
圖5 升力系數隨攻角變化Fig.5 Lift coefficient change with the attack angle

本文氣動仿真結果與試驗結果吻合得很好。在攻角為30°,即掃描角為30°時,氣動仿真計算的結果為1.319,試驗的結果為1.301。氣動仿真的結果為末敏彈的穩態掃描彈道仿真提供了可靠的參數。

3 雙歐法六自由度方程組求解

在求解末敏彈飛行彈道時,為了克服子彈全方位六自由度解的奇異性問題,也就是三角函數在某些點趨于無窮值的問題,采用雙歐拉法求解。子彈的姿態可以用3個歐拉角來確定,在航空領域廣泛采用的是偏航角ψ、俯仰角?和滾轉角γ。求解歐拉角的歐拉方程具有奇異性,即:它有一對奇異點,使得在趨近奇異點的區域內產生解算誤差,而在奇異點上無法解算[2-4]。

按照飛行力學的概念,地面坐標系變換到體軸系時,需要依次變換三次,如果變換順序是按偏航、俯仰和滾轉,則對應的偏航角、俯仰角和滾轉角等為正歐拉角,分別記做 ?、ψ、γ,其角速度與子彈的轉角速度 ωx1、ωy1、ωz1的關系如式(4)中所示,式(4)就是正歐拉方程組

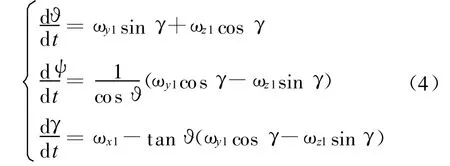
?=±90°為此方程組的奇異點;而在?=0°或?=±180°附近時,方程解的精度將提高,在這里稱此求解范圍為正歐拉方程解的精華區;故在小俯仰角情況下,采用正歐拉方程求解可得到較理想的結果。但是對于某些俯仰角變化較大的系統,僅用正歐拉方程就難以求解了。

如果變換轉動次序,按照俯仰、偏航和滾轉,稱此套歐拉角為“反歐拉角”,并用下標r表示。相應的歐拉運動學方程如式(5)中所示。

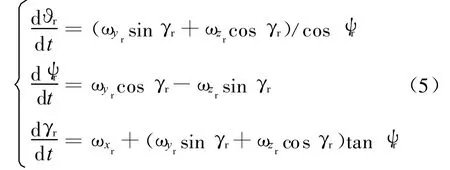
單就反歐拉方程來說,同樣也存在著奇異性問題,即當ψr=±90°為此方程組的奇異點;而在ψr=0°或 ψr=±180°附近時,方程解的精度將提高,在這里稱此求解范圍為反歐拉方程解的精華區。

通過上面的分析可知正、反歐拉方程都存在奇異性的問題。但兩者的精華區和奇異區卻不盡相同,若能綜合考慮,則可避免在正、反歐拉方程的奇異區內求解,從而達到克服歐拉方程奇異性的目的。

由式(5)可以看出,反歐拉方程精華區在?r=±90°附近,其奇異區在 ?r=0°或 ?r=±180°附近。這一點正好與正歐拉方程相反。如果以±45°或±135°為界將0°～360°的區域劃分為如圖 6所示的形式,利用正、反歐拉方程之間精華區和奇異區的倒掛關系,就可以避免求解過程中奇異性的出現,同時還可提高解的精度。

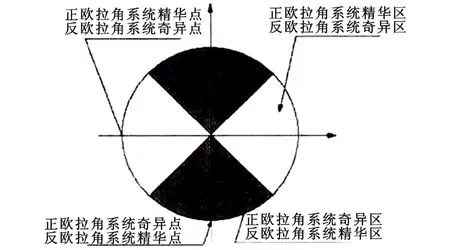
圖6 正反歐拉方程精華區與奇異區Fig.6 The essence area and singular area of positive-negative euler equation

4 彈道仿真結果分析

把仿真所獲得的氣動參數代入傘彈系統的運動微分方程組中,運用雙歐拉法求解該變系數的微分方程組。仿真結果如圖7～圖10所示。

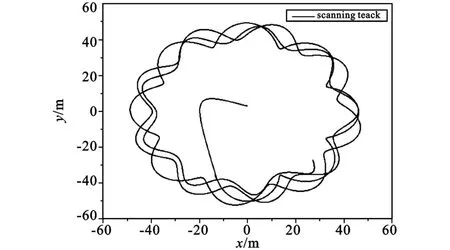
圖7 末敏彈0～5 s掃描軌跡線Fig.7 The 0～ 5 seconds＇scanning track of terminal-sensitive projectiles

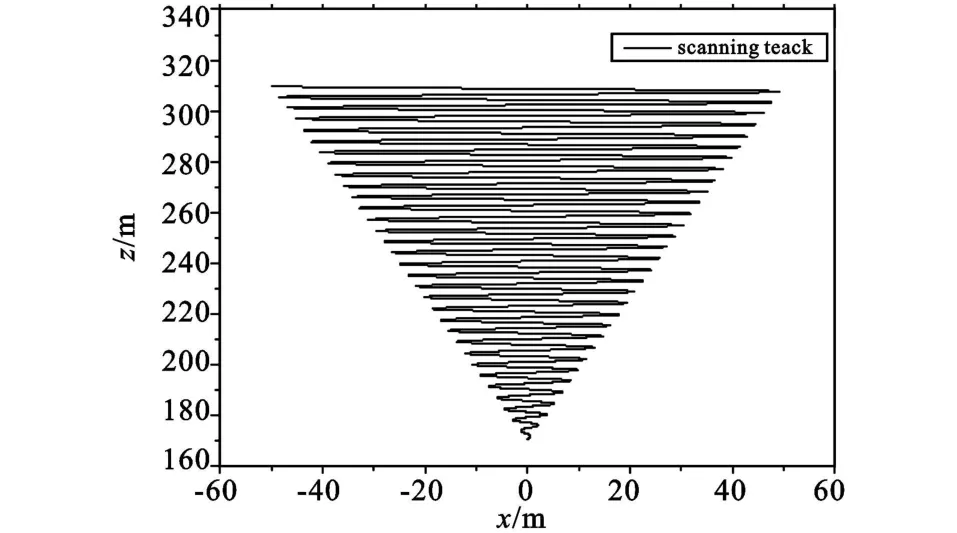
圖9 末敏彈20～40 s鉛垂平面掃描軌跡線Fig.9 The 20 ～ 40 seconds＇scanning track on plumb plane of terminal-sensitive projectiles plumb plane

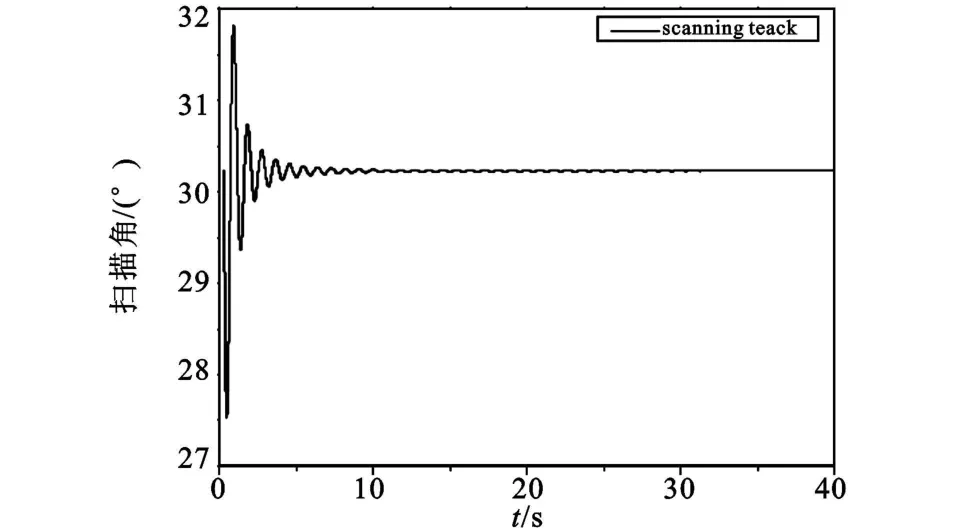
圖10 末敏彈掃描角變化Fig.10 Scanning angle of terminal-sensitive projectiles changewith time

由圖7可以看出,該傘彈系統的穩態掃描時間穩定得較好,0～5 s時的掃描曲線看上去雖然仍很紊亂,但已有趨于穩定的趨勢。

由圖8可以看出,在20～30 s,傘彈系統已經完全進入了穩態的掃描階段,掃描曲線為等間距的螺紋線,并可直接從圖上讀出該掃描間距為1.48 m。

圖9為末敏彈在鉛垂平面上的掃描軌跡,此掃描軌跡線看上去類似一個等腰三角形,如果從空間上看去,則該掃描軌跡線為一圓錐體。如果以20 s時進入穩態掃描階段。則由圖9可以看出,該末敏彈的掃描面積約為7 850 m2。

由圖10可以看出,大約在5 s時子彈的掃描角便已趨于穩定。

5 結論

本文針對末敏彈在采用降落傘和其他氣動力機構(采用單翼或雙翼)穩態掃描時的缺點,提出了一種降落傘和尾翼相結合的布局形式。這種布局形式通過在子彈尾部安裝三片尾翼,可在穩態掃描時為子彈提供一定的阻力,減小攜帶降落傘的尺寸,提高了末敏彈的作戰效果。通過對子彈進行氣動仿真和彈道分析,表明該布局形式的可行性,可用于下一步的末敏彈武器系統研制中。

[1]楊啟仁,耿茂盛.子母彈拋撒動力學模型[C]//中國兵工學會彈道學術交流論文集.廈門:中國兵工學會彈道專業委員會,1992:498-502.

[2]陳廷楠,張登成.雙歐法與四元數法的應用比較[J].飛行力學,1996(12):59-64.CHEN Tingnan,ZHANG Dengcheng.Application comparision of dual Euler method and quaternion method[J].Flight Dynamics,1996(12):59-64.

[3]黃雪樵.克服歐拉方程奇異性的雙歐法[J].飛行力學,1994(12):28-37.HUANG Xueqiao.The Dual Euler method for Overcoming the Singularity of Euler Equation[J].Flight Dynamics,1994(12):28-37.

[4]周偉,張曉今,寇保華.雙歐法在克服傘-彈系統歐拉方程奇異性中的應用[J].航天返回與遙感,2003(9):4-8.ZHOU Wei,ZHANG Xiaojin,KOU Baohua.The application of the dual-euler method for overcoming the singularity of euler equation in parachute-missile system[J].Spacecraf t Recovery&Remote Sensing,2003(9):4-8.