簡析函數對稱性和周期性的關系

●周少鋒 (嵊州市第一中學 浙江嵊州 312400)

函數內容貫穿于高中數學的始終，歷來是高考考查的難點和熱點，要求學生熟練掌握函數的性質.但在學習過程中，許多學生都被函數的若干性質弄得頭昏腦漲.事實上，只要把握好其中的關系，就不難解決了.函數的這些性質到底有哪些相互關系呢?這里就以函數圖像的對稱性和周期性為例，探討它們之間的關系.

在學習三角函數知識時，我們知道三角函數是周期函數，它的變化過程是周期性不斷重復的.以下2條性質已是人所共知的函數性質，在研究函數圖像的對稱性和周期性時，若以三角函數為例，則更容易理解.

性質1 若函數f(x)滿足f(a+x)=f(a-x)(或f(2a-x)=f(x))，x∈D(D是函數f(x)的定義域)，則函數f(x)的圖像關于直線x=a對稱.

性質2 若函數f(x)滿足f(a+x)=-f(ax)(或f(2a-x)=-f(x))，x∈D(D是函數f(x)的定義域)，則函數f(x)的圖像關于點(a，0)對稱.

對于這2條性質與函數周期性的關系，討論得不多.本文試圖就這2個方面作一些探索，求教于同行.

1 由函數的對稱性討論周期性

定理1 若函數f(x)的圖像關于直線x=a對稱，且f(x)的圖像又關于直線x=b對稱(a≠b)，則函數f(x)是一個周期函數，且周期T=2k(ba)(k∈Z，k≠0).

證明因為f(x)的圖像關于直線x=a對稱，且關于直線x=b對稱(a≠b)，所以對于任意t∈R，有

令 2b-t=x，則

代入式(1)得

又由 a≠b，得

因此f(x)的周期是 T=2k(b-a)(k∈Z，k≠0).

例1 設函數f(x)在(-∞，+∞)上滿足

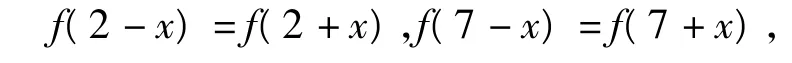
且在閉區間［0，7］上，只有 f(1)=f(3)=0.

(1)試判斷函數y=f(x)的奇偶性;

(2)試求方程f(x)=0在閉區間［-2 005，2 005］上的根的個數，并證明你的結論.

(2005年廣東省數學高考理科試題)

分析(1)由 f(2-x)=f(2+x)，f(7-x)=f(7+x)，知函數f(x)關于直線x=2和x=7對稱.從而由定理1知函數y=f(x)是周期函數，且周期為 T=2k(7-2)=10k.又

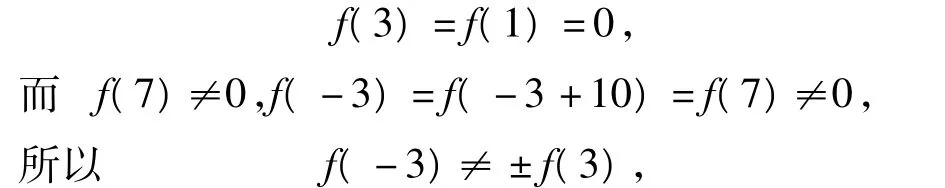
故函數y=f(x)是非奇非偶函數.

(2)又 f(3)=f(1)=0，f(11)=f(13)=f(-7)=f(-9)=0，故 f(x)在［0，10］和［-10，0］上均有2個解，從而可知函數y=f(x)在［0，2 005］上有402個解，在［-2 005，0］上有400個解，所以函數y=f(x)在［-2 005，2 005］上有802個解.

定理2 若函數f(x)的圖像關于點A(a，0)對稱，且f(x)的圖像又關于點 B(b，0)對稱(a≠b)，則函數f(x)是一個周期函數，且周期T=2k(ba)(k∈Z，k≠0).

證明f(x)的圖像關于點 A(a，0)和 B(b，0)都對稱，故對于任意t∈R，有

令 x=2b-t，則

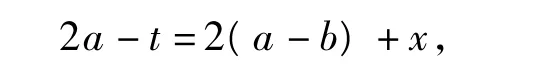
代入式(2)得

又由 a≠b，得從而f(x)是以T=2k(b-a)(k∈Z，k≠0)為周期的周期函數.

例2 函數f(x)的定義域為R，若f(x+1)與f(x-1)都是奇函數，則 ( )

A.f(x)是偶函數 B.f(x)是奇函數

C.f(x)=f(x+2) D.f(x+3)是奇函數

(2009年全國數學高考理科試題Ⅰ)

分析由f(x+1)是奇函數，可知f(x)關于點(1，0)對稱;由f(x-1)是奇函數，可知f(x)關于點(-1，0)對稱.又由定理2知，f(x)是一個周期函數，且周期

故選D.

例3 已知f(x)是R上的偶函數，g(x)是R上的奇函數，且g(x)=f(x-1)，若f(-2)=a(a為常數)，則f(2 002)= _______.

分析由已知得

故f(x)關于點(1，0)對稱.因為f(x)是偶函數，所以f(x)也關于點(-1，0)對稱.由定理2知，f(x)是一個周期函數，且周期

定理3 若函數f(x)的圖像關于直線x=a對稱，且f(x)的圖像又關于點(b，0)對稱(a≠b)，則函數f(x)是一個周期函數，且周期T=4k(b-a)(k∈Z，k≠0).

證明由函數f(x)的圖像關于直線x=a對稱，且f(x)的圖像又關于點(b，0)對稱(a≠b)，得

因此f(x)是以T=4k(b-a)(k∈Z，k≠0)為周期的周期函數.

A.-2 B.-1 C.0 D.1

(2010年浙江省紹興市統考試題)

得f(x)是偶函數.由定理3知，函數f(x)是周期函數，且周期為

2 由函數的周期性討論對稱性

證明由函數f(x)的圖像關于直線x=a對稱，且f(x)是周期為T的周期函數，得

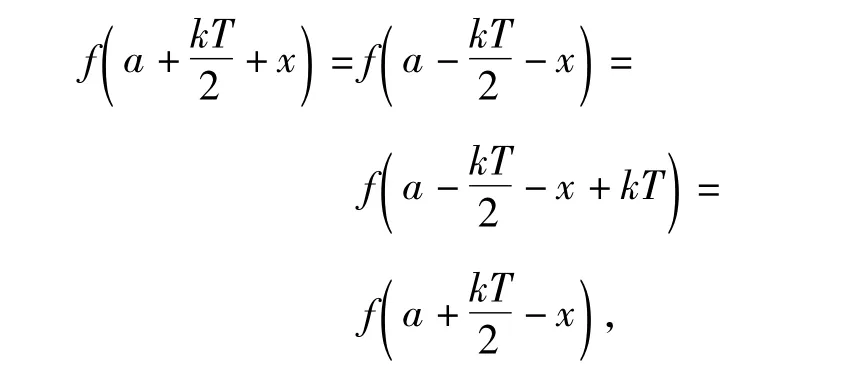
例5 已知定義在R上的奇函數 f(x)滿足f(x-4)=-f(x)，且在區間［0，2］上是增函數.若方程f(x)=m(m＞0)在區間［-8，8］上有4 個不同的根 x1，x2，x3，x4，則x1+x2+x3+x4= _______.

圖1

(2009年山東省數學高考理科試題)

分析因為定義在R上的奇函數滿足f(x-4)=-f(x)，所以

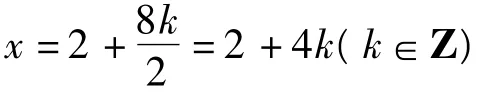
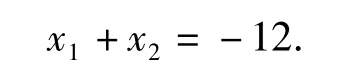
由點x3，x4關于直線x=2對稱，得

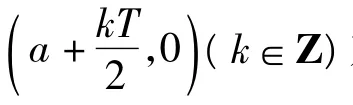
證明函數f(x)的圖像關于點(a，0)對稱，且f(x)是周期為T的周期函數，從而

例6 定義在R上的函數f(x)既是奇函數，又是周期函數，3是它的一個正周期.若將方程f(x)=0在閉區間(0，6)上的根的個數記為n，則n可能為 ( )

A.0 B.1 C.3 D.5

(2007年安徽省數學高考理科試題)

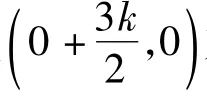
但以下2個命題卻不一定成立.

反例：f(x)=|tanx|只有對稱軸，但沒有對稱中心.

反例：f(x)=tanx只有對稱中心，沒有對稱軸.

注若已經知道函數f(x)既有對稱中心，也有對稱軸，則以上2個命題均成立.

綜上可知，認識函數對稱性和周期性可使我們對函數的圖像特征與性質有比較清晰的認識，克服對函數(特別是抽象函數)恐懼的心理，從而進一步引導學生解題思想方法的探求，提高解決問題的能力，培養思維的靈活性，最終達到培養創新思維的目標.

［1］ 王國云.抽象函數的對稱性與周期性芻議［J］.中學教研，2010(6)：31-33.

［2］ 侯立剛.例析函數中十二對易混問題［J］.數理化解題研究，2009(1)：1.

［3］ 張建國.函數圖像的對稱性與其周期的教學［J］.上海中學數學，2009(6)：14.