調和擬共形映照雙曲雅可比的偏差性質

陳行堤

（華僑大學數學科學學院，福建 泉州 362021）

調和擬共形映照雙曲雅可比的偏差性質

陳行堤

（華僑大學數學科學學院，福建 泉州 362021）

研究兩類調和擬共形映照雙曲雅可比和雙曲面積的偏差性質，給出上半平面到自身上的歐氏調和擬共形映照雙曲雅可比的精確界限，以及達到極值的函數.研究雙曲調和擬共形映照雙曲雅可比的偏差估計，并應用于兩類調和擬共形映照雙曲面積的偏差估計.結果表明，這兩類調和擬共形照是非爆破的.

調和映照；擬共形映照；雙曲雅可比；雙曲面積

1 基本概念

一個上半平面H到自身上的C2同胚映照f，被稱為ρ-調和映照.若它滿足Euler-Lagrange方程，即

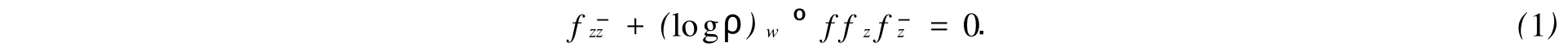
式（1）中：ρ是一個H上的C2正值函數；w=f（z）.一個H到自身上的保向同胚映照f，被稱為K-擬共形映照.它滿足：（1）f在H上是ACL的；（2）對幾乎所有的z∈H，滿足Beltrami方程.即

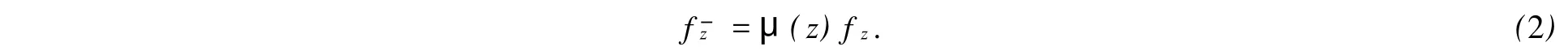
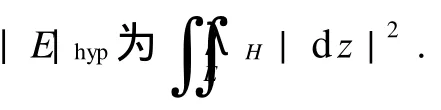
一個局部單葉解析函數的歐氏雅可比總是正的［1］.Lewy［2］證明了對于一個局部單葉的保向歐氏調和映照.這個結論是正確的，但對一個擬共形映照就未必成立.如取f=z|z|4，則f是單位圓盤到自身上的擬共形映照，其歐氏雅可比在0點處為零.Partyka等［3］研究了在歐氏度量意義下，歐氏調和K-擬共形映照能量密度的偏差性質，結果隱含著如下定理.

定理1給定K≥1，如果f是單位圓盤D到自身上的歐氏調和K-擬共形映照，且滿足f（0）=0，那么有

其中：LK關于K≥1是嚴格遞減函數，且滿足

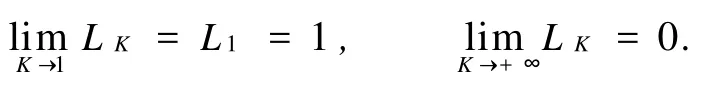
研究了上半平面到自身上的歐氏調和K-擬共形映照類，證明了其雙曲雅可比的精確的上界和下界分別為K和1/K；證明上半平面到自身上的雙曲調和K-擬共形映照類；證明其雙曲雅可比的上界和下界估計分別為（K+1）2/4，4K/（K+1）2.容易看出，當K＞1時，有（K+1）2/4K＜K，4K/（K+1）2＞1/K.

在歐氏度量意義下，Astala［4］和Chen等［5］給出了擬共形映照的面積偏差的精確估計.在雙曲度量意義下，Kelingos［6］首先研究了有界可測子集的情形.Porter等［7］構造例子，用于說明存在擬共形映照，使得雙曲面積有限的可測子集在其映照下的像具有無限的雙曲面積.因此，對一般可測子集的雙曲面積的研究，由于存在爆破現象而比較復雜.目前，對非爆破的擬共形映照類的已有相關的研究結果［7-10］.

2 主要結果及其證明

記上半平面H的雙曲度量為λH（z）|dz|2，則在Gauss曲率標準化為-1的條件下，有

為了方便，記AK（z）=（c/K）x+icy+b，BK（z）=c Kx+icy+b.其中：b，c是兩個實常數，且c＞0.

引理1［11］如果f=u+iv為一個上半平面H到自身上的歐氏調和擬共形映照，并且滿足標準化條件f（∞）=∞.那么，v=cy，c是一個正常數.

利用上述的引理1，有

定理2 如果f是一個上半平面H到自身上的歐氏調和K-擬共形映照，那么，不等式

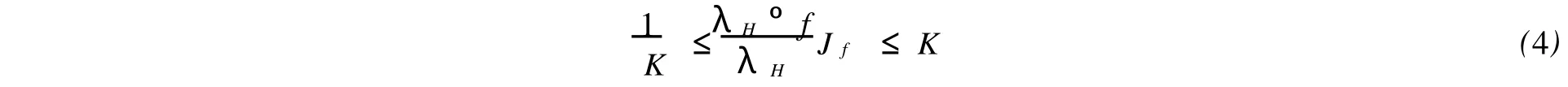
對每個z∈H成立.當且僅當f=AK°L，左邊等號成立；當且僅當f=BK°L，右邊等號成立.這里，L是一個H到自身上滿足L-1（∞）=f-1（∞）的共形映照.

證明 假設f（z）=u（x，y）+iv（x，y）是一個上半平面H到自身上的歐氏調和K-擬共形映照，且滿足標準化條件f（∞）=-∞，z=x+iy.由引理1可知，存在一個正常數c，使得f（z）=u（x，y）+icy，從而有

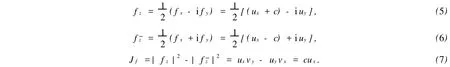
因為f是K-擬共形的，所以由式（5），（6）可得

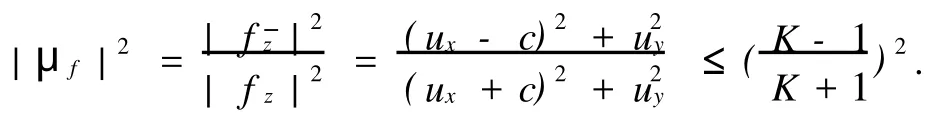
經整理，可得

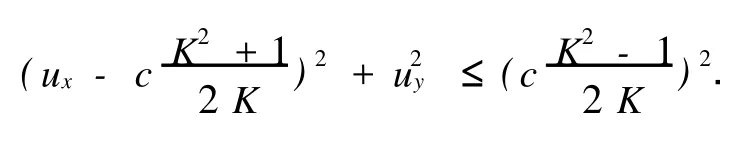
它隱含著

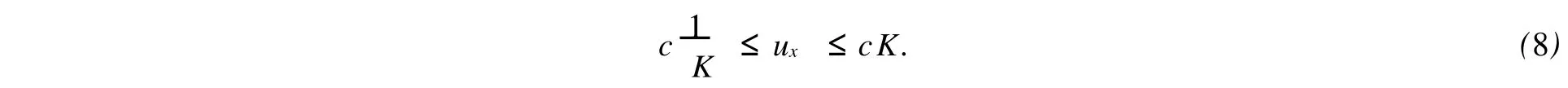
根據式（3）和Imf=cy，有

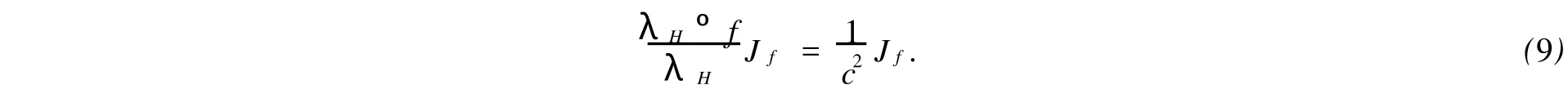
由式（7），（8），（9）可得

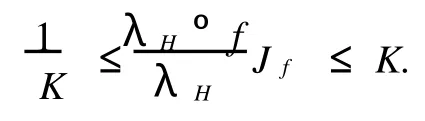
假設左邊不等式的等號成立，則有ux=c/K.因此，存在著一個函數φ（y），滿足u（x，y）=（c/K）x+φ（y）.由于f是H上的歐氏調和映照，可知

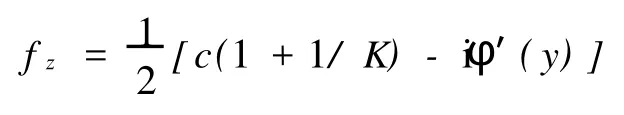
在H上是解析的.因此，φ′（y）是一個實常數，記其為d.由式（5），（6）有

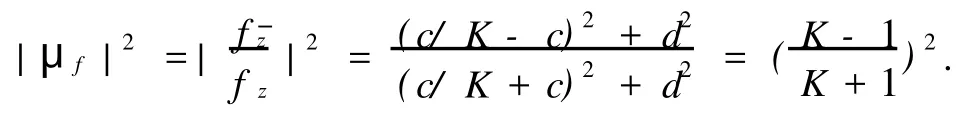
上面等式只有在d=0的情形下成立，從而φ（y）是一個實常數，記為b.當f滿足標準化條件f（∞）=∞時，不等式（4）的左邊等號當且僅當f=AK時成立.同理可證明，當f滿足標準化條件f（∞）=∞時，不等式（4）的右邊等號當且僅當f=BK時成立.

如果f（∞）≠∞，則存在實軸上的一點a，滿足f（a）=∞，讓L為一個H到自身上滿足L（a）=∞的共形映照.

令g=f°L-1，則g是一個H到自身上的歐氏調和K-擬共形映照且滿足標準化條件g（∞）=∞.從而有

1/K≤（λH（w）/λH（ζ））Jg≤K.

上式中：w=f（z）；ζ=L（z）.由于L是一個H到自身上的共形映照，所以有

λH（L（z））|L′（z）|2=λH（z）.

根據Jg=Lf°L-1|（L-1）′（ζ）|2，有

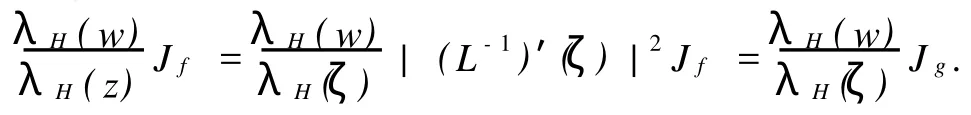
因此，有

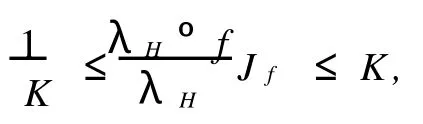
左邊的等號當且僅當f=AK°L成立，而右邊的等號當且僅當f=BK°L成立.定理2證畢.

推論1 若f是一個上半平面H到自身上的歐氏調和K-擬共形映照，且滿足f（∞）=∞和f（i）=i，那么有

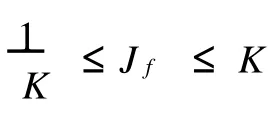
對每個z∈H成立.左邊等號成立當且僅當f=（1/K）x+iy，而右邊等號成立當且僅當f=Kx+iy.

下面考慮雙曲調和K-擬共形映照的雙曲雅可比的偏差估計.即

引理2［12］如果σ＞0是一個上半平面H上的C2度量密度函數，且其Gauss曲率滿足Kσ≤-1，則σ≤λH.

定理3［13］如果f是一個上半平面H到自身上的雙曲調和K-擬共形映照，那么有

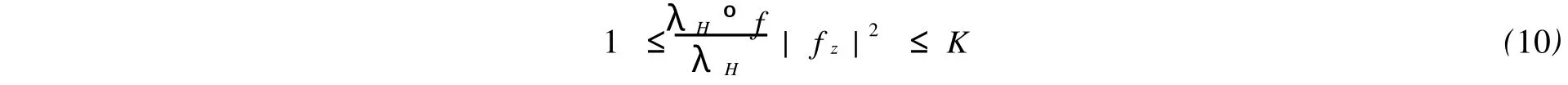
對每個z∈H成立.利用引理2和定理2可得

定理4 如果f是一個上半平面H到自身上的雙曲調和K-擬共形映照，那么不等式

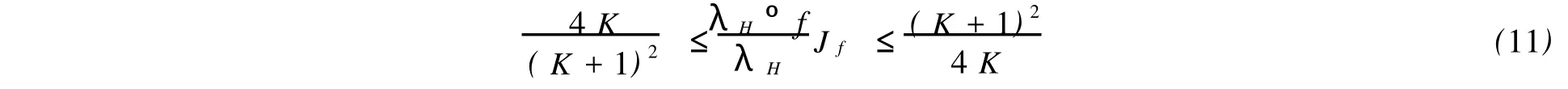
對每個z∈H成立.

證明 令σ=（1-k2）λH°f|fz|2，k=（K-1）/（K+1）.由定理2可知，對于任意z∈H，都有|fz|≠0；而對于滿足|f|≠0的點z∈H，有

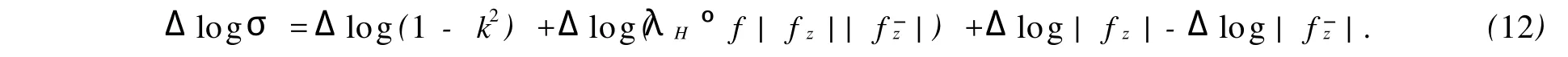
因為f是雙曲調和的，所以λH°ffzz是一個H上的解析函數.從而有

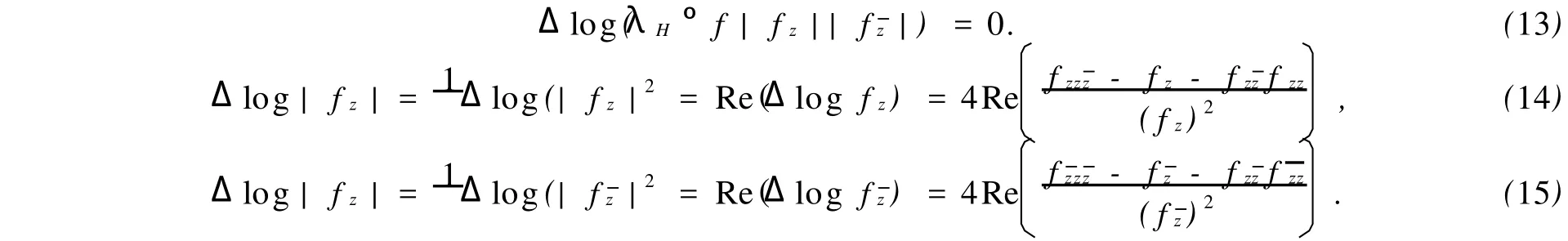
根據f=-（logλH）w°ffzf，可得

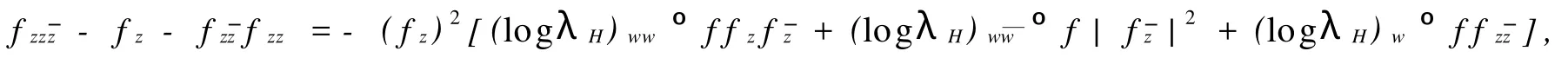
將以上兩個等式分別代入關系式（14），（15），則有

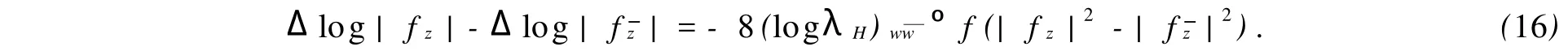
因此，當|f|≠0時，將式（13），（16）代入式（12），可得

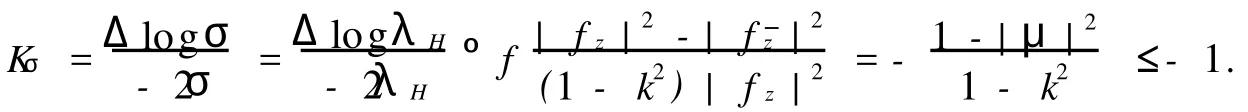
另外，Δlogσ也可表示為

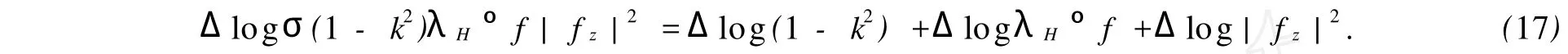
由式（3）可得，（logλH）zz=-（1/2）λH成立.利用這個等式，可得

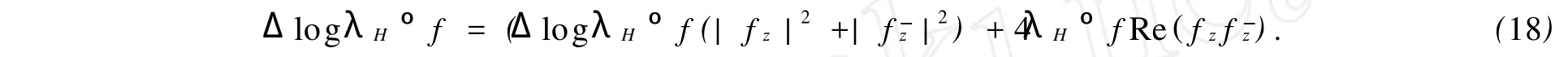
又有

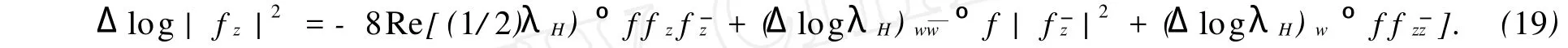
Δlog（1-k2）λH°f|fz|2=（ΔlogλH）°f|fz|2；

而式（17）在滿足|f|=0的點處，有

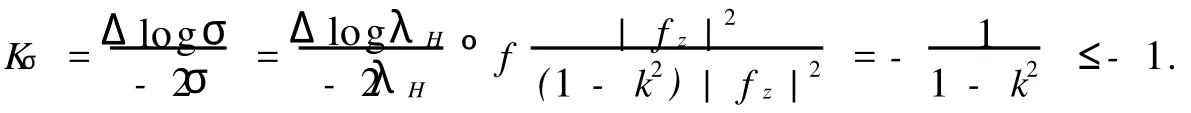
因此，對于任意的z∈H，都有Kσ≤-1.

由引理3，有

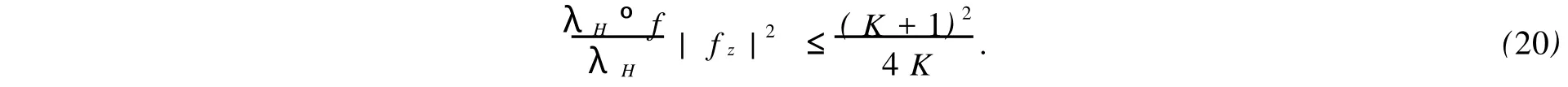
結合定理3的左邊不等式和關系式，由Jf≥（1-k2）|fz|2可知，式（11）的左邊不等式對任意的z∈H也成立.

利用雙曲調和擬共形映照的共形不變性［5］，定理3對任意的單連通區域結論都成立.Yao［14］改進了定理3的右邊不等式為

（λH°f/λH）|fz|2≤（K+1）/2，

而式（20）改進了文［14］的結果.從定理4可看出，H上的雙曲調和擬共形映照雙曲雅可比的偏差比歐氏調和擬共形映照的要小.

3 主要結果的應用

定理5 如果f是一個上半平面H到自身上的歐氏調和K-擬共形映照，那么，對于任意的可測集合E?H，有

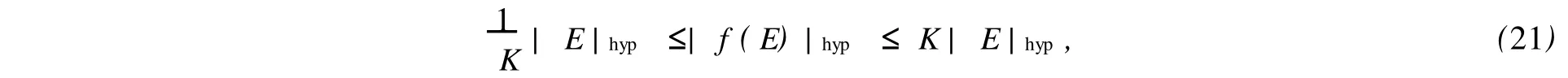
而且，其上界和下界的估計是精確的.

證明 設f是一個上半平面H到自身上的歐氏調和K-擬共形映照，則由定理2有

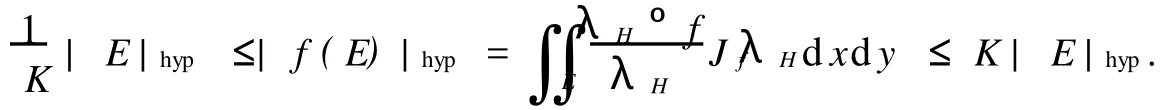
如果f（z）=Kx+iy，z=x+iy，則對任意的可測集合E?H，有（λH°f/λH）Jf≡K，從而有

|f（E）|hyp= K|E|hyp，

即式（21）的右邊不等式是精確的.類似地，若取f（z）=（1/K）z+iy，則可證明式（21）的左邊不等式也是精確的.定理5證畢.

由定理4可得

定理6 如果f是一個上半平面H到自身上的雙曲調和K-擬共形映照，那么，對于任意的可測集合E?H，有

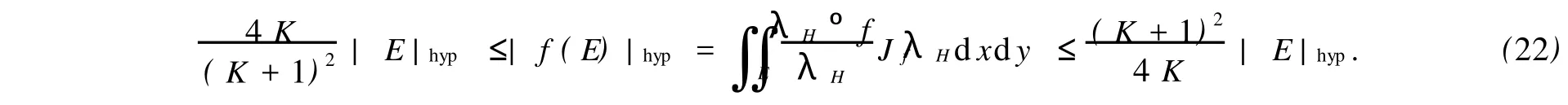
［1］AHLFORS L V.Complex analysis［M］.3rd ed.New York：McGraw-Hill Book Company，1979.

［2］L EWY H.On the non-vanishing of the Jacobian in certain one to one mapings［J］.Bull Amer Math Soc，1936，42（10）：689-692.

［3］PARTYKA D，SAKAN K I.On an asymptotically sharp variant of Heinz’s inequality［J］.Ann Acad Sci Fenn Ser AI，2005，30（1）：167-182.

［4］ASTALA K.Area distortion of quasiconformal mappings［J］.Acta Math，1994，173（1）：37-60.

［5］CHEN Xing-di，FANG Ainong.Harmonic Teichmüller mappings［J］.Proc Japan Acad Ser（A）：Math Sci，2006，82（7）：101-105.

［6］KELINGOS J A.Distortion of hyperbolic area under quasiconformal mappings［J］.Duke Math J，1974，41（1）：127-139.

［7］PORTER R M，RESéNDIS L F.Quasiconformally explodable sets［J］.Complex Variables，1998，36（4）：379-392.

［8］陳行堤，黃心中.擬共形映照的爆破集問題［J］.華僑大學學報：自然科學版，2001，22（2）：111-116.

［9］CHEN Xing-di，HUANG Xin-zhong.On the estimates of hyperbolic area distortion of quasiconformal mappings［J］. Chinese Quart J Math，2007，22（1）：137-142.

［10］韓雪，黃心中.擬共形映照的雙曲面積偏差［J］.華僑大學學報：自然科學版，2007，28（4）：433-436.

［11］KALAJ D，PAVLOVIC M.Boundary correspondence under quasiconformal harmonic diffeomorphisms of a halfplane［J］.Ann Acad Sci Fen Math，2005，30（1）：159-165.

［12］AHLFORS L V.Conformal invariants：Topics in geometric function theory［M］.New York：McGraw-Hill Book Company，1973.

［13］WAN T.Constant mean curvature surface，harmonic maps and universal Teichmüller space［J］.J Differential Geom，1992，35（3）：643-657.

［14］YAO Guo-wu.Convergence of harmonic maps on the Poincarédisk［J］.Proc Amer Math Soc，2004，132（8）：2483-2493.

Distortion Estimations of the Hyperbolic Jacobians of Harmonic Quasiconformal Mappings

CHEN Xing-di
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

The distortion estimation with respect to the hyperbolic metrics of two classes of harmonic quasiconformal mappings is studied.First，the sharp upper and lower bounds of the hyperbolic Jacobians of Euclidean harmonic quasiconformal mappings from the upper half-plane onto itself and their corresponding extremal functions are given.Secondly，the distortion estimation of hyperbolic Jacobian of hyperbolic quasiconformal mappings are obtained.Finally，the distortion estimation of the above two classes of mappings is applied to study their corresponding distortion theorems about hyperbolic areas.The results show that the above two classes of harmonic quasiconformal mappings are non-explodable.

harmonic mappings；quasiconformal mappings；hyperbolic Jacobians；hyperbolic areas

O 174.55

A

1000-5013（2010）03-0351-05

（責任編輯：陳志賢 英文審校：張金順，黃心中）

2008-10-03

陳行堤（1976-），男，講師，主要從事函數論的研究.E-mail：chxtt@hqu.edu.cn.

福建省自然科學基金資助項目（S0650019）；華僑大學高層次人才科研啟動項目（08BS107）