旋轉機械故障診斷中的改進型RBF神經網絡算法研究

張忠奎,王效岳,丁曉坤

(1.山東理工大學機械工程學院,山東 淄博 255049;2.聊城大學計算機科學學院,山東 聊城 252059)

旋轉機械是石油、化工、冶金、機械等行業生產中的關鍵設備,隨著其大型化、自動化、高速化和復雜化發展,運行的可靠性和安全性日益受到重視.因此,對其進行可靠、準確的故障診斷具有十分重要的意義.但是旋轉機械結構的復雜性和耦合性又使得其故障具有多樣性、模糊性和隨機性等特點,因此很難用傳統的模式分類技術將這些故障截然分開.而人工神經網絡具有非線性模式分類性能和很強的自組織、自學習能力[1],不需要預先給出關于模式的先驗知識和判別模型就能夠通過自組織和自學習機制自動地形成所要求的決策域;同時,由于網絡內部的非線性傳遞函數,使其對高維空間及非線性空間數據模式具有較強的分類能力,非常適用于設備的故障診斷.機械故障診斷中,常來用較為成熟的BP神經網絡,但在實際的應用中,BP網絡采用的是沿梯度下降的搜索求解算法,這就不可避免地存在網絡學習收斂速度慢、易陷入局部極小、網絡初值對學習性能影響比較大等缺陷[2].本文提出一種基于改進型RBF網絡的旋轉機械故障診斷方法,通過實際應用證明其學習速度和分類能力均優于BP網絡.

1 改進型RBF神經網絡

常規的RBF神經網絡是具有單隱層的三層前饋網絡,需先確定隱層節點個數,隱層節點一旦確定,網絡結構也就固定,其拓樸結構如圖1所示.RBF神經網絡的學習是通過改變隱層節點基函數中心向量和隱層至輸出層權值向量進行的.本文采用的改進型RBF神經網絡模型是基于最近鄰聚類學習算法的一種動態自適應RBF神經網絡模型[3],它是一種在線自適應聚類學習算法,不需事先確定隱層單元個數,此算法可在線學習.用該算法構造網絡的具體過程如下[4]:

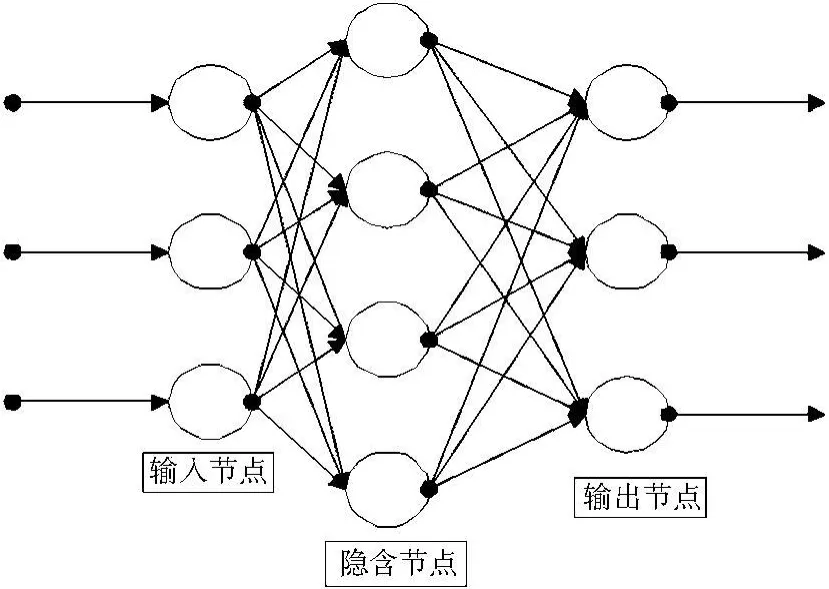
圖1 RBF神經網絡拓撲結構圖

設有N對輸入-輸出數據對(xk,yk),k=1,2,…,N,RBF神經網絡隱層非線性激勵函數取高斯函數,RBF網絡隱單元輸出為

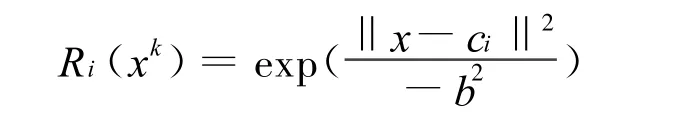
其中:xk是輸入矢量;yk是輸出:Ri(xk)是第i個隱單元的輸出;ci是第i個隱單元高斯基函數的中心矢量;b是高斯基函數的半徑.

1)定義S(l)用于存放屬于各類的輸出之和,定義計數器CT(l)用于統計屬于各類的樣本個數,其中l為類別數,選擇一個半徑b.

2)從第一個樣本對(x1,y1)開始,在x1上建立一個聚類中心,令c1=x1,S(1)=y1,CT(1)=1.這樣建立的RBF網絡只有一個隱單元,該隱單元的中心為c1,該隱單元到輸出層的權值為W1=S(1)/CT(1).

3)假設考慮第k個樣本數據對(xk,yk)時,k=3,4,…,N,設已存在n個聚類中心,其中心點分別為c1,c2,…,cn,網絡中已有n個隱單元.分別求出xk到這n個聚類中心的距離|xk-ci|,i=1,2,…,n,設|xk-cj|為這些距離中的最小距離,即cj為xk的最近鄰聚類,則:

如果|xk-ci|＞b,則將xk作為一個新聚類中心,并令cn+1=xk,S(n+1)=yk,CT(n+1)=1,且保持S(i),CT(i)的值不變.在上述建立的RBF網絡中再添加第n+1個隱單元,該隱單元到輸出層的權矢量為Wn+1=S(i)/CT(i).

如果|xk-ci|≤b,則S(j)=S(j)+yk,CT(j)=CT(j)+1.隱層到輸出層的權矢量為Wi=S(i)/CT(i).

4)根據上述規則建立的動態RBF神經網絡輸出為

由網絡結構的構造過程可見:高斯基函數半徑的大小決定了網絡的復雜程度.b越小,所得到的聚類數目就越多,從而導致非線性回歸過程越復雜,計算量也越大.但b是一個一維參數,一般可以通過實驗和誤差信息找到一個適當的值;由于每一個輸入-輸出數據對都可能產生一個新的聚類,因此構造出的網絡是一種動態網絡,實際上同時在進行參數和結構兩個過程的自適應調整.

2 改進型RBF神經網絡在旋轉機械故障診斷中的應用

2.1 學習樣本的建立

頻域轉子發生故障時的重要特征是機器伴有異常的振動和噪聲.振動信號對機器設備的運行狀態有直接的反映.尤其在頻域內,特征頻段上特征量的大小和比例關系可以反映出相應的故障類型.在BENT LY RK-4模擬轉子試驗臺上進行實驗研究,從測振傳感器提取出的時域連續振動信號,經A/D轉換、DFT(FF T)分析,得到振動信號的頻譜分析.本文以旋轉機械中常見的質量不平衡、轉子熱彎曲、軸向碰磨等8種故障作為網絡輸出,利用振動信號頻譜中的7個頻段上的不同頻率的譜峰能量值作為特征量,形成訓練樣本和樣本的目標輸出(見表1,表1中f為轉子的工作頻率).樣本的目標輸出中,1表示對應故障發生,0表示對應故障不發生.

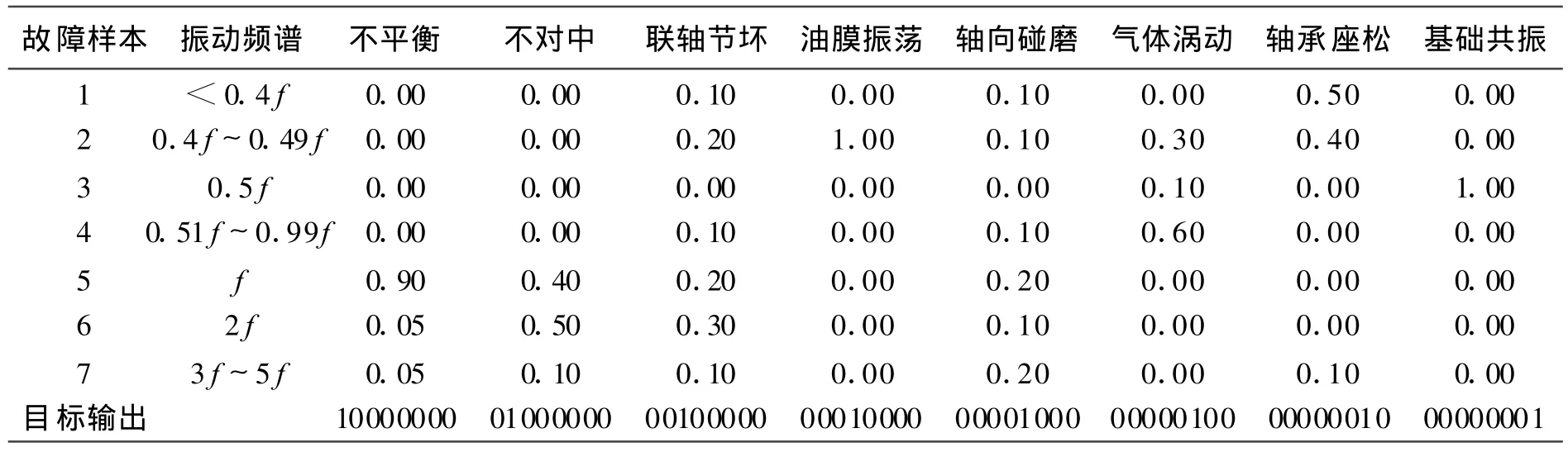
表1 旋轉機械常見故障標準模式特征向量

2.2 網絡結構的選取

由表1所列的學習樣本可知,輸入層選取7個節點;輸出層為綜合評價層,選擇了8個輸出層節點.

2.3 網絡學習性能分析

用表1所示學習樣本分別對具有相同結構的BP網絡和改進的RBF網絡進行訓練,訓練結果見表2.由表2可以看出,標準BP算法學習過程比較緩慢,而采用RBF網絡則學習過程非常快.

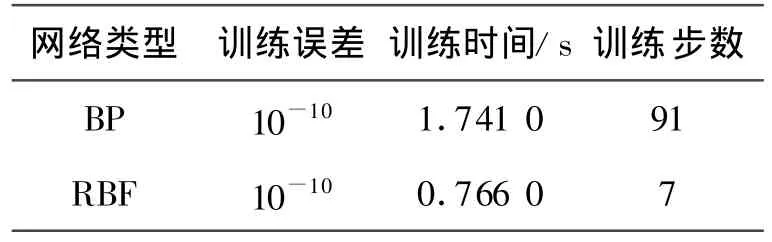
表2 網絡學習性能比較

2.4 網絡的測試

將待識別的故障樣本(見表3)作為網絡的輸入,輸入到上面已經訓練好的網絡中,經網絡非線性映射的輸出結果見表4.從表4可以看出,4個故障輸入模式分別對應第2、5、7、4個輸出節點的輸出值,分別接近于1,其它節點的輸出值均未超過0.3,可以分別診斷為不對中、軸向碰磨、軸承座松和油膜振蕩故障.可見網絡對待識別樣本進行了正確的分類,測試結果與實際發生的故障吻合.

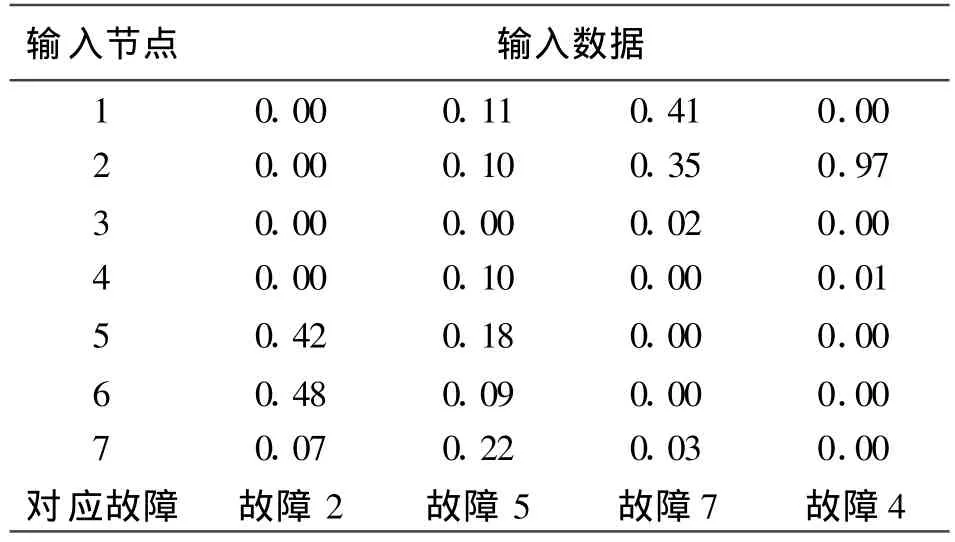
表3 待檢測故障模式特征向量

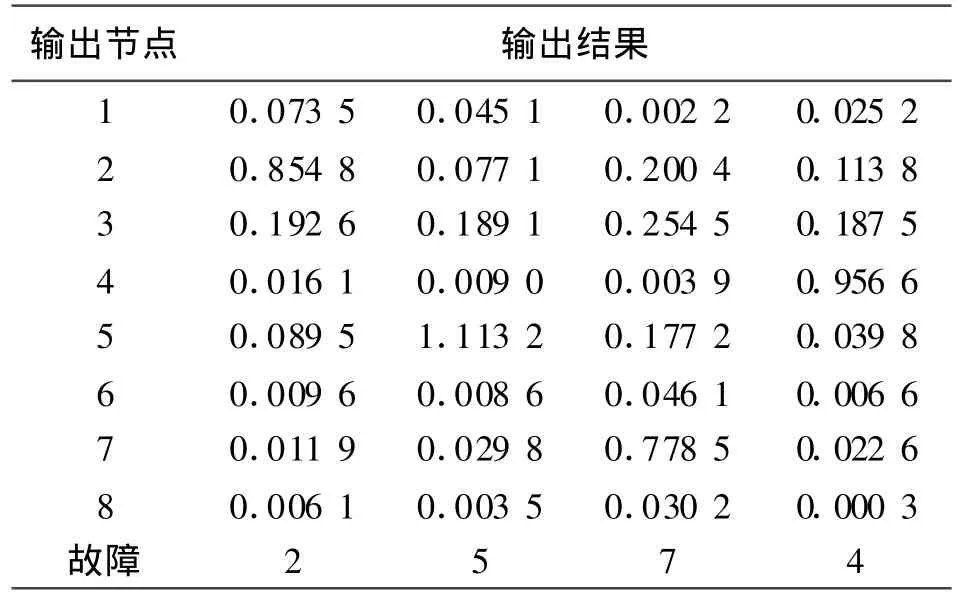
表4 網絡診斷結果

3 結束語

與目前廣泛應用的BP算法相比,改進型網絡學習算法從根本上避免了陷入局部極小點的問題,并且RBF網絡訓練速度非常快.旋轉機械故障診斷中的實際應用表明,改進型網絡能夠對旋轉機械各種復雜狀態做出判斷,具有良好的實用性.

[1]王偉.人工神經網絡——入門與應用[M].北京:北京航空航天大學出版社,1995.

[2]蘇高利.基于Matlab語言的BP神經網絡的改進算法[J].科技通報,2003,19(2):130-135.

[3]王立新.自適應模糊系統與控制——設計與穩定性分析[M].北京:國防工業大學出版社,1995.

[4]朱明星,張德龍.RBF網絡基函數中心選取算法的研究[J].安徽大學學報,2000,24(1):72-78.